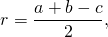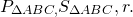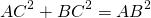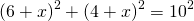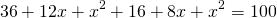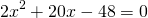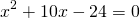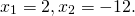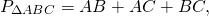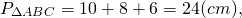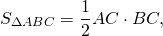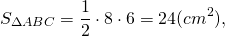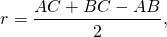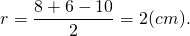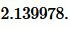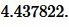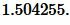Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами .
- Узнать ещё
- Окружность, вписанная в прямоугольный треугольник
- Как найти катеты через вписанную окружность
- Радиус вписанной окружности в прямоугольный треугольник онлайн
- 1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
- 2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
- 3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
- Треугольник вписанный в окружность
- Определение
- Формулы
- Радиус вписанной окружности в треугольник
- Радиус описанной окружности около треугольника
- Площадь треугольника
- Периметр треугольника
- Сторона треугольника
- Средняя линия треугольника
- Высота треугольника
- Свойства
- Доказательство
- Узнать ещё
- Окружность, вписанная в прямоугольный треугольник
- 📹 Видео
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где
– катеты,
– гипотенуза. Видеодоказательство
4. Площадь прямоугольного треугольника с катетами
:
5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты
и гипотенузу
следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус описанной окружности есть половина гипотенузы
:
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус вписанной окружности выражается через катеты
и гипотенузу
следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Узнать ещё
Знание — сила. Познавательная информация
Видео:Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

Окружность, вписанная в прямоугольный треугольник
Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.
Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле
где a и b — длины катетов, c — гипотенузы.
Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.
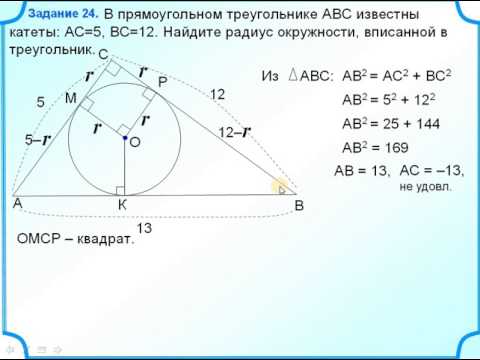
Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.

окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
1) По свойству отрезков касательных, проведенных из одной точки,

2) AB=AM+BM=6+4=10 см,
3) По теореме Пифагора:
Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.
Ответ: 24 см, 24 см², 2 см.
Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.

окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
1) Проведем отрезки OK и OF.
(как радиусы, проведенные в точки касания).
Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).
А так как OK=OF (как радиусы), то OKCF — квадрат.
2) По свойству касательных, проведенных из одной точки,
3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.
Видео:Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

Как найти катеты через вписанную окружность
Видео:Задание 24 Радиус окружности вписанной в прямоугольный треугольникСкачать
Радиус вписанной окружности в прямоугольный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в прямоугольный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
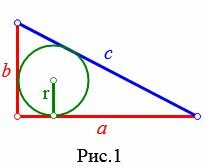 |
Радиус вписанной в треугольник окружности, если известна площадь треугольника S и полупериметр p вычисляется из следующей формулы (статья Радиус вписанной в треугольник окружности, формула (5)):
| ( small r= frac , ) | (1) |
| ( small p= frac . ) | (2) |
Площадь прямоугольного треугольника по катетам вычисляется из формулы:
| ( small S= large frac small cdot a cdot b. ) | (3) |
Подставляя (2) и (3) в (1) получим формулу вписанной в прямоугольный треугольник окружности:
| ( small r= large frac ab> (a+b+c)> ) ( small = large frac, ) | (4) |
| ( small c= sqrt . ) | (5) |
Из формулы (4) выведем другую эквивалентную формулу. Умножим числитель и знаменатель формулы (4) на ( small a+b-c ):
| ( small r= frac ) ( small = frac ) ( small = frac ) | (6) |
Учитывая (5), формулу (6) можно переписать так:
| ( small r= frac ) ( small = frac .) |
Таким образом другая формула вычисления радиуса вписанной в треугольник окружности имеет вид:
| ( small r= frac ,) | (7) |
где c вычисляется из (5).
Пример 1. Известны катеты прямоугольного треугольника a=17 и b=5. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (4) и (7). Вычислим, сначала, гипотенузу прямоугольного треугольника из формулы (5):
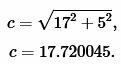 |
Подставим значения ( small a=17, ; b=5; c=17.720045 ) в (7):
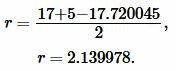 |
Ответ:
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
Пусть известны катет a прямоугольного треугольника и прилежащий к нему угол β(Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
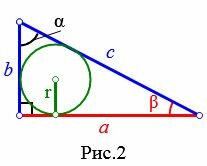 |
| ( small frac =frac .) |
Учитывая, что ( small alpha=90°-beta ) и ( small sin (90°-beta)=cos beta ), получим:
| ( small frac =frac ) ( small =frac =frac .) | (8) |
Тогда из (8) получим:
| ( small b=frac . ) | (9) |
Далее, из теоремы синусов:
| ( small frac =frac ) ( small =frac =frac .) |
| ( small c=frac .) | (10) |
Чтобы получить формулу радиуса вписанной в прямоугольный треугольник окружности через катет и прилежащий к нему угол, подставим значения ( small b ) и ( small c ) из (9) и (10) в (7):
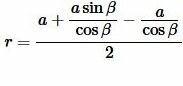 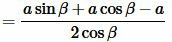 |
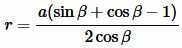 | (11) |
Пример 2. Известны катет ( small a=21 ) и прилежащий к нему угол ( small beta=30° ) прямоугольного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Подставим значения ( small a=21 ) ( small beta=30° ) в (11):
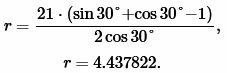 |
Ответ:
Видео:Важная формула для ЕГЭ! Радиус вписанной окружности для прямоугольного треугольникаСкачать
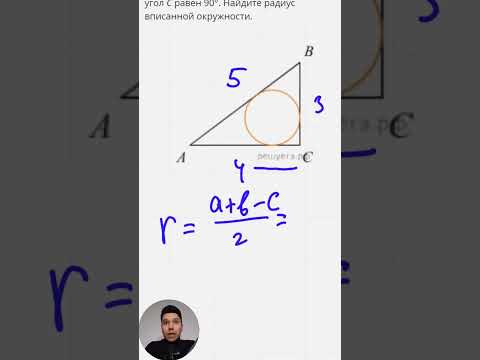
3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
Пусть известны катет a прямоугольного треугольника и противолежащий угол ( small alpha; ) (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
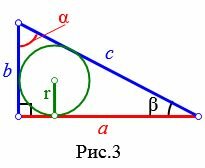 |
В предыдущем параграфе мы вывели формулу вписанной в прямоугольный треугольник окружности по катету и прилежащему углу (формула (11)). Учитывая, что в прямоугольном треугольнике сумма острых углов равна 90°, имеем:
| ( small alpha+beta=90°) ( small beta=90°-alpha ) |
Тогда (11) можно преобразовать так (подробнее на странице Формулы приведения тригонометрических функций:
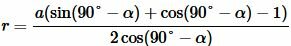 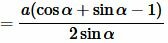 |
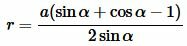 | (12) |
Пример 3. Известны катет ( small a=6 ) прямоугольного треугольника и противолежащий угол ( small alpha=53°. ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (12). Подставим значение ( small a=6, ; alpha=53° ) в (12):
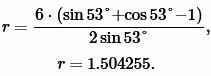 |
Ответ:
Видео:Геометрия Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружностиСкачать
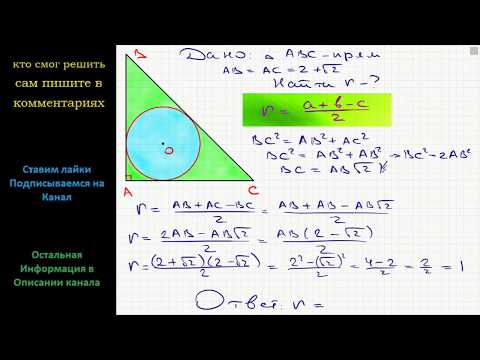
Треугольник вписанный в окружность
Видео:ЕГЭ задание 16 Радиус вписанной окружности прямоугольного треугольника. Разные способы решенияСкачать

Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Видео:Радиус описанной окружностиСкачать

Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Видео:Найти расстояние между центрами описанной и вписанной окружностей в прямоугольном треугольникеСкачать
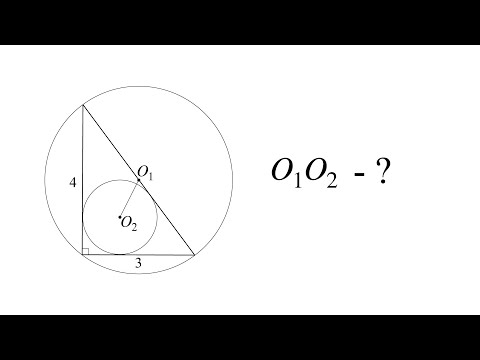
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Видео:Задача № 27933 ЕГЭ по математике. Урок 147Скачать

Узнать ещё
Знание — сила. Познавательная информация
Видео:Окружность, вписанная в прямоугольный треугольник | Геометрия 8-9 классыСкачать

Окружность, вписанная в прямоугольный треугольник
Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.
Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле
где a и b — длины катетов, c — гипотенузы.
Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.
Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.

окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
1) По свойству отрезков касательных, проведенных из одной точки,

2) AB=AM+BM=6+4=10 см,
3) По теореме Пифагора:
Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.
Ответ: 24 см, 24 см², 2 см.
Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.

окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
1) Проведем отрезки OK и OF.
(как радиусы, проведенные в точки касания).
Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).
А так как OK=OF (как радиусы), то OKCF — квадрат.
2) По свойству касательных, проведенных из одной точки,
3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.
📹 Видео
Окружность вписанная в треугольник и описанная около треугольника.Скачать

Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Нахождение радиуса вписанной окружности в прямоугольном треугольникеСкачать

🔴 Радиус вписанной в прямоугольный треугольник ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать

Найдите гипотенузуСкачать