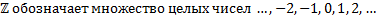На какие классы разбивается множество точек плоскости при помощи окружности

4. На какие классы разбивается множество точек плоскости при помощи : а) окружности ; б) круга ; в) прямой?

НАВЕРНОЕ ПО ЛОГИКЕ.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

На сколько частей разбивают плоскость две пересекающиеся прямые?

На сколько частей разбивают плоскость две пересекающиеся прямые?

Видео:Уравнение окружности (1)Скачать

Рассмотри чертеж и запиши обозначения точек лежащих на окружности принадлежащих кругу лежащих вне окружности не принадлежащих кругу внутри?

Рассмотри чертеж и запиши обозначения точек лежащих на окружности принадлежащих кругу лежащих вне окружности не принадлежащих кругу внутри.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Сколько точек в пересечении : а)прямой и окружности , б)двух окружностей?

Сколько точек в пересечении : а)прямой и окружности , б)двух окружностей.

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

На какое наибольшее число различных частей могут разбивать плоскость три окружности?

На какое наибольшее число различных частей могут разбивать плоскость три окружности.

Видео:Уравнение плоскости. 11 класс.Скачать

В каком случае множество А называют множество B?

В каком случае множество А называют множество B?

Проиллюстрируйте это понятие с помощью кругов Эйлера.

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

В каком случае множество А называют подмножеством множества В?

В каком случае множество А называют подмножеством множества В?

Проиллюстрируйте это понятие с помощью кругов Эйлера

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

На сколько частей разбивают плоскость две пересекающиеся прямые?

На сколько частей разбивают плоскость две пересекающиеся прямые?

Видео:Множества на комплексной плоскости. Связное множество. Односвязная область. Граница. Круг сходимостиСкачать

Сколько точек пересечения могут иметь прямая окружностью?

Сколько точек пересечения могут иметь прямая окружностью?

Объясни с помощью черчежа.

Видео:Уравнение окружностиСкачать

На сколько частей разбивают плоскость 2 прямые?

На сколько частей разбивают плоскость 2 прямые.

Видео:9 класс, 2 урок, Множества и операции над нимиСкачать

Начертите три пересекающиеся прямые на плоскости?

Начертите три пересекающиеся прямые на плоскости.

На какое наибольшее число частей могут разбивать плоскость эти прямые?

На этой странице сайта размещен вопрос 4. На какие классы разбивается множество точек плоскости при помощи : а) окружности ; б) круга ; в) прямой? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников студенческий. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Полуплоскости, круги и другие множества на плокости

Множества

После проработки этой главы Вы должны уметь:

а) использовать систему записи множеств;

б) определять, равны ли данные два множества или является ли одно из данных множеств подмножеством другого;

в) находить объединение, пересечение и разность двух данных множеств.

Что такое множество?

В математике часто рассматриваются наборы объектов различных типов. Например, можно рассматривать:

· решения квадратного уравнения;

· точки на окружности;

· простые числа меньше 100;

· область определения вещественной функции.

Понятие множества предоставляет единую структуру, необходимую для систематического рассмотрения подобных наборов.

Множествоможно рассматривать как набор объектов, таких как числа, точки, функции или даже другие множества. Каждый объект в множестве называется его элементом;элементы принадлежатмножеству.

Ограничений на типы объектов, которые могут находиться в множестве, нет при условии, что множество задано таким образом, что мы, в принципе, можем определить, принадлежит ли данный элемент множеству.

Такое описание может быть произведено многими способами. Например, можно определить множество S как множество чисел из списка 4, 9, 3, 2. Это описание позволяет определить, что, к примеру, число 2 принадлежит S, а число 1 — нет. Такое множество может быть проиллюстрировано схемой, как на полях; она называется диаграммой Веннав честь жившего в XIX веке кембриджского математика Джона Венна.

Также множество E может быть задано утверждением: «пусть E будет множеством всех чётных целых чисел». Такое описание позволяет нам определить, является ли данный объект элементом E, узнав, является ли он чётным целым числом; например, 6 принадлежит E, а 5 — нет.

Некоторые множества используются так часто, что для их записи заняты специальные символы.

Мы используем символ ∈, чтобы показать принадлежность множеству; например, чтобы показать, что 7 — это элемент ℕ, мы пишем:

.

Чтобы показать, что 9 — это не элемент ℕ, мы пишем:

.

Также символ ∈ используется, чтобы ввести символ, обозначающий произвольный элемент множества. Например, пишут

чтобы показать, что x — это произвольный (неопределённый) элемент множества ℝ. Иногда говорят, что x — это вещественная переменная. Вообще переменная — это символ (типа x или n), который обозначает произвольный элемент множества.

Упражнение 1.1

Система записи множеств

Теперь изучим некоторые формальные способы записи множеств.

Множество с небольшим количеством элементов может быть задано перечисление этих элементов в фигурных скобках. Например, можно задать множество A, состоящее из первых пяти натуральных чисел, так:

Принадлежность множеству не зависит от порядка, в котором перечислены его элементы, поэтому множество A может быть с тем же успехом задано так:

Таким же образом можно задать множество B вершин квадрата, показанного на полях:

Можно даже задать множество C, элементами которого будут три множества , и :

Множество из одного элемента, как, например, , называется одноэлементным, или одноточечным. (Не путайте множество и число 2.)

Упражнение 1.2

Не имеет значения, указываем ли мы элемент множества в фигурных скобках несколько раз: мы по-прежнему описываем множество, состоящее из каждого из элементов по отдельности. Например, и — это одно и то же множество. Тем не менее, записи одного элемента несколько раз обычно избегают.

В случае множеств с большим числом элементов перечислять все элементы непрактично, поэтому иногда для указания на продолжение определённой модели принадлежности элементов множеству используются три точки (называемые многоточием, или эллипсисом). Например, множество первых 100 натуральных чисел можно задать, написав .

Использование многоточия может быть расширено и на некоторые бесконечные множества. Например, множество всех натуральных чисел натуральных чисел может быть записано как . Недостаток такой записи заключается в том, что модель, обозначенная многоточием, может быть двусмысленной. Например, непонятно, какое множество описывает запись : множество всех нечётных простых чисел или множество всех нечётных чисел больше единицы. По этой причине такая запись может быть использована, только когда модель принадлежности очевидна или когда даются дополнительные пояснения.

Другой способ задания множества — это использование переменных для построения объектов необходимого типа и последующая запись условий, которым должны отвечать эти объекты. Например, рассмотрим интервал (3, ∞), которые состоит из всех такие действительных чисел x, что x > 3. Используя систему записи множеств, мы можем записать его как

что читается так: множество действительных x таких, что x больше 3.

Часто с помощью такой записи множество может быть описано несколькими разными способами. В частности, для обозначения произвольного элемента множества может быть использована другая буква:

Если после двоеточия нужно поставить больше одного условия, то они разделяются запятой или словом «и». Так, полуинтервал (0, 1] может быть записан так:

хотя обычно эти неравенства совмещают и пишут

Иногда удобно задать множество, написав перед двоеточием выражение от одной или нескольких переменных, а после — условия, накладываемые на переменные. Например, множество чётные целых чисел меньше 100 может быть задано так:

Так же, как и при записи множества как списка элементов, запись одного элемента несколько раз значения не имеет. Например, записи

задают одно и то же множество.

Запись множеств полезна, когда нам нужно указать множество решенийодного или нескольких уравнений. Например, решения уравнения составляют множество

Множество решений уравнений зависит от множества значений, из которого выбираются решения. Например, множество решений уравнения

—

если нас интересуют действительные решения, но если мы рассматриваем только целые решения, то это будет

В этой части книги мы полагаем, что решения берутся из , если не оговорено иное.

Иногда у уравнения нет действительных решений, поэтому в множестве его решений нет элементов. Такое множество называется пустым множествоми обозначается символом ⌀. Например,

Пример 1.1

Решение

Упражнение 1.3

1.3 Множества на плоскости

В части I1 Вы познакомились с плоскостью и увидели, что любая точка на плоскости может быть представлена как упорядоченная пара по отношению к данной паре осей. Множество точек из называется множеством на плоскости,или плоской фигурой. Простые примеры множеств на плоскости — это прямые и окружности.

Прямые

Рассмотрим прямую линию l c наклоном a и пересечением с осью ординат на расстоянии b от начала координат. Эта прямая — это набор всех таких точек плоскости , что . Используя систему записи множеств, запишем это так:

.

(Иногда в качестве краткой записи этого множества используется фраза «прямая ».)

Прямую, параллельную к оси Oy и отстоящую от неё на расстояние c, записывают так:

.

Упражнение 1.4

Окружности

Единичная окружностьU — это множество точек плоскости , расстояние от которых до точки начала координат равно 1. По теореме Пифагора, это точки , удовлетворяющие уравнению , так что единичная окружность записывается так:

.

В общем случае окружность C c радиусом r и центром в точке — это множество точек , лежащих от точки на расстоянии r. По теореме Пифагора, это точки , удовлетворяющие уравнению , так что единичная окружность записывается так:

.

Упражнение 1.5

Полуплоскости, круги и другие множества на плокости

.

Эта прямая делит на три разные части: саму линию l, множество H₁ точек, лежащих над прямой, и множество H₂ точек, лежащих под прямой.

Рассмотрим произвольную точку из H₁, как показано на полях. Точка лежит на прямой l под P, как показано на рисунке, так что y > 1 – x. Аналогично, для любой точки из H₂ выполняется y

Видео:Множества и операции над нимиСкачать

ПРАКТИЧЕСКАЯ РАБОТА 3. РАЗБИЕНИЕ МНОЖЕСТВА НА КЛАССЫ

Цель. Рассмотреть правила разбиения множества на классы, уметь решать задачи на классификацию, освоить математическую символику связанную с этими понятиями. Уметь привести примеры на использование понятия классификации из начального курса математики.

Теоретическая часть

Вопросы к изучению

1. Понятие разбиения множества на классы.

2. Некоторые задачи, связанные с операциями над конечными множествами.

Ø дихотомическая классификация.

Обозначения

n (A) — число элементов конечного множества А.

Правила

· Разбиения множества на классы;

· Нахождения числа элементов в объединении конечных множеств:

n (А ÈВ) = n (А) + n (В) – n (AÈB);

n (А ÈВ) = n (А) + n (В), если (А Ç B ) = Æ.

Практическая часть

1. Выделите из множества К= два подмножества. В одно включите числа, кратные 2, а в другое – кратные 3. Произошло ли разбиение множества К на класс чисел, кратных 2, и класс чисел, кратных 3? Можно ли разбить данное множество К на три класса: К₁= , К₂= , К₃= ?

2. Определите классы разбиения множества Х четырехугольников, если оно осуществляется при помощи: 1) свойства «быть прямоугольником»; 2) свойств «быть прямоугольником» и «быть ромбом»; 3) свойств «быть прямоугольником» и «быть квадратом»; 4) свойств «быть прямоугольником» и «быть трапецией».

3. Из множества натуральных чисел выделите подмножество чисел, кратных 8. На сколько классов при этом произошло разбиение множества натуральных чисел? Изобразите полученные классы при помощи кругов Эйлера и назовите по два представителя из каждого класса.

4. На какие классы разбивается множество точек плоскости при помощи: а) окружности; б) круга; в) прямой?

5. На множестве натуральных чисел рассматривается свойство «быть кратным 7». Сколько классов разбиения множества N оно определяет? Назовите по два элемента из каждого класса.

6. Из множества четырехугольников выделили подмножество фигур с попарно параллельными сторонами. На какие классы разбивается множество четырехугольников с помощью свойства «иметь попарно параллельные стороны»? Начертите по два четырехугольника из каждого класса.

7. Изобразите при помощи кругов Эйлера множество N натуральных чисел и его подмножества: четных чисел и чисел кратных 7. Можно ли утверждать, что множество N разбито: а) на два класса: четных чисел и чисел, кратных 7; б) на четыре класса: четных чисел, кратных 7; в) нечетных чисел, не кратных 7; г) четных чисел не кратных 7; д) нечетных чисел, кратных 7.

8. На множестве четырехугольников рассматриваются два свойства: «быть прямоугольником» и «быть квадратом». На какие классы разобьется множество четырехугольников при помощи этих свойств? Начертите по два четырехугольника из каждого класса.

9. Изменится ли ответ в предыдущем упражнении, если на множестве четырехугольников рассмотреть свойства: а) «быть прямоугольником» и «быть ромбом»; б) «быть прямоугольником» и «быть трапецией»?

10. Можно ли узнать, сколько человек в классе, если в нем: 1) 17 мальчиков и 15 девочек; 2) 17 мальчиков и 23 спортсмена?

11. Из 50 учащихся 37 изучают английский язык, 17- немецкий. Сколько человек изучают оба языка?

1. Придумайте три примера известных вам классификаций из нематематических наук

2. Из 32 школьников 12 занимаются в волейбольной секции, 15 – в баскетбольной, 8 человек занимаются и в той и в другой секции. Сколько школьников не занимаются ни в волейбольной, ни в баскетбольной секции?

3. В делегации 6 человек, знающих французский или немецкий язык. Трое из них говорят только на французском, двое – только на немецком. Сколько человек говорят на двух языках – французском и немецком?

4. Из 100 студентов английский язык изучают 28 человека, немецкий – 30 человек, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 15. Все три языка изучают 3 учащихся. Сколько студентов изучают только один язык? Сколько студентов не изучают ни одного языка?

5. В школе 70 учеников. Из них 27 ходит в драмкружок, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов. 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не ходят в драмкружок?

6. Докажите, что если п – число свойств, с помощью которых множество разбивается на максимальное число классов, то число этих классов равно 2 п

ТЕМА 5. ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ (ЛЕКЦИЯ)

1. Декартово произведение множеств

2. Свойства операции декартова произведения

3. Кортеж. Длина кортежа

ТЕМА 5.1. НЕКОТОРЫЕ ЗАДАЧИ, СВЯЗАННЫЕ С ДЕКАРТОВЫМ ПРОИЗВЕДЕНИЕМ МНОЖЕСТВ (С/Р)

1. Число элементов в объединении и разности конечных множеств

2. Число элементов в декартовом произведении конечных множеств

ПРАКТИЧЕСКАЯ РАБОТА 4. ДЕКАРТОВО ПРОИЗВЕДЕНИЕ

Цель. Уметь решать практические задачи на понятие декартова произведения и его свойств.

Теоретическая часть

Вопросы к изучению

1. Декартово произведение множеств

2. Свойства операции декартова произведения

3. Кортеж. Длина кортежа

Ø декартово произведение множеств;

Ø длина кортежа

Обозначения

А ´ В = — запись определения декартова произведения множеств А и В.

Ø Операции над множествами: объединение, пересечение, вычитание, декартово произведение.

Ø Свойства этих операций:

· дистрибутивность декартова произведения относительно объединения и вычитания множеств, т.е. для любых множеств А, В и С выполняются равенства: (AÈB) ´ С = (A ´ С) È (B ´ С), (A B) ´ С = (A ´ С) (B ´ С).

Правила

Ø Нахождения числа элементов в декартовом произведении конечных множеств: n (А ´ В) = n (А) × n (В).

Практическая часть

1. Элементами множеств А и В являются пары чисел: А = , В = . Найдите пересечение и объединение данных множеств.

2. Запишите различные двузначные числа, используя цифры 3, 4 и 5. Сколько среди них таких, запись которых начинается с цифры 3? Как связано решение данной задачи с понятием декартова произведения множеств?

3. Перечислите элементы декартова произведения A ´ В, если: а) А = , B = ; б) А = В = ; в) А = , В = Æ.

4. Даны множества А = и В = . Перечислите элементы множеств A ´ В и В ´ А. Верно ли, что: а) Множества A ´ В и В ´ А содержат одинаковое число элементов; б) Множества A ´ В и В ´ А равны?

5. Проверьте справедливость равенства (AÈB) ´ С = (A ´ С) È (B ´ С) для множеств А = , В = , С = . Выполняется ли для них равенство (A B) ´ С = (A ´ С) (B ´ С) ?

6. Сколько букв в слове «барабан»? Сколько различных букв в этом слове? Сформулируйте эту задачу, используя понятия множества и кортежа.

7. Чем отличается множество цифр в записи числа 56576 от кортежа цифр в его записи?

8. Изобразите в прямоугольной системе координат множество A ´ В, если: а) А = [-2; 2]. В = ; б) А = [-2; 2]. В = (2, 4); в) А = R, В = [2; 4].

1. Изобразите на декартовой плоскости множество [ 0; 1) ´ (0,1); ´ [ 0; 1); [ 0; 1) ´ R; N ´ R; N ´ ; ´ N; ´ R.

2. В звене 7 мальчиков и 6 девочек. Сколькими способами можно выбрать пару учеников, состоящую из мальчика и девочки, для дежурства по классу?

3. В каких случаях А´В = В´А?

4. Составьте таблицу результатов однокругового шахматного турнира трех: Иванова, Петрова, Сидорова (результаты возьмите произвольно).

5. Фабрика верхнего трикотажа изготовляет мужские пуловеры, женские костюмы, кофты и платья следующих расцветок: бордовая, синяя, голубая, зеленая, коричневая, серая. Составьте таблицу, иллюстрирующую декартово произведение множества изделий и множества цветов, и заполните ее.

6. Решите следующие задачи, построив дерево возможных вариантов: А) у продавца имеется три варианта мороженного: клубничное, сливочное и ореховое. Наташа и Катя решили купить по одной порции. Сколько существует вариантов такой покупки? Б) Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

📽️ Видео

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

1 2 4 сопряжение окружностейСкачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрическая вероятностьСкачать

Как найти множество точек комплексной плоскости?Скачать

Уравнение окружности. Практика. Урок 7. Геометрия 9 классСкачать