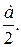В трапеции АBCD угол BAD прямой. Окружность, построенная на большем основании АD как на диаметре, пересекает меньшее основание BC в точке C и M.
а) Докажите, что угол BАM равен углу CАD.
б) Диагонали трапеции АBCD пересекаются в точке O.
Найдите площадь треугольника АOB, если АB = 6, а BC = 4BM.
а) Трапеция AMCD вписана в окружность, тогда углы CAD и MDA равны. Так как углы CAD и BAM равны половине дуги AM, то они равны между собой, что и требовалось доказать.
б) откуда
тогда
а
Так как треугольники AOD и COB подобны, то
тогда
Ответ: б)
| Критерии оценивания выполнения задания | Баллы | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 | |||||||||
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 | |||||||||
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Видео:Построить трапецию по диагоналям и основаниям.Скачать  III.3. Задачи к теоретической карте № 3№ 1.
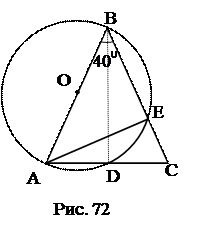
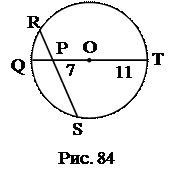
№2.Биссектриса угла В треугольника АВС пресекает описанную окружность в точке D. Доказать, что треугольник АDC равнобедренный. 1. 2. Используемые факты из теоретической карты: 1.2. №3.Доказать, что сторона треугольника, лежащая против угла в 30 0 , равна радиусу окружности, описанной около треугольника. 1. 2. Вид 3. Используемые факты из теоретической карты: №4. Угол при вершине равнобедренного треугольника равен 40°. Одна из 1. BD 2. 3. 4. Ответ: 40 0 , 40 0 , 100 0 Используемые факты из теоретической карты: 1.2. №5. Через вершины Ви С треугольника АВС проходит окружность, пересекающая стороны АВ и АС в точках К и М соответственно. Доказать, что ∆АВС ∆АМК. Найти МК и АМ, если АВ=2, ВС=4, АС=5, АК=1. 1. Проведем 2. 3. 4. 5. 6. МК. 7. АМ. Ответ: Используемые факты из теоретической карты: 1.2.№6. Окружность, построенная на стороне параллелограмма как на диаметре, проходит через середину соседней стороны и точку пересечения диагоналей. Найти углы параллелограмма. 1. 2. 3. 4. Ответ: 60 0 , 120 0 . Используемые факты из теоретической карты: 1.2. №7. Окружность, построенная на большем основании трапеции как на диаметре, касается меньшего основания и пересекает боковые стороны, деля их пополам. Найти меньшее основание трапеции, если радиус окружности равен R. проведем АЕ, 1. 2. 3. CP = R, PD = R – OP. 4. ∆CPD: OP 2 + 2R∙OP – 2R 2 =0, 5. Трапеция ABCD – равнобедренная. ВС = 2ОР. Ответ: Используемые факты из теоретической карты: 1.2. №8. Высоты остроугольного треугольника продлены до пересечения с описанной окружностью. Доказать, что отрезки этих линий от ортоцентра до окружности делятся соответственными сторонами пополам. Точка К – ортоцентр треугольника АВС. 1. ∆ВНС: 2. ∆АРС: 3. 4. Аналогично доказывается, что Используемые факты из теоретической карты: 1.2. №9.Окружность разделена точками A, B, C и D так, что 1. 2. 3. Используемые факты из теоретической карты: 1.3. №10. На окружности взяты четыре точки. Середины образованных дуг попарно соединены отрезками. Доказать, что среди этих отрезков есть, по крайней мере, два перпендикулярных. 1. Выразить 2. Используемые факты из теоретической карты: 1.4. №11. В окружность вписан четырехугольник. Его противоположные стороны CD и АВ, ВС и AD продолжены до взаимного пересечения в точках N и F. Доказать, что биссектрисы углов BFA и AND перпендикулярны. 1. 2. 3. 4. 5. 6. 7. Используемые факты из теоретической карты: №12. Через точку касания двух окружностей проведены две секущие, концы которых соединены хордами. Доказать, что эти хорды параллельны. 2. 3. Используемые факты из теоретической карты: 1.2; 1.5. №13.В треугольнике АВС проведены высоты ВВ1 и СС1. Доказать, что Используемые факты из теоретической карты: 1.5. №14. Окружность проходит через вершины В, С, D трапеции ABCD и касается боковой стороны АВ в точке В. Основания трапеции а и b. Найти диагональ BD. 2. 3. 4. 5. Используемые факты из теоретической карты: 1.2; 1.5. №15. Из точки С окружности на хорду АВ опущен перпендикуляр CD. Из концов хорды опущены перпендикуляры АЕ и BF на касательную к окружности в точке С. Доказать, что 1. 2. 4. 5. Используемые факты из теоретической карты: 1.2; 1.5. №16. Дана точка Р, удаленная на 7 см от центра окружности радиуса 11 см. 2. 3. 4. 5. Ответ: 6 и 12. Используемые факты из теоретической карты: 2.1. №17. АС и ВD – диагонали ромба АВCD. Окружность описанная около 1. АО 2 +ОВ 2 =АВ 2 . 2. АО∙ОЕ=ОВ 2 , АО∙(АО – ЕС) = ОВ 2 . 3. Решить систему уравнений Ответ: 32 см, 24 см. Используемые факты из теоретической карты: 2.1. № 18.Через точку Р диаметра АВ данной окружности проведена хорда CD, образующая с диаметром АВ угол 60°. Вычислить радиус окружности R, если 1.СК. 2. КР. 3. ОР ( 4. Выразить АР через ОР и R. 5. Выразить РВ через ОР и R. 6.Составить равенство АР·РВ = СР·РD. 7.Выразить R из составленного равенства. Ответ: Используемые факты из теоретической карты: 2.1; №19. Из внешней точки проведена к окружности секущая длиной 12 см и Определить длину касательной. 1. Выразить AD через АС и DС. 2. Выразить АВ через DС. 3. Составить уравнение.
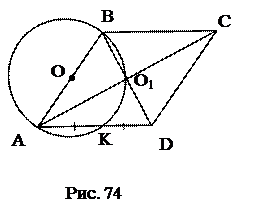
4. DС. 5. АВ. Ответ: Используемые факты из теоретической карты: 2.2. №20. Полуокружность, построенная на меньшем катете, как на диаметре, делит биссектрису острого угла, прилежащего к этому катету, в отношении 1:3. Найти углы треугольника. 1. КС – касательная, КВ – секущая, выразить КС (в частях). 2. sin 3. Используемые факты из теоретической карты: 2.2. №21. Катеты прямоугольного треугольника равны а и b. На отрезках гипотенузы, определенных основанием перпендикуляра, опущенного на гипотенузу из 1. 2. КС (СD – касательная, СА – секущая). 4. Аналогично LB. Ответ: №22. На боковой стороне АВ равнобедренного треугольника как на диаметре построена окружность. Окружность пересекает основание АС в точке М, а План решения. 1. 2. 3. Ответ: Используемые факты из теоретической карты: 1.2; 2.3. Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать  Окружность, построенная на основании ВС трапеции ABCD как на диаметре, проходит через середины диагоналей АС и BD трапеции и касаетсяВидео:Геометрия В окружность вписана трапеция, диагональ которой делит угол при большем основании пополамСкачать  Ваш ответВидео:Всё про углы в окружности. Геометрия | МатематикаСкачать  решение вопросаВидео:Задача про трапецию, описанную около окружностиСкачать  Похожие вопросы
Популярное на сайте: Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так. Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 📹 ВидеоПостроить трапецию по основаниям и двум сторонамСкачать  Трапеция. Практическая часть - решение задачи. 8 класс.Скачать  Где центр окружности? ТрапецияСкачать  Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать  Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать  ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать  Г: Найдите диагональ и боковую сторону равнобедренной трапеции с основаниями 20 и 12 см, еслиСкачать  Математика 11, задача по геометрии, 2-я часть ЕГЭ, задача 16Скачать  Основательная трапеция. Математика. Геометрия 11 класс.Скачать 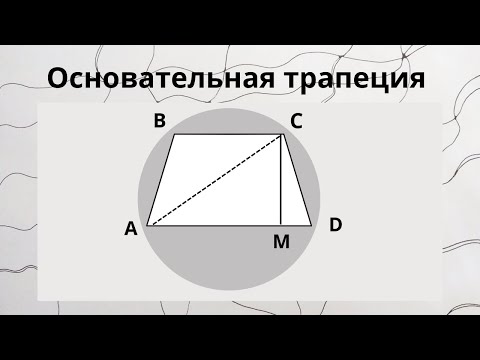 Касательные к окружности | Задачи 11-20 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать  Вписанные и описанные окружности. Вебинар | МатематикаСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  8 класс, 6 урок, ТрапецияСкачать  Окружность, вписанная в трапециюСкачать  В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. окружность проходит через точки C,DСкачать  |
 1.
1.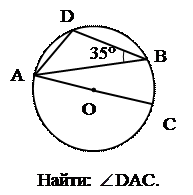 2.
2. 3.
3. 4.
4. АDВ .
АDВ .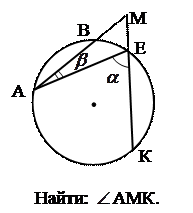 5.
5.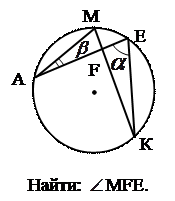 6.
6.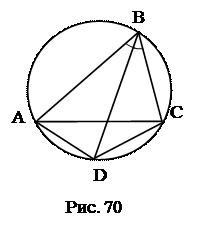 План доказательства.
План доказательства.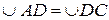 (доказать).
(доказать).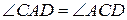 .
.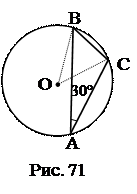 План доказательства.
План доказательства.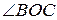 .
.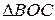 .
.
 План решения.
План решения. АС.
АС.

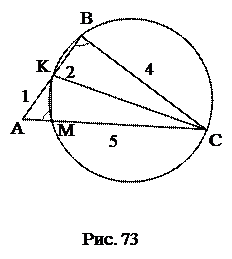 План доказательства.
План доказательства. .
.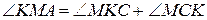 .
.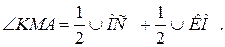
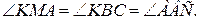
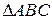
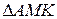 .
.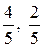 .
. План решения.
План решения.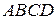 – ромб
– ромб – равносторонний.
– равносторонний. .
. .
. План решения.
План решения.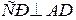 .
.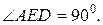
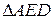
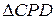 : СD 2 = 4R(R — ОР).
: СD 2 = 4R(R — ОР).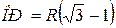 .
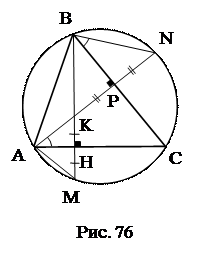
.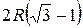 .
.
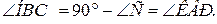
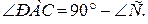
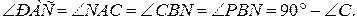
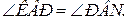 5.
5. 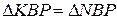 . 6. КР=PN.
. 6. КР=PN.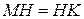 .
.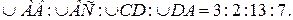 Хорды
Хорды 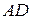 и
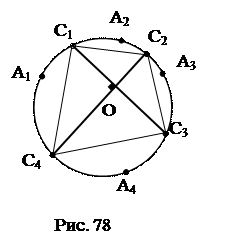
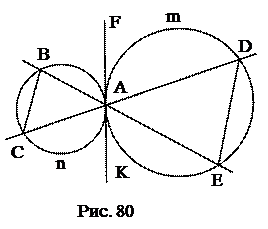
и 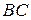 продолжены до пересечения в точке М. Найти угол АМВ.
продолжены до пересечения в точке М. Найти угол АМВ.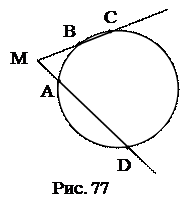
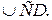
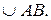
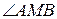 .
.
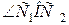 через
через  и
и 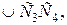 а затем через дуги
а затем через дуги 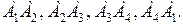
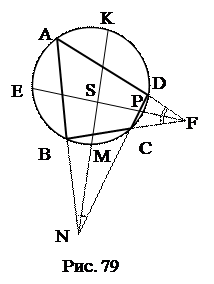
 .
.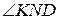 .
.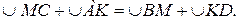
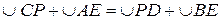 .
.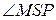 .
. .
. 1.
1.  .
. .
. .
. План решения.
План решения.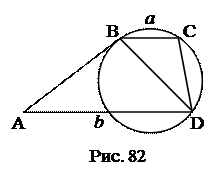 1.
1. 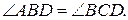
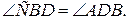
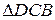 .
.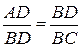 .
.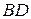 . Ответ:
. Ответ: 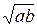 .
.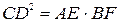 .
.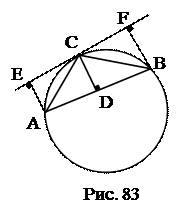 План доказательства.
План доказательства.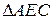

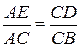 .
.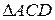
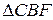 .
.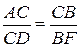 . 6. BF. 7.
. 6. BF. 7. 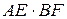 .
. 1.
1.  .
.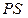 ∙
∙ 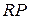 =
= 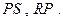
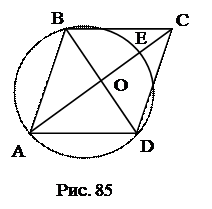 План решения.
План решения.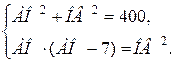
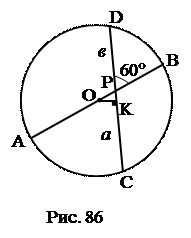 Дополнительное построение: ОК ^ DC.
Дополнительное построение: ОК ^ DC.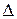 ОКР).
ОКР).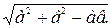
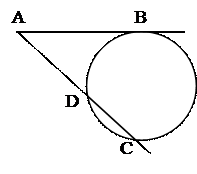 План решения.
План решения.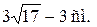
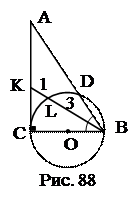 План решения.
План решения.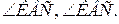
 Ответ: 30 0 , 60 0 .
Ответ: 30 0 , 60 0 .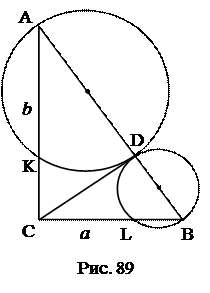 План решения.
План решения.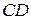 .
. . Используемые факты из теоретической карты: 2.2.
. Используемые факты из теоретической карты: 2.2.
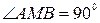 .
.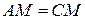 .
. .
. ,
,