Может ли прямая перпендикулярная к плоскости быть параллельна прямой лежащей в этой плоскости да нет (6 видео)

Перпендикулярность прямых и плоскостей

Содержание

Перпендикулярные прямые
Перпендикулярность прямой и плоскости
Признак перпендикулярности прямой и плоскости
Свойства перпендикулярных прямой и плоскости
Перпендикулярность плоскостей
Признак перпендикулярности плоскостей
Свойство перпендикулярных плоскостей
Ответы к устному опросу по теме “Перпендикулярность прямых и плоскостей”
Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости. Расстояние от точки до плоскости
Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости
Свойства перпендикуляра к плоскости
🔍 Видео

Видео:10 класс, 18 урок, Теорема о прямой, перпендикулярной к плоскостиСкачать

Перпендикулярные прямые

Две прямые в пространстве называются перпендикулярными , если угол между ними составляет .

При этом прямые могут пересекаться,

а могут быть скрещивающимися:

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Перпендикулярность прямой и плоскости

Прямая называется перпендикулярной к плоскости , если она перпендикулярна любой прямой, лежащей в этой плоскости.

Признак перпендикулярности прямой и плоскости

Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Свойства перпендикулярных прямой и плоскости

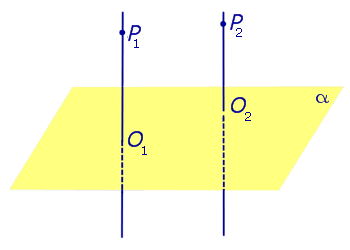
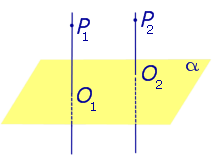
1). Две прямые, перпендикулярные одной и той же плоскости, параллельны.

2). Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.

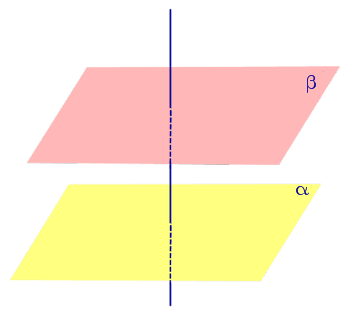
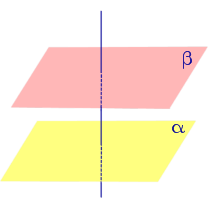
3). Две плоскости, перпендикулярные одной и той же прямой, параллельны между собой

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Перпендикулярность плоскостей

Пересекающиеся плоскости называются перпендикулярными , если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Признак перпендикулярности плоскостей

Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Свойство перпендикулярных плоскостей

Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна второй плоскости.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:№118. Точки А, М и О лежат на прямой, перпендикулярной к плоскости α, а точки О, В, С и D лежатСкачать

Ответы к устному опросу по теме “Перпендикулярность прямых и плоскостей”

Две прямые называются перпендикулярными, если угол между ними равен 90o. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в плоскости. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости. Верно ли утверждение: если две прямые в пространстве перпендикулярны к третьей прямой, то эти прямые параллельны? ( Нет не верно. Две прямые перпендикулярные третьей могут быть скрещивающимися. Или если они лежат в одной плоскости, а третья не принадлежит этой плоскости.) Прямая а перпендикулярна к плоскости α, а прямая в не перпендикулярна к этой плоскости. Могут ли прямые а и в быть параллельными? (Нет. Если a||b, то, поскольку а⊥б то и b⊥б, но по условию b не перпендикулярна б.) Параллельные прямые в и с лежат в плоскости α, а прямая а перпендикулярна к прямой в. Верно ли утверждение: а) а перпендикулярна к с; б) а пересекает α?

Прямая а параллельна плоскости α, а прямая в перпендикулярна к этой плоскости. Верно ли утверждение, что а и в взаимно перпендикулярны?( Да. Пусть K — точка пересечения b и б. Параллельно перенесем прямую а так, чтобы она прошла на пл. б через т. K: K ∈ a’, a’ || a. Раз b ⊥ б, то b ⊥ a’. Отсюда заключаем, что b ⊥ a.)

Сколько перпендикуляров можно провести через данную точку к данной прямой на плоскости?(Один)

Решение теста по теме “Перпендикулярность прямых и плоскостей”

Угол между двумя прямыми равен 90?. Как называются эти прямые?

Вам необходимо выбрать один вариант ответа, который Вы считаете правильным.

Одна из скрещивающихся прямых перпендикулярна плоскости, а вторая не пересекает эту плоскость. Могут ли быть параллельны эти прямые?

Расположите в правильной последовательности.

А) перпендикулярной к плоскости если;

Б) лежащей в данной плоскости;

В) прямая называется;

Г) она перпендикулярна к любой прямой.

Ответ: 1) В; 2) А; 3)Г; 4)Б.

Соотнесите написанное в столбцах 1 и 2.

А) Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то…

1) и другая прямая перпендикулярна к этой плоскости

Б) Если одна из двух параллельных прямых перпендикулярна к плоскости, то…

2) и другая прямая перпендикулярна к этой прямой.

В) Если две прямые перпендикулярны к плоскости, то…

3) они параллельны.

Ответ: А)-2 ; Б) -1; В) -3.

Выберите правильный ответ.

Сколько перпендикуляров можно провести через данную точку к данной прямой на плоскости?

Г) бесконечное множество.

Используя символы || и ⊥ запишите, как расположены прямая и плоскость.

СС1 и DCB D1C1 и DCB АА1 и DCB В1С1 и DCB

Ответ: 1) СС1 ⊥ (DCB); 2) D1С1 || (DCB); 3) AA1 ⊥ (DCB); 4) B1C1 || (DCD).

Сформулируйте признак перпендикулярности прямой и плоскости.

Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

ABCD — квадрат. АЕ — перпендикулярно плоскости квадрата, К ∈ BE. Чему равен угол между ВС и АК? Найти: ∠ (ВС; АК).

1) Так как ВС и АК — скрещивающиеся прямые, то ∠(ВС, АК) = ∠(АК; AD), т. к. ВС || AD (по свойству сторон квадрата).

2) AE ⊥ AD (по определению прямой, перпендикулярной плоскости), АВ ⊥ AD, т. к. ∠BAD = 90°, АЕ ∩ АВ = А, значит, AD ⊥ (АВЕ) (по признаку перпендикулярности прямой и плоскости).

3) Так как AD ⊥ (АВЕ), то AD ⊥ АК, АК ⊂ (АВЕ) (по определению прямой, перпендикулярной плоскости). Значит, ∠ (АК, АВ) = ∠KAD = 90°.

Диагональ BD параллелограмма ABCD перпендикулярна плоскости б. Найдите периметр параллелограмма, если АВ = 7 см, точки А и С лежат в плоскости б.

1) Так как А ∈ б, С ∈ б, то AC⊂б и BD⊥б (по определению прямой, перпендикулярной плоскости). Значит, ABCD — ромб (по признаку). Тогда АВ = ВС = CD = AD = 7 см (по определению ромба).

2) РABCD = 4 · 7 = 28 (см).

Решение контрольной работы по теме “Перпендикулярность прямых и плоскостей”

1. Длина стороны ромба ABCD равна 5 см, длина диагонали BD равна 6 см. Через точку О пересечения диагоналей ромба проведена прямая ОК, перпендикулярная его плоскости. Найдите расстояние от точки К до вершин ромба, если ОК = 8 см.

Дано: ABCD — ромб. АВ = 5 см. BD = 6 см. OK ⊥ (ABC), OK = 8 см.

Найти: КА, КВ, КС, KD.

KO⊥ (ABC) => KO⊥ AC, KO⊥ BD. AC ∩ BD=O =>BO=OD, AO=OC — свойство диагоналей ромба. KB1, KC1, KA1, KD — наклонные к плоскости (ABCD) из одной точки. КА = КС, КВ = KD.

Из ДКОВ: ∠O = 90°; КО = 8 см, ВО = OD = 3 см. По теореме Пифагора

KB = ; KB= = ; KB = KD= .

Из ДВОА: ∠O = 90°; ОВ = 3 см, АВ = 5 см. По теореме Пифагора

= — ; =

Из ДКОА: ∠O = 90°. По теореме Пифагора

= + ; =; AK = = 4 см.

Ответ: KB = KD= ; AK = = 4 см.

2. Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна 2√6 см, а его измерения относятся как 1:1:2. Найдите: а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания.

Дано: АС1 — прямоугольный параллелепипед. ABCD — квадрат, B1D = 2√6 см; AD : DC :DD1 = 1 : 1 : 2. (рис. 7).

Найти: a) AD, DC, DD1; б) sin ∠BDB1.

а) По теореме о свойстве диагонали параллелепипеда имеем: Пусть AD = х см, тогда

(Ответ: )

Видео:10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Прямая, перпендикулярная к плоскости.
Признак перпендикулярности прямой и плоскости.
Расстояние от точки до плоскости

Может ли прямая перпендикулярная к плоскости быть параллельна прямой лежащей в этой плоскости да нет

Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости

Свойства перпендикуляра к плоскости. Расстояние от точки до плоскости

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости

Определение . Прямой, перпендикулярной к плоскости , называют такую прямую, которая перпендикулярна к каждой прямой, лежащей на этой плоскости.

Признак перпендикулярности прямой и плоскости . Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в некоторой плоскости, то прямая перпендикулярна к этой плоскости.

Доказательство . Рассмотрим сначала следующий случай.

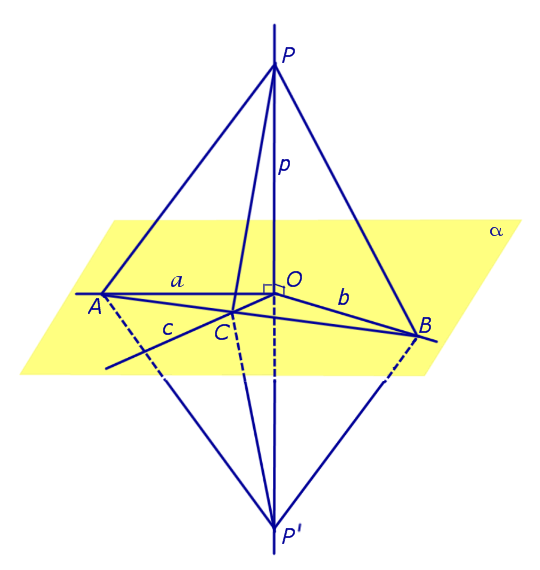
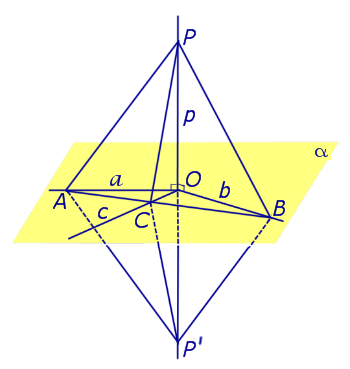
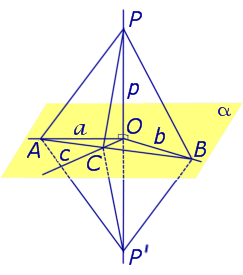
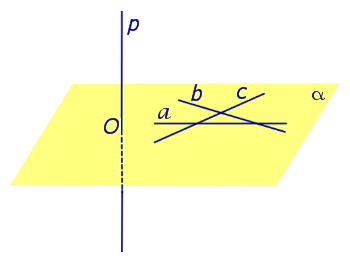
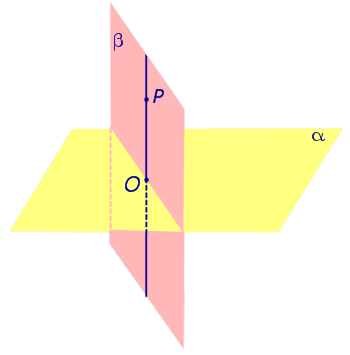
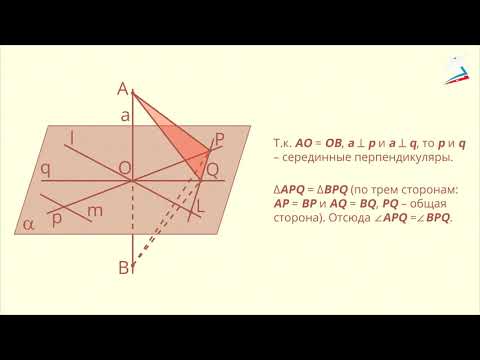
Предположим, что прямая p , пересекающая плоскость α в точке O, перпендикулярна к прямым a и b , лежащим на плоскости α и проходящим через точку O . Докажем, что в этом случае прямая p перпендикулярна любой другой прямой c , лежащей на плоскости α и проходящей через точку O .

С этой целью отметим на прямой a произвольную точку A , а на прямой b произвольную точку B (рис. 1).

Проведем прямую AB и обозначим буквой C точку пересечения прямых AB и c. Отметим на прямой p произвольную точку P и обозначим символом P’ точку, расположенную на прямой p так, чтобы точка O оказалась серединой отрезка PP’ . Поскольку прямые OA и OB являются серединными перпендикулярами к отрезку PP’ , то справедливы равенства

Из этих равенств, а также поскольку отрезок AB является общей стороной треугольников APB и AP’B , заключаем, что в силу признака равенства треугольников по трем сторонам трегольники APB и AP’B равны. Следовательно,

Отсюда в силу признака равенства треугольников по двум сторонам и углу между ними заключаем, что трегольник PBС равен треугольнику P’BС ( BP = BP’ , 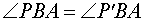, сторона BС — общая). Следовательно,

Таким образом, прямые PO и c перпендикулярны, что и требовалось доказать в рассматриваемом случае.

Теперь перейдем к общему случаю.

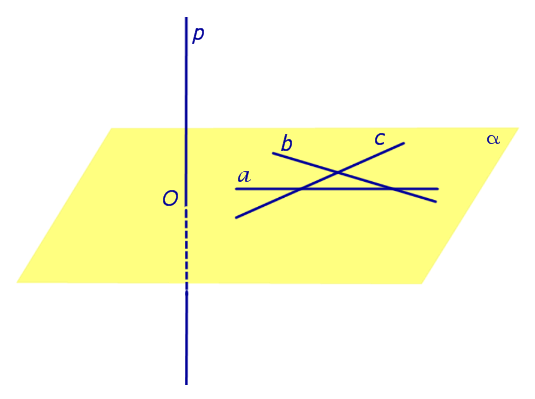
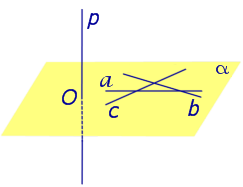
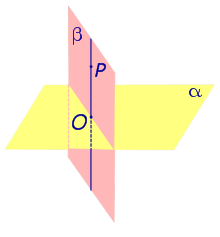
Предположим, что что прямая p , пересекающая плоскость α в точке O, перпендикулярна к прямым a и b , лежащим на плоскости α . Докажем, что в этом случае прямая p перпендикулярна любой другой прямой c , лежащей плоскости α (рис. 2).

С этой целью проведем через точку O прямые a’ , b’ и c’ соответственно параллельные прямым параллельные прямым a , b и c .

По определению угла между скрещивающимися прямыми прямая будет перпендикулярна прямым a’ и b’ , проходящим через точку O, и мы оказываемся в условиях уже рассмотренного случая.

Доказательство признака перпендикулярности прямой и плоскости завершено.

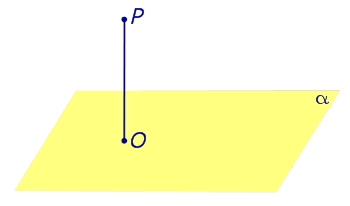
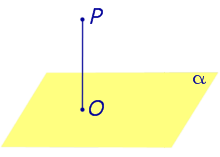
Замечание . Прямую, перпендикулярную к плоскости, часто называют перпендикуляром к плоскости. Точку перечения прямой, перпендикулярной к плоскости, с самой плоскостью называют основанием перпендикуляра.

Так, например, на рисунке 1 точка O является основанием перпендикуляра, опущенного из точки P на плоскость α .

Видео:10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

Свойства перпендикуляра к плоскости

Перечислим следующие свойства перпендикуляра к плоскости, доказательства которых мы оставляем читателю в качестве полезных упражнений.

Рисунок	Свойство
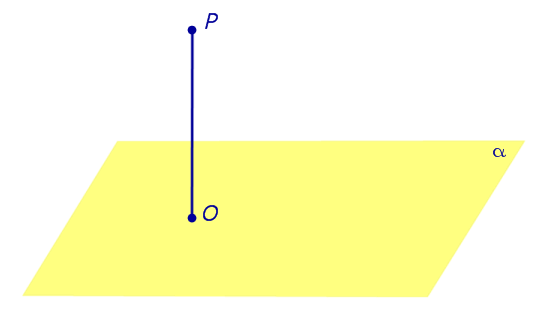	Из любой точки можно опустить перпендикуляр на любую плоскость. Если точка O — основание перпендикуляра, опущенного из точки P на плоскость α , то длину отрезка PO называют расстоянием от точки P до плоскости α.
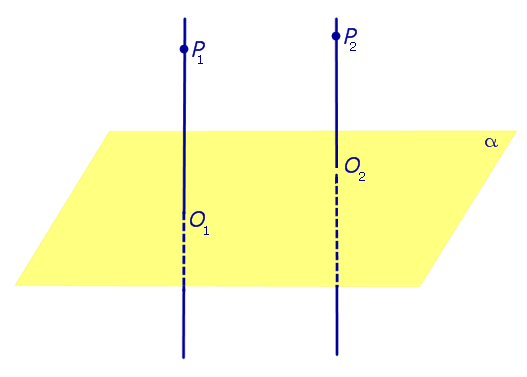	Два любых перпендикуляра к плоскости параллельны
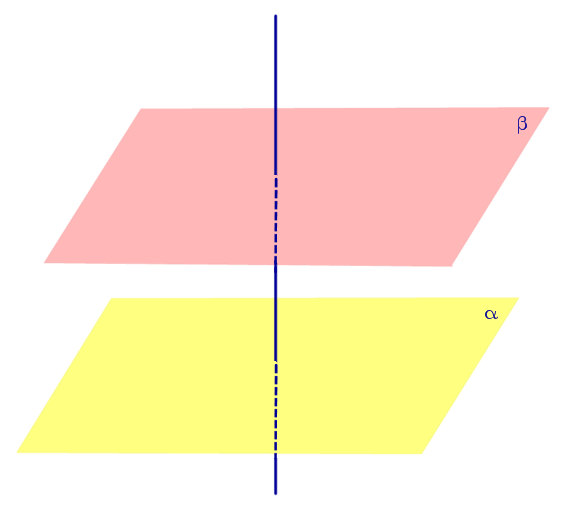	Плоскости, перпендикулярные к одной прямой, параллельны.
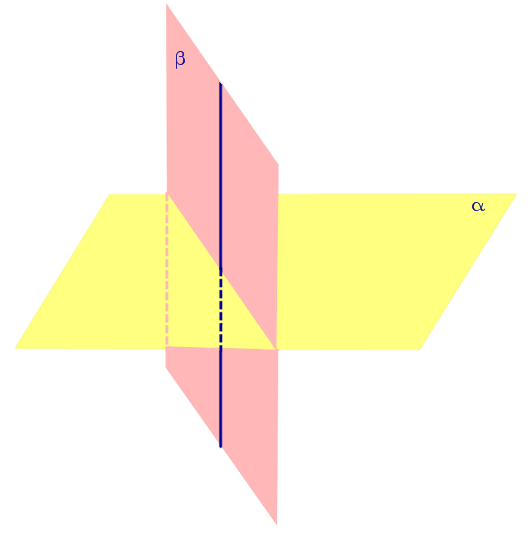	Если одна из плоскостей проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны.
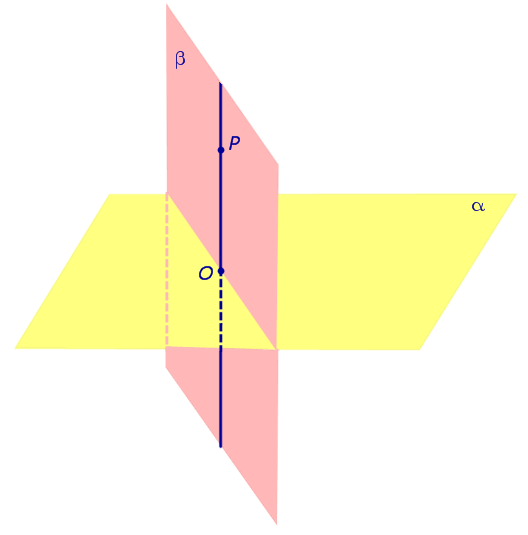	Если плоскости α и β перпендикулярны, а точка P лежит на плоскости β, то и перпендикуляр PO, опущенный из точки P на плоскость α , также лежит в плоскости β.

Свойство:
Из любой точки можно опустить перпендикуляр на любую плоскость. Если точка O — основание перпендикуляра, опущенного из точки P на плоскость α , то длину отрезка PO называют расстоянием от точки P до плоскости α.

Свойство:
Два любых перпендикуляра к плоскости параллельны параллельны

Свойство:
Плоскости, перпендикулярные к одной прямой, параллельны.

Свойство:
Если одна из плоскостей проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны.

Свойство:
Если плоскости α и β перпендикулярны, а точка P лежит на плоскости β, то и перпендикуляр PO, опущенный из точки P на плоскость α , также лежит в плоскости β.