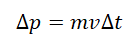Пример решения задачи по определению импульса сил, действующих, за определенное время, на материальную точку заданной массы, движущуюся по окружности с постоянной скоростью.
- Задача
- Импульс тела, закон сохранения импульса
- теория по физике 🧲 законы сохранения
- Относительный импульс
- Изменение импульса тела
- Частные случаи определения изменения импульса тела
- Абсолютно неупругий удар
- Абсолютно упругий удар
- Пуля пробила стенку
- Радиус-вектор тела повернул на 180 градусов
- Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
- Второй закон Ньютона в импульсном виде
- Реактивное движение
- Суммарный импульс системы тел
- Закон сохранения импульса
- Закон сохранения импульса в проекции на горизонтальную ось
- Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
- Сохранение проекции импульса
- § 2.7. Момент импульса
- 🎥 Видео
Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Задача
Материальная точка массой m=10 г движется по окружности с постоянной скоростью 40 см/с.
Найти импульс сил, действующих на точку за время прохождения точкой половины окружности (рисунок 2.3).
Видео:Физика - импульс и закон сохранения импульсаСкачать

Импульс тела, закон сохранения импульса
теория по физике 🧲 законы сохранения
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Видео:Физика - движение по окружностиСкачать

Относительный импульс
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p 1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
Видео:Урок 104. Импульс. Закон сохранения импульсаСкачать

Изменение импульса тела
∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар
Конечный импульс тела:
Модуль изменения импульса тела равен модулю его начального импульса:
Абсолютно упругий удар
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Пуля пробила стенку
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:
Радиус-вектор тела повернул на 180 градусов
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Угол падения равен углу отражения:
Модуль изменения импульса в этом случае определяется формулой:
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Видео:Импульс тела. Закон сохранения импульса | Физика 9 класс #20 | ИнфоурокСкачать

Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Видео:Урок 107. Задачи на закон сохранения импульса (ч.1)Скачать

Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:
Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:
Так как угол α = 90 о , вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Видео:Импульс тела и импульс силы. Закон сохранения импульса. 10 класс.Скачать

§ 2.7. Момент импульса
1. Пусть материальная точка массой т движется по окружности радиусом г со скоростью v (рис. 2.5), ее импульс р = т [см. (2.3)]. Моментом импульса L материальной точки относительно центра О называют произведение модуля ее импульса на радиус окружности:
Момент импульса L — это вектор, перпендикулярный плоскости, в которой лежат импульс р и радиус-вектор г (см. рис. 2.5).
2. Пусть на материальную точку массой т действует сила F, составляющая угол а с радиусом окружности г (рис. 2.6). Разложим эту силу на две составляющие: нормальную F„ = F cos а и тангенциальную FX = F sin а. Нормальная составляющая силы сообщает материальной точке нормальное (центростремительное) ускорение, вызывая поворот тела, но не меняя модуля скорости; тангенциальная составляющая сообщает материальной точке тангенциальное ускорение, т. е. меняет модуль скорости, не меняя ее направления. Итак, согласно второму закону Ньютона (2.13),
3. Пусть модуль момента импульса L [см. (2.24)] изменяется в течение промежутка времени At; при этом следует учесть, что здесь радиус и масса — величины постоянные. Тогда можно записать:
представляющее собой произведение силы F на плечо d (см. рис. 2.6), называют моментом силы. Из (2.25) и (2.26) получим
изменение момента импульса за единицу времени равно моменту силы.
Этот результат аналогичен выражению (2.12), согласно которому изменение импульса за единицу времени равно силе. Поэтому выражение (2.27) называют иногда вторым законом Ньютона для вращательного движения.
4. Если суммарный момент сил, действующих на систему, равен нулю, то изменение вектора момента импульса за единицу времени, согласно (2.27), тоже равно нулю, а это означает, что момент импульса является постоянной величиной, т. е. не меняется ни по модулю, ни по направлению. Оказывается, что наряду с законом сохранения импульса (см. § 2.2) справедлив закон сохранения момента импульса, который формулируется так:
Суммарный момент импульса замкнутой системы в результате действия внутренних сил не меняется.
Закон сохранения момента импульса является столь же фундаментальным законом природы, как и закон сохранения импульса. Справедливость этих законов подтверждается всей совокупностью физических знаний.
Таким образом, если внешние силы не действуют на уже вращающееся тело, иными словами, момент сил М= 0, то AL = 0, т. е. вектор момента импульса L уже вращающегося тела не изменяется ни по модулю, ни по направлению.
Так, можно наблюдать вращающихся конькобежца или балерину. Это значит, что у них вектор момента импульса вдоль оси симметрии остается постоянным. При отсутствии трения их вращение продолжалось бы бесконечно долго.
На этом же принципе работает гироскоп. Гироскопом называют всякое тело вращения, которое вращается вокруг точки, лежащей на оси симметрии тела.
Гироскоп нашел широкое применение на практике. Например, гироскоп на спутнике сохраняет в космосе его положение относительно Солнца; гироскоп на корабле до некоторой степени успокаивает его качку; установив ось гироскопа в направлении север—юг, имеют так называемый гирокомпас. Используя гирокомпас, можно поддерживать заданное направление корабля («авторулевой») или самолета («автопилот»). Гироскопом является сам снаряд или пуля, вылетающие из винторезного ствола. В полете они сохраняют направление оси симметрии. В боевых морских торпедах устанавливают гироскоп для сохранения направления на цель после их пуска и т. д.
🎥 Видео
Урок 109. Момент импульса. Закон сохранения момента импульсаСкачать

Центростремительное ускорение. 9 класс.Скачать

Физика 10 класс (Урок№11 - Импульс. Закон сохранения импульса.)Скачать

Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Закон сохранения импульса. Реактивное движение | Физика 10 класс #17 | ИнфоурокСкачать

Импульс тела и импульс силы. Законы изменения и сохранения импульса | Физика ЕГЭ, ЦТСкачать

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Закон изменения импульсаСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Закон сохранения импульсаСкачать