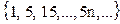Множества треугольников на плоскости

7, то x ∈ A, а если x не делится на 7, то, конечно, x не делится на 14 и поэтому x ∈ B. Итак, Vx ∈ Z обязательно выполнено хотя бы одно из включений x ∈ A, x ∈ B. Поэтому A U B = Z — множество всех целых чисел. Далее, чтобы найти пересечение A ∩ B, рассмотрим числа, которые одновременно и делятся на 7, и не делятся на 14. Это следующие числа: ±7, ±21, ±35. Поэтому

Пусть T — множество всех треугольников на плоскости. Рассмотрим его подмножества: Ti = , T2 = , T3 = . Найти множества Ti ∩ T2, Ti U T2, Ti ∩ T3, T2 Ti, T3 T2, T2 ∩ T3.

Решение. Найдём Ti∩T2. Так как любой равносторонний треугольник является также и равнобедренным, то T2 ⊆ Ti, и поэтому Ti ∩ T2 = T2. По этой же причине Ti U T2 = Ti. Пересечение Ti ∩ T3 состоит из прямоугольных равнобедренных треугольников (с углами 90°, 45°, 45°). Разность T2 Ti = ∅, так как T2 С Ti. Разность T3 T2 состоит из прямоугольных треугольников, которые не являются равносторонними. Однако все прямоугольные треугольники не являются равносторонними. Поэтому T3 T2 = T3 и T2 ∩ T3 = ∅.

С помощью диаграмм Эйлера-Венна проверить, что для любых множеств A, B справедливы соотношения (законы де Моргана): A ∩ B = A U B, A U B = A ∩ B.

Решение. Рассмотрим только первое равенство. Построим диаграмму Эйлера-Венна, изобразив множества A, B кругами. Считаем, что A, B есть подмножества некоторого универсального множества U, изображаемого прямоугольником.

Отметим штриховкой на диаграмме множество A ∩ B — дополнение к пересечению A и B:

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Треугольники, множества и алгебра

Иногда кажется, что некоторые математические темы изучены вдоль и поперек, например, треугольники. Ну что в этих треугольниках может быть нового и интересного? Тем не менее, даже такие, казалось бы, тривиальные объекты могут предстать под неожиданным углом. Давайте возьмем какую-нибудь простенькую задачку и попробуем ее решить. Постараемся найти треугольник с целочисленными сторонами, медианами и площадью. Мало ли, вдруг у нас получится.

Как перечислить все треугольники?

Даже несмотря на то, что некоторые множества содержат бесконечное количество элементов, они являются перечислимыми. Например, множество четных чисел может быть перечислено с помощью очень простого алгоритма — для любого n выдаем 2n и все. Во многом такая простота перечислимости некоторых множеств обусловлена тем, что элементы как-то упорядочены. Фактически, перечислить — значит пронумеровать, например, 2 — это первое четное число, 6 — третье. Но можем ли мы проделать то же самое с треугольниками? Если задавать треугольники с помощью кортежей вида a,b,c, то можем ли мы сказать, что треугольник 1,1,1 является первым, а треугольник 3,2,2 — четвертым или восьмым или еще каким-нибудь номером? Оказывается, можем.

Первое, что нужно придумать — это то как упорядочить множество треугольников. Первое, что приходит в голову — взять треугольник с какой-нибудь одной фиксированной стороной и выписать другие треугольники, стороны которого не меньше заданной. Например, так:

Как видим, первая сторона неизменна, а третья не превосходит суммы двух первых, на графике это будет выглядеть так:

Перед нами две ступенчатые функции, а значит мы можем задать стороны всех таких треугольников следующим образом:

Если заменить тройку на а на , то получим следующее:

Теперь любой треугольник можно изображать в виде точки на координатной плоскости, преобразуя стороны треугольников в координаты по двум простым формулам:

Чтобы перейти от координат к номерам достаточно воспользоваться канторовской нумерацией:

Или, если вместо координат использовать стороны треугольника:

Не знаю как вы, а я очень удивился, когда понял, что у каждого треугольника с целыми сторонами может быть свой номер. Есть что-то необычное в том, что подмножества треугольников, например, равнобедренные, могут выглядеть вот так:

Причем тут алгебра?

Очень похоже, что номера равнобедренных треугольников представляют собой множество парабол, нарисованных на одном графике. Так и есть, каждая из них может быть задана уравнением вида:

То же самое можно сказать и про многие другие подмножества треугольников. Например, вот так будут выглядеть треугольники с целыми, четными сторонами и одной целой медианой, проведенной к стороне :

На графике с координатами расположено множество кубических функций вида:

Не знаю, можно ли задать функции для всех кубических функций, но некоторые из них могут быть заданы, например, так:

Можно взять какую-то отдельную из них, например при j=0 и получить следующие формулы для координат треугольников:

Используя данные координаты можем задать функции для сторон и медианы:

Мы можем попробовать провернуть то же самое для треугольников, у которых две целые медианы:

Хоть этого и не видно на графике, но координаты треугольников с двумя целыми медианами задаются кубическими, квадратичными и линейными функциями. К сожалению, не могу привести все выкладки куда−то потерялись записи.

Если мы нарисуем график для треугольников с тремя целыми медианами, то получим следующее:

Таких треугольников очень мало, они очень сильно разрежены, но любопытно, что если найти хотя бы один такой треугольник, то все последующие могут быть заданы как:

Например, если взять треугольник 136, 170, 172 и умножить его стороны на 5, то мы снова получим треугольник с целыми сторонами и медианами.

Почему это все бесполезно?

Сначала кажется, что нумерация треугольников это шажок в сторону создания системы диофантовых уравнений, которые определяли бы стороны треугольников с целыми сторонами и медианами. Затем эти уравнения можно было бы подставить в формулу Герона и потом попытаться доказать возможность получения или неполучения треугольников с целой площадью. Но, к сожалению, нумерация треугольников абсолютно бесполезна в этом направлении. Все дело в том, что сама задача поиска треугольников с целыми сторонами и медианами связана с простыми числами. Сначала это кажется не совсем очевидным, но если следующее тождество является верным

то медиана не может быть целым числом. А это значит, что сама задача поиска треугольников с целыми сторонами и медианами наверняка может быть переведена на язык теории чисел, правда не знаю как.

В заключение

Сама идея того, что можно навести какой-никакой порядок в неупорядоченных множествах, очень любопытна. Например, можно попытаться каким-нибудь образом упорядочить матрицы из натуральных чисел, или графы определенного типа. Можно ли извлечь какую-то пользу от такого упорядочивания, это уже другой вопрос.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Счетные множества. Мощность континуума

Эквивалентные множества

1. Установить взаимно–однозначное соответствие между множеством всех натуральных чисел и множеством натуральных чисел, кратных 5.

2. Установить биекцию полуокружности и ее диаметра.

3. Установить биекцию двух окружностей; двух кругов.

4. Найти взаимно–однозначное отображение отрезка на отрезок (геометрически и аналитически).

Пусть , , тогда

.

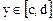
5. Найти взаимно–однозначное отображение интервала 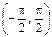на всю числовую прямую (геометрически и аналитически).

Пусть , , тогда .

6. (Отель Гилберта). Где-то в далеком космосе есть гостиница с бесконечным числом одноместных номеров, причем все они заселены. В гостиницу приехал человек и попросил поселить его в отдельный номер. Администратор сумел удовлетворить его просьбу, не выселив при этом ни одного постояльца. Как ему удалось это сделать?

Занумеруем номера числами 1, 2, 3, …, n , … Переселим постояльца из 1-го номера во 2-й, из 2-го в 3-й, …, из n-го – в (n+1)-й и т.д. Таким образом, мы освободим 1-й номер, в который и поселим нового постояльца.

7. Найти взаимно–однозначное отображение отрезка на полусегмент .

Так как на первом промежутке точек как бы на одну «больше», то нужно куда-то убрать «лишнюю» точку.

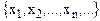
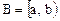
Возьмем на каждом из промежутков произвольную последовательность и поступим так же, как с отелем Гилберта: точке x₁ из множества поставим в соответствие точку x₂ из множества , точке x₂ из А –

точку x₃ из В, …, точке x_n из А – точку x_n+1 из В и т.д. Таким образом, в В освободится точка x₁, которую мы и поставим в соответствие точке b из множества А. Остальные точки в множествах А и В одинаковые, следовательно, мы их поставим в соответствие друг другу.

Таким образом, получим взаимно-однозначное соответствие между А и В.

8. Доказать, что все конечные промежутки числовой прямой эквивалентны.

Как уже показано в № 4, все одноименные промежутки (то есть все сегменты, все интервалы и т.д.) эквивалентны между собой, а в предыдущем примере мы показали, что и разноименные промежутки тоже эквивалентны, что и требовалось доказать.

9. Доказать, что любой промежуток числовой прямой эквивалентен всей числовой прямой.

10. Существует ли непрерывная функция, отображающая взаимно–однозначно отрезок на всю числовую прямую?

Нет, так как, если функция непрерывна на сегменте, то множеством ее значений тоже является сегмент.

Домашние примеры

11. Найти взаимно–однозначное отображение отрезка на интервал .

отображаем в (аналогично задаче 7, только в последовательность «прячем» две точки).

12. Найти взаимно–однозначное отображение полусегмента на луч .

С помощью функции y = tgx.

13. Существует ли непрерывная функция, отображающая взаимно–однозначно отрезок на интервал ?

14. Существует ли непрерывная функция, отображающая взаимно–однозначно отрезок на множество, состоящее из двух отрезков?

В 13 и 14 ответ «нет» (см. задачу 10).

15. Установить взаимно–однозначное соответствие между окружностью и прямой.

Точке О соответствует бесконечно удаленная точка числовой прямой.

Счетные множества. Мощность континуума

1. Какова мощность множества ?

Это множество является объединением двух последовательностей. Поскольку последовательность – это счетное множество, то и множество А счетно.

2. Какова мощность множества точек на плоскости, у которых обе координаты рациональны?.

Множество точек на плоскости с рациональными координатами можно представить в виде . Таким образом, это множество, элементы которого различаются двумя значками, пробегающими счетное множество значений, следовательно, по лемме 2.1 это множество счетно.

3. Какова мощность множества всех треугольников на плоскости, вершины которых имеют рациональные координаты?

Это множество счетно (см. задачу 2).

4. Доказать, что множество всех окружностей на плоскости, радиусы которых рациональны и координаты центра – рациональные числа, счетно.

5. Доказать, что если расстояние между любыми двумя точками множества Е на прямой больше 1, то множество Е не более, чем счетно.

Окружим каждую точку множества окрестностью, длиной 1, тогда эти окрестности не будут пересекаться. В каждой окрестности выберем рациональное число. Получим некоторое множество А рациональных чисел, которое находится во взаимно-однозначном соответствии с множеством Е. Так как множество А – часть множества Q, то оно не более чем счетно, следовательно, множество Е тоже не более чем счетно.

6. Доказать эквивалентность сегмента и интервала , пользуясь теоремами о свойствах бесконечных множеств.

Так как и множество несчетно, то по теореме 3.2 эквивалентен .

7. На прямой задано множество попарно не пересекающихся отрезков. Что можно сказать о мощности этого множества?

Это множество не более чем счетно (см. задачу 5).

8. Доказать, что множество точек разрыва монотонной функции, заданной на всей числовой прямой, конечно или счетно.

Во-первых, поскольку функция задана на всей числовой прямой, то она может иметь лишь точки разрыва 1-го рода, т.е. конечные скачки.

Поставим каждой точке разрыва, например, х₁ в соответствие сегмент 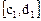, характеризующий величину скачка в этой точке. Очевидно, что для монотонной функции это соответствие будет взаимно-однозначным, и указанные сегменты не пересекаются. Тогда в силу задачи 7 их множество не более чем счетно, следовательно, не более чем счетно и множество точек разрыва.

🔍 Видео

Математика без Ху!ни. Уравнение плоскости.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Множество. Элементы множества. 5 класс.Скачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Построение следов плоскостиСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Математика это не ИсламСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Математика для всех. Алексей Савватеев. Лекция 2.7. Замощение плоскостиСкачать

Лекция 2. Особые линии плоскости. Линия ската плоскости.Скачать

Задача №2. На плоскости α(АВС) построить множества точек, равноудаленных от концов отрезка [DE].Скачать

Определение истинной величины двугранного угла АВСD при ребре АВ методом замены плоскостей проекцииСкачать

9 класс, 2 урок, Множества и операции над нимиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать