Задача: разбить произвольный многоугольник на треугольники.
- Клас, что-то наподобие списка, где можно двигаться вперед-назад и конец соединен с началом. То есть замкнутый круг, элементами которого будут объекты описаны пунктом ниже.
- Клас для представления точки. В нем, как полагается, должны быть координаты х и у. Так же еще одно поле в котором записано значение угла соответствующего этой точке в многоугольнике
- Функция, на вход которой идут два векторы, а на выход — угол между ними
- Функция, на вход которой идет точка и треугольник, на выход — признак, лежит ли точка внутри треугольника.
Теперь сам алгоритм.
Подготовка рабочих объективов.
Результатом работы должен быть список треугольников (result), потому создаем пустой список. Рабочий двунаправленный замкнутый список (points), представляющий многоугольник.
Перед стартом просчитываем углы для всех точек многоугольника.
Выбираем любую точку многоугольника как «рабочую» (p(i)).
- Создаем пустой список для хранения временных треугольников.
Если точка слева от «рабочий» (p(i)->left) имеет угол меньше чем 180 градусов и треугольник (p(i), p(i)->left, p(i)->left->left) не содержит внутри себя других точек многоугольника — заносим этот треугольник в наш временный список.
Если точка справа от «рабочий» (p(i)->right) имеет угол меньше чем 180 градусов и треугольник (p(i), p(i)->right, p(i)->right->right) не содержит внутри себя других точек многоугольника — заносим этот треугольник в наш временный список.
Если «рабочая» точка (p(i)) имеет угол меньше чем 180 градусов и треугольник ( p(i)->left, p(i),p(i)->right) не содержит внутри себя других точек многоугольника — заносим этот треугольник в наш временный список. - Если временный список не содержит треугольников — выбираем вместо «рабочий», точку слева от нее и возвращаемся к первому пункту.
Если содержит — выбираем треугольник с минимальной разницей между минимальным и максимальным углом (нужно пересчитать значение углов), заносим его в список result, удаляем из points среднюю точку из треугольника который выбрали а соседним точкам от нее (в points) пересчитываем значения углов, первую точку выбираем в качестве «рабочей» (p(i)).Если в points осталось только две точки — прекращаем работу, список треугольников содержится в res, иначе возвращаемся к первому пункту.
Теперь пара слов об оптимизации алгоритма.
На втором этапе выбирается треугольник с минимальной разницей между минимальным и максимальным углом для того, чтобы треугольник был максимально подобный к правильному, иногда это важно. Если же вам нет разницы как выглядит треугольник — тогда можно не создавать временный список треугольников, а выбрать первый из трех возможных треугольников который не содержит внутри себя другую точку многоугольника и угол, который образует средняя точка треугольника в многоугольнике меньше 180 градусов. Такое упрощение значительно снизит вычислительные затраты.
Еще, если уверены, что многоугольник выпуклый — тогда не нужно проверь содержит ли треугольник другие точки многоугольника.
П.С. Я не встречал такой алгоритм на просторах инета, хотя и уверен, что что-то подобное уже есть.
Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Урок по математике на тему «Разбиение многоугольника на треугольники», программа «Перспективная начальная школа»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику


Тема: «Разбиение многоугольника на треугольники» (1 урок)
Прозвенел уже звонок.
Куда мы с вами попадём –
Узнаете вы скоро.
В известном мультике найдём
— Ребята, кто пришёл к нам в гости? (Серый волк и лиса). А почему именно эти герои? (Потому что скоро Новый год). В Новый год бывают разные приключения. И вот однажды одни мальчик и девочка написали письмо Деду Морозу и попросили Снеговика Почтовика доставить это письмо Деду Морозу. Но как вы уже знаете, снеговику по пути встретились лиса и волк, которые хотели отобрать письмо. Как вы думаете, что произошло со Снеговиком? (Когда Снеговик убегал от них, он рассыпался на части). Ребята, Снеговик просит вас помочь ему в его беде. Волк и лиса отдадут вам части Снеговика только тогда, когда вы выполните их задания.
(На доске фрагменты Снеговика)
Итак, ребята, за правильно выполненное задание волк будет отдавать вам фрагменты снеговика.
Актуализация знаний. Повторение пройденного материала. (2 -3 мин.)
— Ребята, посмотрите на слайд, какую геометрическую фигуру вы видите? (Многоугольник)
— Как называются отрезки красного цвета? (Сторона многоугольника)
— Как называются отрезки зелёного цвета? (Диагональ)
— Чем сторона многоугольника отличается от его диагонали?
(Сторона соединяет две соседние вершины, а диагональ соединяет две вершины, не принадлежащие одной его стороне)
Постановка цели и задач урока. (2 мин.)
— Что делает диагональ с многоугольником? (Делит многоугольник на другие геометрические фигуры)
— В нашем случае, на какие геометрические фигуры разбит многоугольник? (На треугольники)
— Ребята, чему мы будем с вами сегодня учиться?
(Разбивать многоугольники на треугольники)
Первичное усвоение новых знаний . Работа с учебником .
( У учеников карточки с многоугольниками )
— Откройте учебник на стр. 108. Прочитайте задание №376
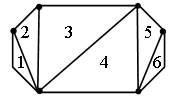
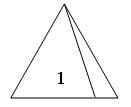
— В данном шестиугольнике проведи все возможные диагонали из одной его вершины. (Дети работают самостоятельно)
(Слайд 1). Один ученик разбивает шестиугольник на треугольник на слайде.
— Сколько треугольников получилось? (4 треугольника).
— Давайте построим шестиугольники и проведём в них всевозможные диагонали только из других вершин. (Дети выполняют построение шестиугольников и выполняют задание – у детей карточки с вершинами шестиугольников ).
На доске проецируются различные чертежи, зависящие от выбора вершин. Дети сверяют со своими чертежами. (Проверка в группах)
— Ребята, волк просит вас сделать вывод о проделанной вами работы.
Дети делают вывод о том, что диагонали, выходящие из одной вершины шестиугольника, какую бы из вершин мы не выбрали, разбивают его на четыре треугольника.
Учитель даёт ребятам первый фрагмент туловища Снеговика, дети прикладывают его к голове Снеговика.
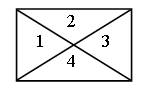
— Ребята, послушайте следующее задание волка — начертите в тетради прямоугольник и разбейте его на 4 треугольника (После самостоятельного выполнения, один ученик делит прямоугольник на слайде).
— Ребята, может быть у кого-нибудь из вас есть другие варианты?
— В каком случае прямоугольник разбит диагоналями, а в каких отрезками?
(1 вариант – диагоналями) – получают следующий фрагмент, прикрепляют к туловищу.
Следующее задание волка.
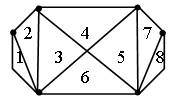
Разбей восьмиугольник на 8 треугольников.
— Ребята, кто знает, как это можно сделать?
Дети объясняют, как можно выполнить это задание.
Например, выбираем некоторую точку внутри восьмиугольника, а затем от этой точки проводим отрезки в каждую вершину восьмиугольника.
Дети выполняют чертёж в тетради, затем учитель проецирует чертёж на слайде. Дети сверяют свой чертёж с чертежом на слайде.
За выполненное задание дети получают следующий фрагмент снеговика.
Работа в тетради
— Ребята, давайте вспомним, какие треугольники вы знаете? (Остроугольный, тупоугольный и прямоугольный).
— Выберите из данных треугольников остроугольный. (Шаблоны на столах у ребят)
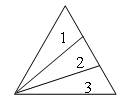
— начертите остроугольный треугольник и разбейте его на 3 треугольника. Один ученик выполняет задание на доске (шаблоны остр. треугольников на слайде)
Проверка чертежей. Дети сравнивают свои чертежи с чертежами на доске. (Получают фрагмент снеговика)
Выполнение задания №381. Работа с учебником
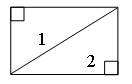
— Ребята, прочитайте задание в учебнике № 381, что нужно сделать? Возьмите прямоугольник и при помощи линейки и карандаша разбейте его на 2 прямоугольных треугольников.
— Ребята, что общего у получившихся треугольников?
У каждого есть прямой угол.
— Как называется линия в прямоугольнике, которую вы провели?
— Согните прямоугольник по диагонали. Какой вывод вы можете сделать?
Диагональ делит прямоугольник на 2 равных прямоугольных треугольников.
(Получают фрагмент Снеговика)
Выполнение задания № 382. (Карточка с различными многоугольниками)
Учитель просит самостоятельно прочитать задание.
Учащиеся самостоятельно читают задание и приступают к его выполнению.
На доске проверяют решение. (Работа в парах)
— Ребята, найдите площадь квадрата.
Дети выполняют решение на карточке. Проверяют вместе ответ. (Один ученик выполняет решение на доске)
Дети получают последний фрагмент снеговика.
— Молодцы ребята, у вас получилось собрать снеговика. И теперь он сможет передать письмо деду Морозу.
— Ребята, что вам понравилось на уроке? (ответ детей) А какие трудности у вас возникли? (ответ детей)
— Помогли ли задания волка вам научиться чертить многоугольники и разбивать их на треугольники? Если у вас всё получилось, то поднимите зелёный смайлик. Если у вас возникали затруднения, то жёлтый смайлик. (ответ детей)
— Что бы вы хотели пожелать волку в новом году?
Учитель задаёт домашнее задание (Т стр. 88 №157 – 158). Слайд 6
Вместе разбирают выполнение домашнего задания
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Конспект урока по математике на тему»Разбиение многоугольника на треугольники»4класс
Разбиение многоугольника
на треугольники
Цели: учить выполнять чертеж; формировать умение делить отрезками многоугольник на данное количество треугольников; закреплять умение определять количество сторон и количество диагоналей в многоугольнике.
1. Математический диктант.
а) Как называется результат сложения двух чисел?
б) Как называются числа, которые складывают?
в) Чему равна сумма 3456 + 0?
г) Запишите равенство 245 – 181 = 63. С помощью сложения проверьте, правильно ли выполнено вычитание.
д) Найдите значение выражения 981 – х, если х = 0.
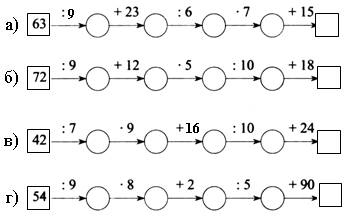
2. Какое число нужно вписать в последнюю клетку цепочки?
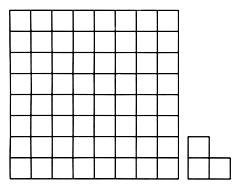
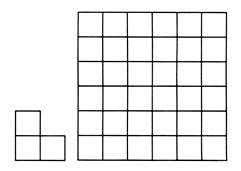
3. Как-то раз Пятачок зашёл в гости к Винни-Пуху. Тот в глубокой задумчивости смотрел на лист бумаги, где были нарисованы квадрат и уголок.
Винни-Пух объяснил, что хочет разрезать квадрат на уголки.
Пятачок внимательно посмотрел на эти фигуры и сказал, что такой квадрат разрезать на такие уголки нельзя. Почему? А вот такой квадрат можно разрезать на уголки. Покажите, как это сделать.
II. Работа по учебнику.
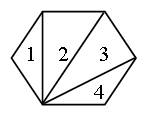
Задание 376. Начертите шестиугольник и проведите все возможные диагонали из одной его вершины.
– На какие фигуры эти диагонали разбивают шестиугольник? (На треугольники.) Сколько треугольников получилось? (4 треугольника.)
Задание 377. Начертите прямоугольник и разбейте его на 4 треугольника.
Задание 378. Как называется данный многоугольник? (Восьмиугольник.) Разбейте этот восьмиугольник на 6 треугольников.
– Разбейте этот же восьмиугольник на 8 треугольников.
Задание 379. Начертите остроугольный треугольник и разбейте его на 3 треугольника.
Задание 380. Начертите остроугольный треугольник и разбейте его на 2 треугольника так, чтобы один из них был остроугольным, а другой – тупоугольным.
1-й треугольник – остроугольный;
2-й треугольник – тупоугольный.
Задание 381. Разбейте прямоугольник на два прямоугольных треугольника. Используя модель прямоугольника, сделанную из бумаги, убедитесь, что полученные прямоугольные треугольники равны.
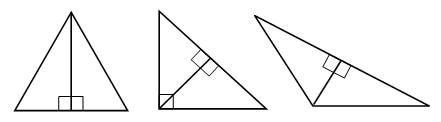
Задание 382. Начертите остроугольный, прямоугольный и тупоугольный треугольники. Разбейте каждый из них на два прямоугольных треугольника.
– Как называется отрезок, с помощью которого такое разбиение можно выполнить? (Высота треугольника.)
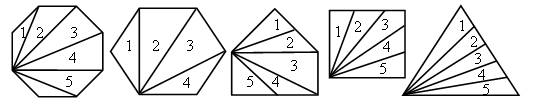
Задание 383. Как называются данные многоугольники? (Семиугольник, шестиугольник, пятиугольник, четырехугольник, треугольник.)
– Каждый многоугольник разбейте на 5 треугольников.
– Как можно разбить многоугольник на треугольники?
💡 Видео
Многоугольники. Математика 8 класс | TutorOnlineСкачать

Построение пятиугольника циркулемСкачать

Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Математика 5 Треугольники МногоугольникиСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Урок 6. Треугольники, четырёхугольники, многоугольники. ОГЭ. Вебинар | МатематикаСкачать

Выпуклые и невыпуклые многоугольникиСкачать
Площадь треугольника. Как найти площадь треугольника?Скачать

5 класс. МногоугольникиСкачать

9 класс, 21 урок, Правильный многоугольникСкачать

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИСкачать

Математика 5 класс (Урок№28 - Треугольники.)Скачать

9 класс. Геометрия. Правильные многоугольники и их свойства. Правильный треугольник. Урок #4Скачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

МногоугольникСкачать

Диагональ многоугольникаСкачать