Если две окружности имеют только одну общую точку, то говорят, что они касаются.
Если же две окружности имеют две общие точки, то говорят, что они пересекаются.
Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.
Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO1).
Теорема.
Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.
Пусть окружности O и O1 имеют общую точку A, лежащую вне линии центров OO1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO1.
Опустим из A на прямую OO1 перпендикуляр AB и продолжим его на расстояние BA1, равное AB. Докажем теперь, что точка A1 принадлежит обеим окружностям. Из построения видно, что точки O и O1 лежат на перпендикуляре, проведенном к отрезку AA1 через его середину. Из этого следует, что точка O одинаково удалена от A и A1. То же можно сказать и о точке O1. Значит обе окружности, при продолжении их, пройдут через A1.Таким образом, окружности имеют две общие точки : A (по условию) и A1 (по доказанному). Следовательно, они пересекаются.
Следствие.
Общая хорда (AA1) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.
Теоремы.
1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.
2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.
Признаки различных случаев относительного положения окружностей.
Пусть имеем две окружности с центрами O и O1, радиусами R и R1 и расстоянием между центрами d.
Эти окружности могут находиться в следующих 5-ти относительных положениях:
1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R1 .
2. Окружности имеют внешнее касание. Тогда d = R + R1, так как точка касания лежит на линии центров O O1.
3. Окружности пересекаются. Тогда d R + R1, потому что в треугольнике OAO1 сторона OO1 меньше суммы, но больше разности двух других сторон.
4. Окружности имеют внутреннее касание. В этом случае в d = R — R1, потому что точка касания лежит на продолжении линии OO1.
5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,
d R + R1, то окружности расположены одна вне другой, не касаясь.
2. Если d = R + R1, то окружности касаются извне.
3. Если d R — R1, то окружности пересекаются.
4. Если d = R — R1, то окружности касаются изнутри.
5. Если d R Е R1. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.
- Две окружности пересекающиеся под прямым углом
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- 🌟 Видео
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Две окружности пересекающиеся под прямым углом
Окружность – это фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки.
Основные понятия:
Центр окружности – это точка, равноудаленная от точек окружности.
Радиус – это расстояние от точек окружности до ее центра (равен половине диаметра, рис.1).
Диаметр – это хорда, проходящая через центр окружности (рис.1).
Хорда – это отрезок, соединяющий две точки окружности (рис.1).
Касательная – это прямая, имеющая только одну общую точку с окружностью. Проходит через точку окружности перпендикулярно диаметру, проведенному в эту точку (рис.1).
Секущая – это прямая, проходящая через две различные точки окружности (рис.1).
Единичная окружность – это окружность, радиус которой равен единице.
Дуга окружности – это часть окружности, разделенная двумя несовпадающими точками окружности.
1 радиан – это угол, образуемый дугой окружности, равной длине радиуса (рис.4).
1 радиан = 180˚ : π ≈ 57,3˚
Центральный угол – это угол с вершиной в центре окружности. Равен градусной мере дуги, на которую опирается (рис.2).
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Равен половине градусной меры дуги, на которую опирается (рис.3).
Две окружности, пересекающиеся под прямым углом, называются ортогональными.
Длина окружности и площадь круга:
Обозначения:
Длина окружности – C
Длина диаметра – d
Длина радиуса – r
Значение π:
Отношение длины окружности к длине ее диаметра обозначается греческой буквой π (пи).
Формула длины окружности:
C = πd, или C = 2πr
Формулы площади круга:
Площадь кругового сектора и кругового сегмента.
Круговой сектор – это часть круга, лежащая внутри соответствующего центрального угла.
Формула площади кругового сектора:
πR 2
S = ——— α
360
где π – постоянная величина, равная 3,1416; R – радиус круга; α – градусная мера соответствующего центрального угла.
Круговой сегмент – это общая часть круга и полуплоскости.
Формула площади кругового сегмента:
πR 2
S = ——— α ± SΔ
360
где α – градусная мера центрального угла, который содержит дугу этого кругового сегмента; SΔ — площадь треугольника с вершинами в центре круга и в концах радиусов, ограничивающих соответствующий сектор.
Знак «минус» надо брать, когда α 180˚.
Уравнение окружности в декартовых координатах x, y c центром в точке (a;b):
Окружность, описанная около треугольника (рис.4).
Если от середины каждой из сторон треугольника провести перпендикуляры, то точка их пересечения будет центром окружности, описанной около этого треугольника.
Окружность, вписанная в треугольник (рис.5).
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис этого треугольника.
Углы, вписанные в окружность (рис.3).
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность.
Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Основные понятия:
Угол делит плоскость на две части. Каждая из этих частей называется плоским углом.
Плоские углы с общими сторонами называются дополнительными.
Плоский угол с вершиной в центре окружности называется центральным углом (рис.2)
Пропорциональность отрезков хорд и секущих окружности.
Если хорды AB и CD окружности пересекаются в точке S, то
Если из точки P к окружности проведены две секущие, пересекающие окружность соответственно в точках A, B и C, D, то
Частные случаи и формулы:
1) Из точки C, находящейся вне окружности, проведем касательную к окружности и обозначим точку их соприкосновения буквой D.
Затем из той же точки C проведем секущую и точки пересечения секущей и окружности обозначим буквами А и B (рис.8).
CD 2 = AC · BC
2) Проведем в окружности диаметр AB. Затем из точки C, находящейся на окружности, проведем перпендикуляр к этому диаметру и обозначим получившийся отрезок CD (рис.9).
CD 2 = AD · BD.
Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
Видео:Две окружности на плоскости. Математика. 6 класс.Скачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | ||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||||
| Радиус |  | |||||||||||||||||||||||||||
| Хорда |  | |||||||||||||||||||||||||||
| Диаметр |  | |||||||||||||||||||||||||||
| Касательная |  | |||||||||||||||||||||||||||
| Секущая |  | |||||||||||||||||||||||||||
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:ОГЭ Задание 25 Две окружностиСкачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:Чему равна сторона треугольника, у которого медианы пересекаются под прямым угломСкачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема | ||||||||||||||||
| Пересекающиеся хорды |  | |||||||||||||||||
| Касательные, проведённые к окружности из одной точки |  | |||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки |  | |||||||||||||||||
| Секущие, проведённые из одной точки вне круга |  | |||||||||||||||||
| Пересекающиеся хорды | ||
 | ||
| Касательные, проведённые к окружности из одной точки | ||
 | ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
 | ||
| Секущие, проведённые из одной точки вне круга | ||
 | ||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:ТОП-3 конструкции с окружностями для №16 из ЕГЭ 2023 по математикеСкачать

Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:Плоскость. Пересекающиеся прямые. 6 класс.Скачать

Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
🌟 Видео
Диагонали ромба пересекаются под прямым угломСкачать

Две окружности соприкасаются внешним образом. к ним...Задача.Скачать

Две окружности пересекаются, если радиус одной ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Теорема о числе точек пересечения двух окружностейСкачать

Перпендикулярные прямые. 6 класс.Скачать

ЕГЭ Задание 16 Две окружностиСкачать

Геометрия Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второйСкачать

Две медианы треугольника пересекаются по прямым углом.Скачать

Две окружности/ Повторяем углыСкачать

Две окружности #shortsСкачать
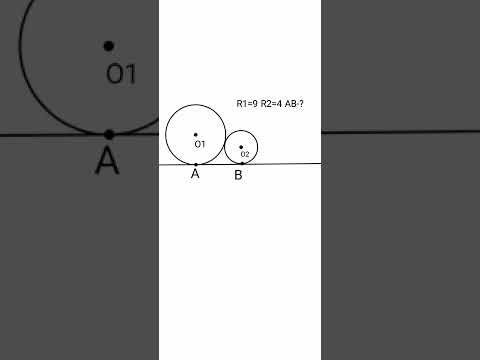
Задание 26 Две окружности, внешнее касаниеСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать