Прямая проведенная через вершину равнобедренного треугольника параллельно его основанию

Геометрия | 5 — 9 классы

Прямая проведенная через вершину равнобедренного треугольника параллельно его основанию является биссектрисой внешнего угла треугольника при той же вершине.

Внешний угол треугольника равен сумме двух внутренних,

не смежных с ним то есть сумме двух углов при основании

биссектриса делит внешний угол пополам значит половина внешнего угла равна углу при основании

теперь рассмотри основание, биссектрису как прямые и боковую сторону как секущую

противолежащие углы равны(внешние накрест лежащие)то прямые параллельны

значит биссектриса и основание — параллельные прямые.

Видео:№241. Прямая, параллельная основанию равнобедренного треугольника ABC, пересекает боковые стороны АВСкачать

Докажите, что основание равнобедренного треугольника параллельно биссектрисе одного из внешних углов?

Докажите, что основание равнобедренного треугольника параллельно биссектрисе одного из внешних углов.

Видео:№155. Через вершину прямого угла С равнобедренного прямоугольного треугольника ABCСкачать

Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника, противолежащей основанию, параллельна основанию?

Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника, противолежащей основанию, параллельна основанию.

Видео:№243. Через вершину С треугольника ABC проведена прямая, параллельная его биссектрисе АА1Скачать

Доказать, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна его основанию?

Доказать, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна его основанию.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Докажите, что если биссектриса внешнего угла треугольника параллельна стороне треугольника, то треугольник является равнобедренным?

Докажите, что если биссектриса внешнего угла треугольника параллельна стороне треугольника, то треугольник является равнобедренным.

Видео:№233. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника,Скачать

Докажите , что если биссектриса внешнего угла треугольника параллельна его стороне , то этот треугольник равнобедренный?

Докажите , что если биссектриса внешнего угла треугольника параллельна его стороне , то этот треугольник равнобедренный.

Видео:№420. Докажите, что прямая, содержащая биссектрису равнобедренного треугольникаСкачать

СРОЧНО НАДО?

Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника, противолежащей основанию, параллельна основанию.

Видео:№149. Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно,Скачать

Докажите, что биссектриса внешнего угла при вершине , противоположной основанию равнобедренного треугольника, параллельна ему?

Докажите, что биссектриса внешнего угла при вершине , противоположной основанию равнобедренного треугольника, параллельна ему.

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Внешний угол при вершине равнобедренного треугольника в 4 раза больше внутреннего при той же вершине?

Внешний угол при вершине равнобедренного треугольника в 4 раза больше внутреннего при той же вершине.

Скольким градусам равны внешние углы при основании этого треугольника?

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Помогите?

Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника, противолежащей основанию, параллельна основанию.

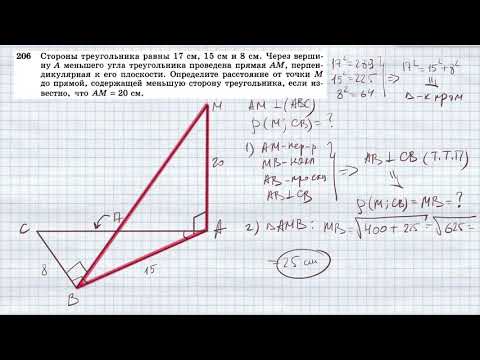
Видео:№206. Стороны треугольника равны 17 см, 15 см и 8 см. Через вершину A меньшего угла треугольника проСкачать

Помогите пожалуйстаДокажите, что у равнобедренного треугольника биссектрисы, проведенные из вершин при основании, равны?

Докажите, что у равнобедренного треугольника биссектрисы, проведенные из вершин при основании, равны.

На странице вопроса Прямая проведенная через вершину равнобедренного треугольника параллельно его основанию является биссектрисой внешнего угла треугольника при той же вершине? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

1)углы при основании равны т. К. треугольник р / б. (равнобедренный) 2)вершина = 180 — внешний угол = 180 — 130 = 50т. К. они смежные 3)любой угол при основании = (180 — 50) : 2 = 65т. К углы при основании равны и сумма углов треугольника = 180 О..

Вот весь ответ. Надеюсь, помогла.

Ответ 2) в ромб1 из углов равен 90 то квадр.

Сначала проводим касательную к окружности, затем хорду и радиус ОС. Схема и расчет — в приложении.

Ответ : 10 см Объяснение : Дано : АВСМ — трапеция, АВ⊥АМ, ВС = 8 см, ∠ВСМ = 150°. СН — высота. Найти СН. ΔСМН — прямоугольный, ∠МСН = 150 — 90 + 60°, ∠М = 90 — 60 = 30°значит, СН = 1 / 2 СМ как катет, лежащий против угла 30 градусовСН = 20 : 2 = 1..

Самое основное в этой задаче понять, почему треугольник BCD — равнобедренный. Вспомни накрест лежащие углы, они равны при параллельных прямых и секущей третьей. А треугольник является равнобедренным, если его углы при основании равны. Основанием т..

Длина СД = АВ * 5 = 4, 3 * 5 = 21, 5 см АВ + СД = 4, 3 + 21, 5 = 25, 8 см.

Ты не сказал шо делать с .

Участок, ограниченный эллипсом. Решение в приложении p. S. ждем продолжения.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Равнобедренный треугольник: свойства, признаки и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Геометрия Основание равнобедренного треугольника равно a а противолежащий ему угол равен α НайдитеСкачать

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Видео:Геометрия Высота равнобедренного треугольника, проведенная к основанию, равна h, а угол при вершинеСкачать

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Видео:35. Геометрия на ЕГЭ по математике. Трапеция.Скачать

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

Видео:№152. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. НайдитеСкачать

Прямая проведенная через вершину равнобедренного треугольника параллельно его основанию

Из этой теоремы следует, что в треугольнике против равных углов лежат равные стороны .

Если медиана треугольника является его биссектрисой, то этот треугольник равнобедренный.

Рассмотрим треугольник ABC , у которого отрезок BM — медиана и биссектриса. Надо доказать, что AB = BC .

На луче BM отложим отрезок MD , равный отрезку BM (рис. 171).

В треугольниках AMD и CMB имеем: AM = MC (так как по условию BM — медиана), BM = MD по построению, углы AMD и CMB равны как вертикальные. Следовательно, треугольники AMD и CMB равны по первому признаку равенства треугольников.

Тогда стороны AD и BC , углы ADM и CBM равны как соответственные элементы равных треугольников.

Так как BD — биссектриса угла ABC , то ∠ ABM = ∠ CBM . Поскольку ∠ CBM = ∠ ADM , то получаем, что ∠ ABM = ∠ ADM .

Тогда по теореме 10.3 получаем, что треугольник DAB — равнобедренный, откуда AD = AB . И уже доказано, что AD = BC . Следовательно, AB = BC .

Задача. В треугольнике ABC проведена биссектриса BM (рис. 172), ∠ BAK = 70°, ∠ AKC = 110°. Докажите, что BM ⊥ AK .

Решение. Так как углы BKA и AKC — смежные, то ∠ BKA = 180° — ∠ AKC . Тогда ∠ BKA = 180° — 110° = 70°.

Следовательно, в треугольнике ABK получаем, что ∠ BAK = ∠ BKA = 70°. Треугольник ABK — равнобедренный с основанием AK , и его биссектриса BO ( O — точка пересечения AK и BM ) является также высотой, т. е. BM ⊥ AK .

1. Сформулируйте признаки равнобедренного треугольника.
2. Какова связь между равными углами и равными сторонами треугольника?

232. В треугольнике ABC медиана BK перпендикулярна стороне AC . Найдите ∠ ABC , если ∠ ABK = 25°.

233. Серединный перпендикуляр стороны AC треугольника ABC проходит через вершину B . Найдите ∠ C , если ∠ A = 17°.

234. В треугольнике ABC известно, что ∠ ACB = 90°, ∠ A = ∠ B = 45°, CK — высота. Найдите сторону AB , если CK = 7 см.

235. На рисунке 173 ∠ AMK = ∠ ACB , AK = MK . Докажите, что ∆ ABC — равнобедренный.

236. Прямая, перпендикулярная биссектрисе угла A , пересекает его стороны в точках B и C . Докажите, что ∆ ABC — равнобедренный.

237. Биссектрисы AM и CK углов при основании AC равнобедренного треугольника ABC пересекаются в точке O . Докажите, что ∆ AOC — равнобедренный.

238. В треугольнике ABC биссектриса BK является его высотой. Найдите периметр треугольника ABC , если периметр треугольника ABK равен 16 см и BK = 5 см.

239. Верно ли утверждение:

1) если медиана и высота треугольника, проведённые из одной вершины, не совпадают, то этот треугольник не является равнобедренным;

2) если биссектриса треугольника делит противолежащую сторону пополам, то этот треугольник равнобедренный?

240. Медианы AE и CF , проведённые к боковым сторонам BC и AB равнобедренного треугольника ABC , пересекаются в точке M . Докажите, что треугольник AMC — равнобедренный.

241. Точки M и K принадлежат соответственно боковым сторонам AB и BC равнобедренного треугольника ABC , AM = CK . Отрезки AK и CM пересекаются в точке O . Докажите, что ∆ AOC — равнобедренный.

242. На сторонах AB и BC треугольника ABC отметили соответственно точки D и E так, что ∠ EAC = ∠ DCA . Отрезки AE и CD пересекаются в точке F , DF = EF . Докажите, что ∆ ABC — равнобедренный.

243. Через середину D стороны AB треугольника ABC проведены прямые, перпендикулярные биссектрисам углов ABC и BAC . Эти прямые пересекают стороны AC и BC в точках M и K соответственно. Докажите, что AM = BK .

244. Медиана AM треугольника ABC перпендикулярна его биссектрисе BK . Найдите сторону AB , если BC = 16 см.

245. Прямая, проходящая через вершину A треугольника ABC перпендикулярно его медиане BD , делит эту медиану пополам. Найдите отношение длин сторон AB и AC треугольника ABC .

246. В треугольнике ABC известно, что ∠ C = 90°, ∠ A = 67,5°, ∠ B = 22,5°, CK — биссектриса треугольника ABC , CM — биссектриса треугольника BCK (рис. 174). Докажите, что точка M — середина отрезка AB .

247. Длины сторон треугольника, выраженные в сантиметрах, равны трём идущим подряд натуральным числам. Найдите стороны этого треугольника, если одна из его медиан перпендикулярна одной из его биссектрис.

248. В треугольнике ABC известно, что AB = 3 см, BC = 4 см, AC = 6 см. На стороне BC отметили точку M такую, что CM = 1 см. Прямая, проходящая через точку M перпендикулярно биссектрисе угла ACB , пересекает отрезок AC в точке K , а прямая, проходящая через точку K перпендикулярно биссектрисе угла BAC , пересекает прямую AB в точке D . Найдите длину отрезка BD .

Упражнения для повторения

249. На прямой последовательно отметили точки A , B , C , D , E и F так, что AB = BC = CD = DE = EF . Найдите отношения AB : CF , AB : BF , BD : AE .

250. Найдите углы, образованные при пересечении двух прямых, если один из них на 42° больше половины второго угла.

Наблюдайте, рисуйте, конструируйте, фантазируйте

251. Разрежьте прямоугольник размером 4 × 9 на две равные части, из которых можно сложить квадрат.

💥 Видео

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

№158. Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой сторонеСкачать

№260. Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторонаСкачать

№158. Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. НайдитеСкачать