В треугольнике высота bh

Задание 6. В треугольнике ABC угол C равен 90°, CH – высота, BH=12, sinA=2/3. Найдите AB.

Углы A и BCH равны как углы со взаимно перпендикулярными сторонами. Выразим AB через синус угла A как

.

Из прямоугольного треугольника BCH видно, что

.

,

Видео:В треугольнике ABC проведены медиана BM и высота BH. Известно, что AC = 2 и BC = BM. Найдите AHСкачать

В треугольнике ABM высота BH делит сторону AM пополам, и равна 5 см?

Геометрия | 5 — 9 классы

В треугольнике ABM высота BH делит сторону AM пополам, и равна 5 см.

Периметр треугольника ABH = 15 см.

Найдите периметр треугольника ABM!

Помогите пожалуйста, есть рисунок !

Решение в скане.

Видео:В треугольнике ABC AC=BC=27, AH — высота, sin BAC= 2/3 . Найдите BH.Скачать

В равнобедренном треугольнике АВС с боковыми сторонами АВ и BC проведена высота BM = 4cм?

В равнобедренном треугольнике АВС с боковыми сторонами АВ и BC проведена высота BM = 4cм.

Найдите периметр треугольника ABM (в сантиметрах), если периметр треугольника ABC равен 20 см.

Видео:В треугольнике ABC BM – медиана и BH – высота ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Задача№2) В треугольнике ABC проведена биссекртиса AD, AD = DC, угол С = 20 градусов?

Задача№2) В треугольнике ABC проведена биссекртиса AD, AD = DC, угол С = 20 градусов.

Найти углы треугольника ABC и ADC /

Задача№3)В прямоугольном треугольнике гипотенуза равна 60 см.

Найти медиану проведённую к гипотенузе.

Задача№4) В треугольнике ABM высота BH делит сторону AM пополам и равна 5 см.

Периметр треугольника ABH = 15 см.

Найти : Периметр треугольника ABM.

Видео:ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

В треугольнике высота BH делит сторону АМ пополам и равна 5 см?

В треугольнике высота BH делит сторону АМ пополам и равна 5 см.

Периметр треугольника АВН равен 15см.

Найти периметр треугольника АВМ.

Видео:В треугольнике ABC AC = BC, AH – высота, AB = 5, sinBAC = 7/25 . Найдите BH.Скачать

В равнобедренном треугольнике ABC с основанием BC проведена медиана AM найдите медиану AM если периметр треугольника ABC равен 32 см а периметр треугольника ABM равен 24 см?

В равнобедренном треугольнике ABC с основанием BC проведена медиана AM найдите медиану AM если периметр треугольника ABC равен 32 см а периметр треугольника ABM равен 24 см.

Видео:16)В остроугольном треугольнике ABC проведена высота BH, угол BAC=48°. Найдите угол ABH. Ответ дайтеСкачать

Треугольник периметр которого 24 высотой делится на 2 треугольника периметры которых равны 14 и 18?

Треугольник периметр которого 24 высотой делится на 2 треугольника периметры которых равны 14 и 18.

Найдите высоту данного треугольника.

Видео:В треугольнике ABC угол С=90, CH -- высота, AB=13, tgA=5. Найти BHСкачать

В равнобедренном треугольнике ABC (AB = BC) проведена высота BM?

В равнобедренном треугольнике ABC (AB = BC) проведена высота BM.

Найти её длину если периметр треугольника ABC равен 70, а периметр треугольника ABM равен 50.

Видео:В треугольнике ABC BM – медиана и BH – высота ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

В треугольнике высота BH делит сторону AM пополам и равна 5 см, периметр треугольника ABH равен 15 см найдите периметр треугольника ABM?

В треугольнике высота BH делит сторону AM пополам и равна 5 см, периметр треугольника ABH равен 15 см найдите периметр треугольника ABM.

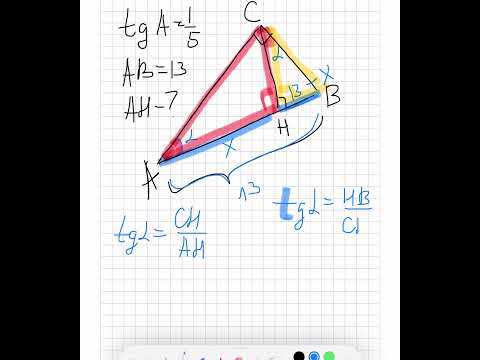
Видео:В треугольнике ABC угол C равен 90°, CH – высота, AB = 13, тангенс A =1/5. Найдите AH.Скачать

№1 Треугольник, периметр которого равен 36, делится высотой на два треугольника, периметры которых равны 18 и 24?

№1 Треугольник, периметр которого равен 36, делится высотой на два треугольника, периметры которых равны 18 и 24.

Найдите высоту этого треугольника.

№2 Треугольник , периметр которого равен 36, делится биссектрисой на два треугольника, периметры которых равны 24 и 30 .

Найдите Биссектрису этого треугольника №3 Периметр равнобедренного треугольника равен 28 см, а основание этого треугольника на 4 см больше боковой стороны.

Найдите стороны этого треугольника Помагите плз!

Срочно и если можно с тертежом.

Видео:Досрочный ОГЭ Математика. Задание 16.Скачать

В равнобедренном треугольнике ABC (AB = BC) проведена высота BM?

В равнобедренном треугольнике ABC (AB = BC) проведена высота BM.

Найти её длину , если периметр треугольника ABC равен 70, а периметр треугольника ABM равен 50.

Видео:Задача 6 №27357 ЕГЭ по математике. Урок 46Скачать

Найдите периметр треугоника ABC (AB = BC), если медиана BM = 11см Периметр треугольника ABM равен 34 см?

Найдите периметр треугоника ABC (AB = BC), если медиана BM = 11см Периметр треугольника ABM равен 34 см.

Если вам необходимо получить ответ на вопрос В треугольнике ABM высота BH делит сторону AM пополам, и равна 5 см?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Угол ЕАС РАВЕН 37 ТК ТРЕУГОЛЬНИК АЕС РАВНОБЕДРЕННЫЙ БАЕ = ЕАС = 37 ТК СУММА УГЛОВ В ТРЕУГОЛЬНИКЕ 180 А УГОЛ БАЕ = БЕА, ТО 180 — 37 — 37 = 106 УГОЛ ВБЕ = 180 — 106 = 74 ТК СМЕЖНЫЕ.

ACB = 180 — (ABC + BAC) = 180 — (ABC + 2LAC) = 180 — (54 + 2×24) = 180 — 102 = 78.

180 * (n — 2) 180 * (5 — 2) = 180 * 3 = 540 ответ : а)540.

Предположим, что 0 0 Если брать другой промежуток, то может быть и отрицательное значение. Cos2a = 2cos²a — 1 1 + tg²a = 1 / cos²a 1 / (1 + tg²a) = cos²a 2cos²a = 2 / (1 + tg²a) 2cos²a — 1 = 2 / (1 + tg²a) — 1 cos2a = 2 / (1 ..

1. Спирогира одна из наиболее распространенных водорослей пресных вод всех частей света, встречается также и в солоноватых водах. Спирогира образует большие ватообразные скопления, которые плавают на поверхности воды или стелются по дну и очень част..

Не понял, что именно надо найти, но : #1 угол АВС равен 180° — 67°32, по свойству смежных углов, угол АВС равен 112, 68° #2 угол 4 равен углу , по свойству вертикальных углов, угол 1 равен 180° — 37° = 143° по свойству смежных углов, угол 3 равен 143..

Координаты векторов АВ(6 ; 8) ВА( — 6 ; — 8).

Пусть переменная х — меньший угол, а 4х — больший угол а сумма этих смежных углов 180 тогда имеем уравнение вида : х + 4х = 180 5х = 180 х = 36 = меньший угол = >больший угол = = 4 * 36 = 144 угол, образующийся за счет биссектрис смежных углов = поло..

M = (a + b) / 2 m = (7 + 12) / 2 m = 9. 5 скобки не нужны.

Видео:Высота BH ромба делит его сторону AD на отрезки ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

16. Планиметрия

Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.

Примеры ответов: 7 или здесьисейчас или 3514

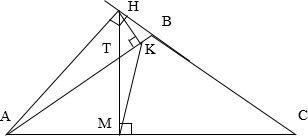
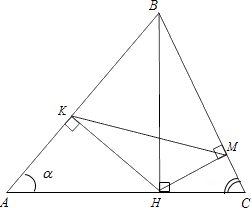
В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.

а) Докажите, что отрезки AM и MK равны.

б) Найдите MK, если AB=5, AC=8.

Пусть $angle BAC=angle BCA=alpha .$ Тогда $angle ABC=180^-2alpha .$

$angle HBA=180^-180^+2alpha =2alpha $ как смежный с $angle ABC.$

Так как треугольник $AHB$ — прямоугольный, то $angle HAB=90^-2alpha .$

$angle HAC=angle HAB+angle BAC=90^-alpha .$

Так как треугольник $AHM$ — прямоугольный, то $angle AHM=90^-90^+alpha =alpha .$

Аналогично из прямоугольго треугольника $HKB$ получаем, что $angle BHK=90^-2alpha .$

Рассмотрим $angle AHB=90^=angle AHM+angle THK+angle BHK=alpha +angle THK+90^-2alpha Rightarrow angle THK=alpha .$

В треугольниках $ATM$ и $HTK$ $angle TAM=angle THK$ по доказанному, $angle AMT=angle HKT=90^$ по условию. Значит, данные треугольники подобны по призкаку подобия по 2 углам. Следовательно,

$displaystyle frac=displaystyle fracRightarrow displaystyle frac=displaystyle frac.$

В треугольнике $ATH$ и $MTK$ $angle ATH=angle MTK$ как вертикальные, $displaystyle frac=displaystyle frac$ по доказанномую Значит, данные треугольники подобны по 2 пропорциональнымсторонам и углу между ними. Тогда, $angle AHT=angle TKM=alpha .$

Получили, что в треугольнике $AKM$ углы при стороне $AK$ равны, значит, треугольник — равнобедренный и $AM=KM.$

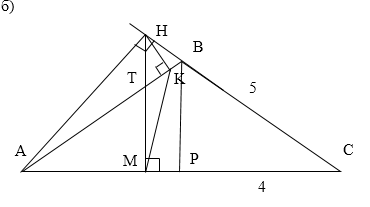
Проведем прямую $BP//HM.$ В равнобедренном треугольнике $ABC$ отрезок $BP$ будет являться высотой и медианой, поэтому $PC=4.$ По теорем е Пифагора $BP^=sqrt<BC^-PC^>=3.$

Прямая $BP$ отсекает от треугольника $HCM$ подобные ему треугольник $BCP,$ поэтому $displaystyle frac=displaystyle frac,$

$displaystyle frac=displaystyle fracRightarrow HC=displaystyle fracCM.$

Обозначим $CM=x,$ тогда $HC=displaystyle fracx,$ $BH=displaystyle fracx-5,$ $AM=8-x.$

Из треугольника $ABH$ по теореме Пифагора $AH^=AB^-BH^=25-(displaystyle fracx-5)^=displaystyle fracx-displaystyle fracx^.$

Аналогично из треугольника $AHC$ $AC^=AH^+HC^$

$64=displaystyle fracx-displaystyle fracx^+displaystyle fracx^$

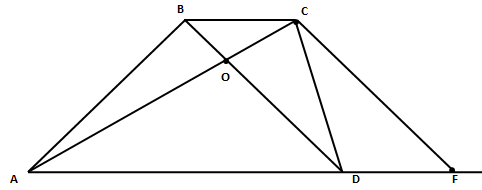
Дана трапеция с диагоналями равными 6 и 8. Сумма оснований равна 10.

а) Докажите, что диагонали перпендикулярны.

б) Найдите высоту трапеции.

а) Проведем прямую CF//BD, тогда BCFD – параллелограмм и BC = DF, CF = BD.

В треугольнике ACF AC = 8, CF = 6, AF = AD + DF = 10.

Если диагонали перпендикулярны, то треугольник ACF – прямоугольный и выполняется теорема Пифагора:

Значит, угол между диагоналями равен 90⁰.

б) $S_=displaystyle fraccdot h=5h,$ , где h – длинна высоты.

С другой стороны $S_=displaystyle fraccdot BDcdot ACcdot sin 90^=24$

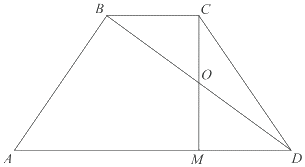
Дана равнобедренная трапеция, в которой AD = 3BC, CM — высота трапеции.

а) Доказать, что M делит AD в отношении 2:1.

б) Найдите расстояние от точки C до середины BD, если AD = 18, $AC=4sqrt.$.

а) Поскольку ABCD — равнобедренная трапеция, то

$MD=displaystyle frac=displaystyle frac=BC$

Тогда $AM=2BC$. Следовательно, $displaystyle frac=displaystyle frac$

Треугольник AMC прямоугольный. В нем $AM=displaystyle fracAD=12$ по доказанному в пункте а) и $AC=4sqrt$ по условию.

По теореме Пифагора $CM^+AM^=AC^$ , откуда $CM=8$ .

Треугольники BCO и MOD равны по катету и острому углу (BC=MD по доказанному в пункте а) , углы CBO и ADO равны как накрест лежащие). Тогда BO = OD и СO = OM как соответственные элементы равных треугольников. Значит, СO — искомое расстояние.

В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.

а) Докажите, что треугольник MBK подобен треугольнику ABC.

б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.

а) Обозначим $angle BAC=alpha .$. Треугольники AKH, CMH, ABH и BKH – прямоугольные. Тогда $angle KHA=angle ABH=90^-alpha .$. Аналогично $angle KHB=90^-(90^-alpha )=alpha .$. В четырехугольнике BKHM $angle BKH+angle BMH=90^+90^=180^,$, значит, вокруг этого четырехугольника можно описать окружность. Углы $angle KHB=angle KMB=alpha $ как опирающиеся на одну и ту же хорду.

В треугольниках ABC и MKB $angle KMB=angle BAC,angle ABC$ — совпадающий. Значит, они подобны по признаку подобия по 2 углам.

б) Обозначим k – коэффициент подобия треугольников ABC и MKB (k

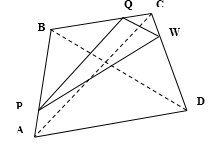
Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB=CQ:QB=CW:WD=1:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ=16, QW=12, угол PWQ — острый.

а) Докажите, что треугольник PQW — прямоугольный.

б) Найдите площадь четырёхугольника ABCD.

а) По теореме синусов из треугольника $PQW:$

$sin angle PWQ=displaystyle frac,sin angle QPW=displaystyle frac.$

Заметим, что $sin ^angle PWQ+sin ^angle QPW=displaystyle frac+displaystyle frac=1.$

$sin ^angle QPW=cos ^angle PWQ,$

$sin angle QPW=cos angle PWQ,$

так как угол $QWP$ — острый. Тогда $angle QPW+angle PWQ=90^$ и треугольник $PQW$ — прямоугольный.

б) Треугольник $PBQ$ и $ABC$ подобные по двум стронам и углу между ими ($angle B$ — общий, $displaystyle frac=displaystyle frac=displaystyle frac).$ Значит, $ACparallel PQ$ и $AC=displaystyle fracPQ=20.$

Аналогично, из подобия треугольников $QCW$ и $BCQ$ получаем, что $BDparallel QW$ и $BD=5QN=60$

Угол между прямыми $BD$ и $AC$ равен углу между прямыми $PQ$ и $QW,$ поэтому

$S_=displaystyle fracBDcdot ACcdot sin 90^=displaystyle frac60cdot 20=600.$

📺 Видео

В треугольнике ABC AB=BC, а высота AH делит сторону BC ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

В остроугольном треугольнике ABC высота AH равна 9√69 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Задание 6 ЕГЭ по математике. Урок 26Скачать

Задачи на доказательства по геометрии 24 номер ОГЭСкачать

Вычисляем высоту через координаты вершин 1Скачать

15 задание ОГЭ по математике 2023 Треугольник Shorts #shorts #огэпоматематике2023 #треугольникСкачать

В треугольнике ABC угол C равен 90°, CH – высота, AC = 3, cos A =1/6. Найдите BH.Скачать

Задача 6 №27358 ЕГЭ по математике. Урок 47Скачать