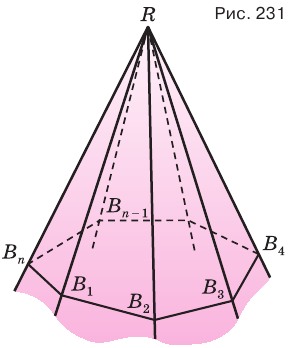
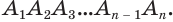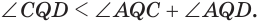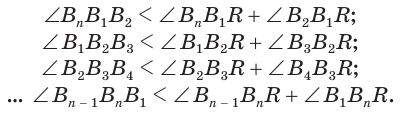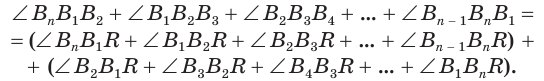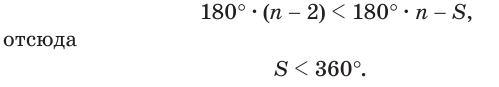Многогранник с гранями треугольниками (7 видео)

Правильные многогранники в геометрии с примерами

Пусть есть плоский многоугольник

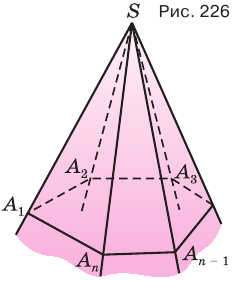
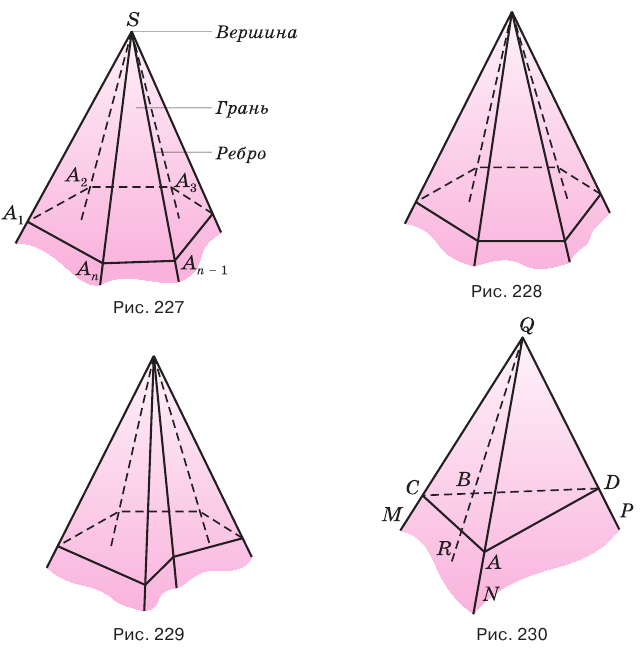
Многогранный угол называется выпуклым, если он расположен по одну сторону от плоскости любой его грани. Многогранный угол на рисунке 228 выпуклый, а на рисунке 229 — невыпуклый. По количеству граней многогранные углы разделяют на трехгранные, четырехгранные и т. д.

Теорема 12.

Сумма плоских углов выпуклого многогранного угла меньше 360°.

Доказательство:

Установим сначала, что каждый плоский угол трехгранного угла меньше суммы двух других его углов.

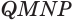
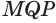
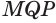
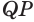
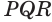
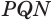
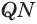
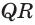
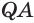
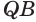
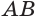
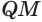
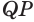
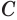
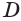
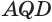
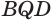
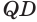
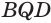
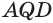
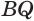
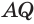
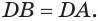
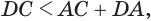
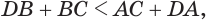
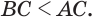
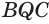
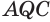
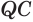
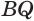
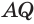
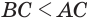
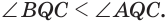
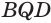
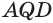
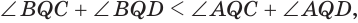
Пусть есть трехгранный угол (рис. 230). Пусть для определенности угол — больший из плоских углов трехгранного угла. В плоскости грани от луча отложим угол , равный углу , и на лучах и отложим равные отрезки и . Через прямую проведем такую плоскость, которая пересекает ребра и в некоторых точках и . Треугольники и равны, так как у них сторона общая, и по построению равны углы и , а также стороны и . Значит, Далее по свойству сторон треугольника получаем или или Теперь, поскольку у треугольников и сторона общая, стороны и равны, но , то Прибавив к левой и правой частям этого неравенства соответственно углы и , которые равны друг другу, получим, что или

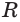
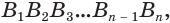
Пусть теперь есть выпуклый многогранный угол с вершиной (рис. 231). Если пересечь его какой-либо плоскостью, то в сечении получим многоугольник каждая вершина которого является вершиной трехгранного угла, образованного двумя гранями данного угла и секущей плоскостью. По доказанному для этих трехгранных углов получаем:

Сложим покомпонентно эти неравенства:

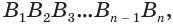
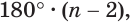
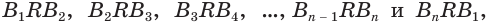
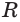
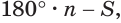
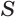
Теперь обратим внимание на то, что сумма в левой части последнего неравенства есть сумма углов многоугольника которая равна а в правой — сумма углов всех треугольников но без их углов при вершине , которая равна где выражает сумму плоских углов данного многогранного угла. Таким образом,

Многогранник, у которого все грани являются равными правильными многоугольниками и все двугранные углы равны друг другу, называется правильным многогранником.

Из этого определения следует, что у правильного многогранника равны друг другу все его:

Теорема 13.

Количество ребер, сходящихся в каждой вершине правильного многогранника, не больше пяти.

Доказательство:

Допустим, что это не так, т. е. в вершине многогранника сходится шесть или больше ребер. Тогда при этой вершине многогранник имел бы шесть или больше равных плоских углов. Учитывая, что сумма этих углов меньше 360°, получаем, что каждый из них меньше 60°. Но это невозможно, поскольку гранями правильного многогранника являются правильные многоугольники, а у них углы не меньше 60°.

Теорема 14.

Количество сторон правильного многоугольника, являющегося гранью правильного многогранника, не больше пяти.

Доказательство:

В каждой вершине правильного многогранника сходится не менее трех плоских углов, а поэтому каждый из них должен быть меньше 120°. Вместе с этим угол правильного шестиугольника равен 120°, а угол правильного многоугольника с большим количеством сторон больше 120°. Поэтому правильные многоугольники, количество сторон которых больше пяти, не могут быть гранями правильного многоугольника.

Теорема 15.

Есть пять типов правильных многогранников.

Доказательство:

В соответствии с теоремой 14 гранями многогранника могут быть правильные треугольники, четырехугольники или пятиугольники.

Если гранями правильного многогранника служат треугольники, то, с учетом теоремы 13, в вершинах многогранника могут сходиться три, четыре или пять ребер. Если гранями правильного многогранника служат четырехугольники или пятиугольники, то в вершинах многогранника может сходиться только три ребра. Значит, существует не более пяти видов правильных многогранников.

Чтобы убедиться, что такие виды многогранников существуют, достаточно указать способ построения каждого из них.

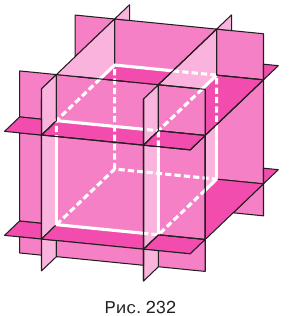
Прежде всего отметим, что правильным многогранником, гранями которого служат правильные четырехугольники, т. е. квадраты, является куб, который еще называют правильным гексаэдром. Куб можно построить так. В произвольно выбранной плоскости построить квадрат, через его стороны провести плоскости, перпендикулярные выбранной плоскости, и провести еще одну плоскость, параллельную выбранной плоскости и отстоящую от нее на сторону квадрата (рис. 232). Мы видим, что гексаэдр имеет 6 граней, 12 ребер и 8 вершин.

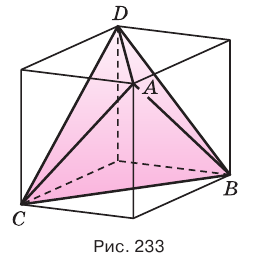
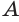
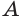
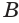
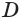
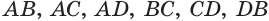
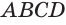
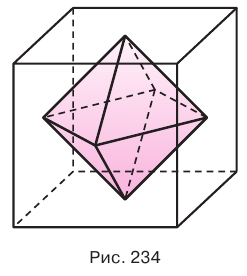
Построение многогранника, в каждой вершине которого сходится по три треугольные грани, может быть таким. Построить куб. Выбрать одну из его вершин и в каждой грани с этой вершиной выбрать вершину, противолежащую вершине . Пусть это вершины , , . Точки , , , являются вершинами искомого многогранника (рис. 233). Действительно, каждый из отрезков является диагональю одной из граней куба, а поэтому все эти отрезки равны друг другу. Получается, что в треугольной пирамиде все грани являются правильными треугольниками. Такая пирамида называется правильным тетраэдром. Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.

Построение многогранника, в каждой вершине которого сходится по четыре треугольные грани, может быть таким. Построить куб и найти центры шести его граней (рис. 234). Эти точки являются вершинами многогранника, все грани которого — правильные треугольники. Такой многогранник называется правильным октаэдром. Октаэдр имеет 8 граней, 12 ребер и 6 вершин.

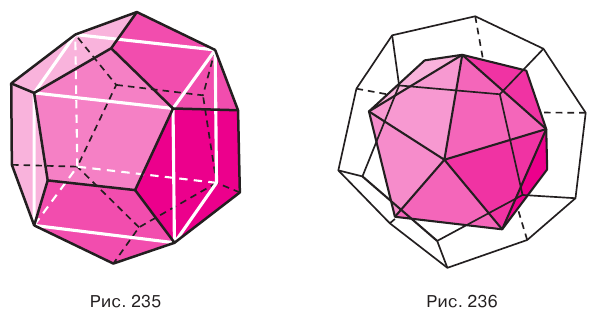
Построение многогранника, в каждой вершине которого сходится по три пятиугольные грани, можно выполнить, снова используя куб. Если через каждое из двенадцати ребер куба провести плоскость, которая не имеет с поверхностью куба других общих точек, кроме точек этого ребра, то полученные 12 плоскостей при пересечении дадут грани некоторого многогранника. Можно так подобрать наклон этих плоскостей к граням куба, что грани этого двенадцатигранника будут правильными пятиугольниками (рис. 235). Такой многогранник называется правильным додекаэдром. Додекаэдр имеет 12 граней, 30 ребер и 20 вершин.

Наконец, многогранник, в каждой вершине которого сходится по пять треугольных граней, можно построить, используя додекаэдр: центры граней додекаэдра являются вершинами искомого правильного многогранника (рис. 236). Такой многогранник называется правильным икосаэдром. Икосаэдр имеет 20 граней, 30 ребер и 12 вершин.

Таким образом, есть пять типов правильных многогранников.

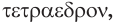
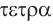
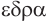
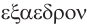
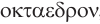
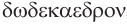
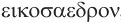
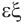
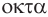
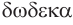
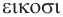
Названия правильных многогранников происходят из греческого языка. Термин тетраэдр, по-гречески означает четырехгранник: — четыре и — грань. Соответственно термины гексаэдр, октаэдр, додекаэдр, икосаэдр, по-гречески , , , , означают шестигранник, восьмигранник, двенадцатигранник, двадцатигранник: , — шесть, — восемь, — двенадцать, — двадцать.

Мы знаем, что правильные гексаэдр и тетраэдр имеют описанный и вписанный шары. Также описанный и вписанный шары имеют октаэдр, додекаэдр и икосаэдр. Центры этих шаров совпадают, и эта точка является центром симметрии соответствующего правильного многогранника, кроме тетраэдра, который не имеет центра симметрии.

Рекомендую подробно изучить предметы:

Геометрия
Аналитическая геометрия
Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

Многогранники
Окружность
Эллипс
Гипербола
Пирамида в геометрии
Конус в геометрии
Сфера в геометрии
Шар в геометрии

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Содержание

Многогранник с гранями треугольниками
Правильные многогранники. Часть 1. Трёхмерие
Введение. Постановка вопроса.
Сфера
Лобачевский
Правильные разбиения двумерной Сферы и правильные трёхмерные многогранники
Построение разбиений двумерной сферы, плоскости Евклида и плоскости Лобачевского
🔥 Видео

Видео:Видеоурок по математике "Понятие правильного многогранника"Скачать

Многогранник с гранями треугольниками

Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники, и в каждой вершине сходится одинаковое число граней.
Рассмотрим возможные правильные многогранники и прежде всего те из них, гранями которых являются правильные треугольники. Наиболее простым таким правильным многогранником является треугольная пирамида, гранями которой являются правильные треугольники (рис. 1,а). В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает четырехгранник.

Многогранник, гранями которого являются правильные треугольники, и в каждой вершине сходится четыре грани, изображен на рисунке 1,в. Его поверхность состоит из восьми правильных треугольников, поэтому он называется октаэдром.
Многогранник, в каждой вершине которого сходится пять правильных треугольников, изображен на рисунке 1,г. Его поверхность состоит из двадцати правильных треугольников, поэтому он называется икосаэдром.
Заметим, что поскольку в вершинах выпуклого многогранника не может сходиться более пяти правильных треугольников, то других правильных многогранников, гранями которых являются правильные треугольники, не существует.
Аналогично, поскольку в вершинах выпуклого многогранника может сходиться только три квадрата, то, кроме куба (рис. 1,б), других правильных многогранников, у которых гранями являются квадраты не существует. Куб имеет шесть граней и поэтому называется также гексаэдром.
Многогранник, гранями которого являются правильные пятиугольники, и в каждой вершине сходится три грани, изображен на рисунке 1,д. Его поверхность состоит из двенадцати правильных пятиугольников, поэтому он называется додекаэдром.
Поскольку в вершинах выпуклого многогранника не могут сходиться правильные многоугольники с числом сторон больше пяти, то, используя теорему Коши о жесткости выпуклого многогранника, получаем, что других правильных многогранников не существует, и таким образом, имеется только пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.
Рассмотрим понятие правильного многогранника с точки зрения топологии науки, изучающей свойства фигур, не зависящих от различных деформаций без разрывов. С этой точки зрения, например, все треугольники эквивалентны, так как один треугольник всегда может быть получен из любого другого соответствующим сжатием или растяжением сторон. Вообще все многоугольники с одинаковым числом сторон эквивалентны по той же причине.
Как в такой ситуации определить понятие топологически правильного многогранника? Иначе говоря, какие свойства в определении правильного многогранника являются топологически устойчивыми и их следует оставить, а какие не являются топологически устойчивыми и их следует отбросить.
В определении правильного многогранника количество сторон и количество граней являются топологически устойчивыми, т.е. не меняющимися при непрерывных деформациях. Правильность же многоугольников не является топологически устойчивым свойством. Таким образом, мы приходим к следующему определению.
Выпуклый многогранник называется топологически правильным, если его гранями являются многоугольники с одним и тем же числом сторон и в каждой вершине сходится одинаковое число граней.
Например, все треугольные пирамиды являются топологически правильными многогранниками, эквивалентными между собой. Все параллелепипеды также являются эквивалентными между собой топологически правильными многогранниками. Четырехугольные пирамиды не являются топологически правильными многогранниками.
Выясним вопрос о том, сколько существует не эквивалентных между собой топологически правильных многогранников.
Как мы знаем, существует только пять правильных многогранников: тетраэдр, куб, октаэдр, икосаэдр и додекаэдр. Казалось бы, топологически правильных многогранников должно быть гораздо больше. Однако оказывается, что никаких других топологически правильных многогранников, не эквивалентных уже известным правильным, не существует.
Для доказательства этого воспользуемся теоремой Эйлера. Пусть дан топологически правильный многогранник, гранями которого являются n — угольники, и в каждой вершине сходится m ребер. Ясно, что n и m больше или равны трем. Обозначим, как и раньше, В — число вершин, Р — число ребер и Г — число граней этого многогранника. Тогда

n Г = 2P; Г = ; mB = 2P; В = .

По теореме Эйлера, В — Р + Г = 2 и, следовательно,

Откуда Р = .
Из полученного равенства, в частности, следует, что должно выполняться неравенство 2n + 2m – nm > 0, которое эквивалентно неравенству (n – 2)(m – 2)
Найдем всевозможные значения n и m, удовлетворяющие найденному неравенству, и заполним следующую таблицу

Видео:Геометрия 10 класс (Урок№13 - Многогранник.)Скачать

Правильные многогранники. Часть 1. Трёхмерие

Видео:Геометрия 10 кл Понятие многогранникаСкачать

Введение. Постановка вопроса.

В школьной программе, к сожалению, сферическую геометрию и геометрию Лобачевского не изучают. Тем временем, их изучение совместно с Евклидовой геометрией, позволяет глубже понять происходящее с объектами. Например, понять связь правильных многогранников с разбиениями сферы, разбиениями плоскости Евклида и разбиениями плоскости Лобачевского.
Знания геометрии пространств постоянной кривизны помогает подниматься над трёхмерием и выявлять многогранники в пространствах размерности 4 и выше. Вопросы нахождения многогранников, нахождения разбиений пространств постоянной кривизны, вывода формулы двугранного угла правильного многогранника в n-мерном пространстве — так тесно переплетены, что выносить всё это в название статьи оказалось проблематично. Пусть в центре внимания будут, всем понятные, правильные многогранники, хотя они не только результат всех выводов, но и, одновременно, инструмент для постижения пространств высших размерностей и равномерно искривлённых пространств.

Для тех кто не знает (забыл) сообщаю (напоминаю), что в привычном нам трёхмерном Евклидовом пространстве всего пять правильных многогранников:

1. Тетраэдр:	2. Куб:	3. Октаэдр:	4. Додекаэдр:	5. Икосаэдр:

В трёхмерном пространстве правильным многогранником называется выпуклый многогранник, у которого все вершины равны между собой, все рёбра равны между собой, все грани равны между собой и грани являются правильными многоугольниками.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.

Вершины равны между собой означает, что количество рёбер и количество граней подходящих к каждой вершине одинаковое и подходят они под одинаковыми углами, в каждой вершине.

Оказывается, правильные многогранники удобно обозначать их символом Шлефли , характеризующим их комбинаторное строение. Который означает, что p1 угольники, сошлись по p2 штук в вершине. Т.е. по определению p1, p2 — целые числа, большие либо равные 3. Для тех кто не знаком с понятием Символ Шлефли написал отдельную статью с картинками Символ Шлефли. Часть 2.6

В такой записи наши многогранники получат обозначения:
1. Тетраэдр ,
2. Куб ,
3. Октаэдр ,
4. Додекаэдр ,
5. Икосаэдр
Например, — куб имеет 4 угольные грани, в каждой вершине сходится по 3 таких грани.
У октаэдра наоборот, грани 3 угольные, сходятся по 4 штуки в вершине.
Таким образом символ Шлефли полностью определяет комбинаторное строение многогранника.

Почему правильных многогранников всего 5? Может быть их больше?

Чтобы сполна дать ответ на этот вопрос, нужно сначала получить интуитивное представление о геометрии на сфере и на плоскости Лобачевского. Тем у кого такого представления ещё нет постараюсь дать необходимые объяснения.

Видео:Икосаэдр из бумаги. Чертёж развертки икосаэдра.Скачать

Сфера

1. Что такое точка на сфере? Думаю, что всем интуитивно понятно. Мысленно не сложно представить точку на сфере.

2. Что такое отрезок на сфере? Берём две точки и соединяем их кратчайшим расстоянием на сфере, получится дуга, если смотреть на сферу со стороны.

3. Если продолжить этот отрезок в обе стороны, то он замкнётся и получится окружность. При этом плоскость окружности содержит центр сферы, это следует из того, что две исходные точки мы соединили кратчайшим, а не произвольным, расстоянием. Это со стороны она выглядит, как окружность, а в терминах сферической геометрии это прямая, так как была получена из отрезка, продолжением до бесконечности в обе стороны.

4. И, наконец, что такое треугольник на сфере? Берём три точки на сфере и соединяем их отрезками.

По аналогии с треугольником можно нарисовать произвольный многоугольник на сфере. Для нас принципиально важно свойство сферического треугольника, заключающееся в том, что сумма углов у такого треугольника больше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных сферических треугольников различна. Чем больше треугольник, тем БОЛЬШЕ у него сумма углов.

Соответственно, появляется 4-й признак равенства треугольников на сфере — по трём углам: два сферических треугольника равны между собой, если у них соответствующие углы равны.

Для простоты саму сферу проще не рисовать, тогда треугольник будет выглядеть немного раздутым:

Сферу ещё называют пространством постоянной положительной кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Лобачевский

Теперь, когда мы познакомились с геометрией на сфере, понять геометрию на гиперболической плоскости, открытую великим русским учёным Николаем Ивановичем Лобачевским, будет тоже не сложно, так как тут всё происходит аналогично сфере, только «наизнанку», «наоборот». Если дуги на сфере мы проводили окружностями, с центром внутри сферы, то теперь дуги надо проводить окружностями с центром за пределами сферы.

Приступим. Плоскость Лобачевского будем представлять в интерпретации Пуанкаре II (Жюль Анри́ Пуанкаре́, великий французский учёный), эту интерпретацию геометрии Лобачевского ещё называют диском Пуанкаре.

1. Точка в плоскости Лобачевского. Точка — она и в Африке точка.

2. Отрезок на плоскости Лобачевского. Соединяем две точки линией по кратчайшему расстоянию в смысле плоскости Лобачевского.

Кратчайшее расстояние строится следующим образом:

Надо провести окружность ортогональную диску Пуанкаре, через заданные две точки (Z и V на рисунке). Центр этой окружности будет находиться всегда за пределами диска. Дуга соединяющая исходные две точки будет кратчайшим расстоянием в смысле плоскости Лобачевского.

3. Убрав вспомогательные дуги, получим прямую E1 — H1 в плоскости Лобачевского.

Точки E1, H1 «лежат» на бесконечности плоскости Лобачевского, вообще край диска Пуанкаре — это всё бесконечно удалённые точки плоскости Лобачевского.

4. И наконец, что такое треугольник в плоскости Лобачевского? Берём три точки и соединяем их отрезками.

По аналогии с треугольником, можно нарисовать произвольный многоугольник на плоскости Лобачевского. Для нас принципиально важно свойство гиперболического треугольника, заключающееся в том, что сумма углов у такого треугольника всегда меньше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных гиперболических треугольников различна. Чем больше треугольник по площади, тем МЕНЬШЕ у него сумма углов.

Соответственно, тут тоже имеет место 4-й признак равенства гиперболических треугольников — по трём углам: два гиперболических треугольника равны между собой, если у них соответствующие углы равны.

Для простоты сам диск Пуанкаре иногда можно не рисовать, тогда треугольник будет выглядеть немного «усохшим», «сдутым»:

Плоскость Лобачевского (и вообще пространство Лобачевского любой размерности) ещё называют пространством постоянной ОТРИЦАТЕЛЬНОЙ кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.

Видео:Правильные и полуправильные многогранникиСкачать

Правильные разбиения двумерной Сферы и правильные трёхмерные многогранники

Всё сказанное про сферу и плоскость Лобачевского относится к двумерию, т.е. поверхность сферы — двумерна. Какое это имеет отношению к трёхмерию, указанному в заголовке статьи? Оказывается, каждому трёхмерному правильному Евклидову многограннику взаимно однозначно соответствует своё разбиение двумерной сферы. Лучше всего это видно на рисунке:

Чтобы из правильного многогранника получить разбиение сферы, нужно описать вокруг многогранника сферу. Вершины многогранника окажутся на поверхности сферы, соединив эти точки отрезками на сфере (дугами), получим разбиение двумерной сферы на правильные сферические многоугольники. Для примера сделана видео демонстрация как икосаэдр соответствует разбиению сферы на сферические треугольники и обратно, как разбиение сферы на сферические треугольники, сходящиеся по пять штук в вершине, соответствует икосаэдру.

Чтобы по разбиению сферы построить многогранник, соответствующие дугам вершины разбиения нужно соединить обычными, прямолинейными, Евклидовыми отрезками.

Соответственно символ Шлефли икосаэдра — трёхугольники, сходящиеся по пять штук в вершине, задаёт не только структуру этого многогранника, но и структуру разбиения двумерной сферы. Аналогично и с другими многогранниками, их символы Шлефли задают и структуру соответствующих разбиений. Более того, разбиения плоскости Евклида и плоскости Лобачевского на правильные многоугольники, тоже можно задавать символом Шлефли. Например, — четырёхугольники, сходящиеся по четыре — это всем привычная нам тетрадь в клеточку, т.е. это разбиение плоскости Евклида на квадраты. А есть ли другие разбиения плоскости Евклида? Увидим дальше.

Видео:Икосаэдр из бумаги/Paper icosahedron/Правильный многогранник/DIYСкачать

Построение разбиений двумерной сферы, плоскости Евклида и плоскости Лобачевского

Для построения разбиений двумерных пространств постоянной кривизны (таково общее название этих трёх пространств) нам потребуется элементарная школьная геометрия и знание того, что сумма углов сферического треугольника больше 180 градусов (больше Пи), что сумма углов гиперболического треугольника меньше 180 градусов (меньше Пи) и что такое символ Шлефли. Обо всём об этом уже сказано выше.

Итак, возьмём произвольный символ Шлефли , он задаёт разбиение одного из трёх пространств постоянной кривизны (для плоскости это верно, для пространств высших размерностей дело обстоит сложнее, но ничто нам не мешает исследовать все комбинации символа).

Рассмотрим правильный p1 угольник, проведём отрезки, соединяющие его центр и вершины. Получим p1 штук равнобедренных треугольника (на рисунке показан только один такой треугольник). Сумму углов каждого из этих треугольников обозначим за t и выразим t через пи и коэффициент лямда.

Тогда если лямда = 1, то треугольник Евклидов, т.е. находится в Евклидовой плоскости, если лямда в интервале (1, 3), то это значит, что сумма углов больше пи и значит этот треугольник сферический (не трудно представить, что при увеличении сферического треугольника в пределе получается окружность с тремя точками на ней, в каждой точке угол треугольника получается равным пи, а в сумме 3*пи. Это объясняет верхнюю границу интервала = 3). Если же лямда в интервале (0, 1), то треугольник гиперболический, так как сумма углов у него меньше пи (т.е. меньше 180 градусов). Коротко это можно записать так:

Не трудно посчитать, что:

С другой стороны, для сходимости в вершине p2 штук (т.е. целого числа) таких же многоугольников нужно, чтобы

Приравнивая выражения для 2*бетта, найденные из условия сходимости и из многоугольника:

Получили уравнение которое показывает какое из трёх пространств разбивает фигура заданная своим символом Шлефли . Для решения этого уравнения надо вспомнить, так же, что p1, p2 — целые числа, большие либо равные 3. Это, так сказать, следует из их физического смысла, так как это p1 угольники (не меньше 3 углов), сходящиеся по p2 штук в вершине (тоже не меньше 3, иначе это не вершина получится).

Решение этого уравнения заключается в переборе всех возможных значений для p1, p2 больших либо равных 3 и вычислении значения лямда. Если оно получится равным 1, то разбивает плоскость Евклида, если больше 1 но меньше 3, то это разбиение Сферы, если от 0 до 1, то это разбиение плоскости Лобачевского. Все эти вычисления удобно свести в таблицу.

Откуда видно, что:
1. Сфере соответствует всего 5 решений, когда лямда больше 1 и меньше 3, они выделены зелёным цветом в таблице. Это: — тетраэдр, — октаэдр, — икосаэдр, — куб, — додекаэдр. Их картинки были представлены в начале статьи.
2. Разбиениям Евклидовой плоскости соответствует всего три решения, когда лямда = 1, они выделены синим цветом в таблице. Вот как выглядят эти разбиения.

3. И наконец, все остальные комбинации соответствуют разбиениям плоскости Лобачевского, соответственно таких разбиений бесконечное (счётное) количество. Осталось только проиллюстрировать некоторые из них, для примера.