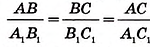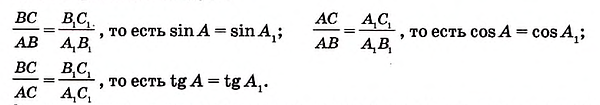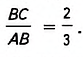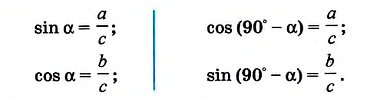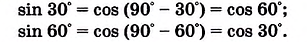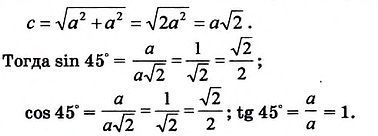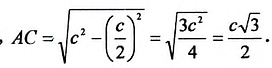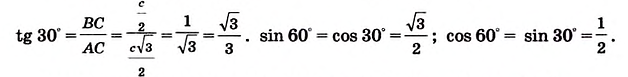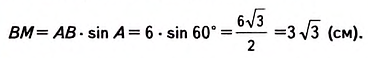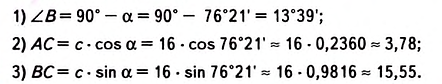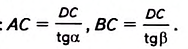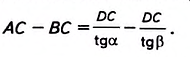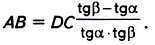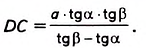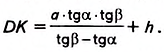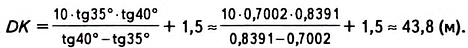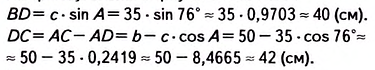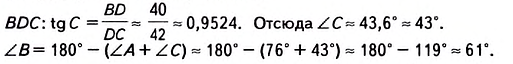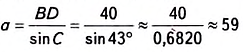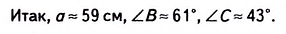Основные метрические сооьтношения в прямоугольном треугольнике
- §1. Прямоугольный треугольник. Метрические соотношения.
- Метрические соотношения в треугольнике
- § 16. Теорема Пифагора.
- § 17. Тригонометрические функции острого угла прямоугольного треугольника.
- § 18. Решение прямоугольных треугольников.
- ИТОГИ ГЛАВЫ 3
- Решение прямоугольных треугольников с формулами и примерами вычисления
- Метрические соотношения в прямоугольном треугольнике
- Теорема Пифагора
- Тригонометрические функции острого угла прямоугольного треугольника
- Решение прямоугольных треугольников
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Четырехугольник, его элементы. Сумма углов четырехугольника
- Пример №5
- Пример №6
- Пример №7
- Пример №8
- Пример №9
- Пример №10
- Пример №11
- Перпендикуляр и наклонная, их свойства
- Пример №12
- Пример №13
- Синус, косинус и тангенс острого угла прямоугольного треугольника. Соотношения между сторонами и углами в прямоугольном треугольнике
- Пример №14
- Пример №15
- Пример №16
- Пример №17
- Вычисление прямоугольных треугольников
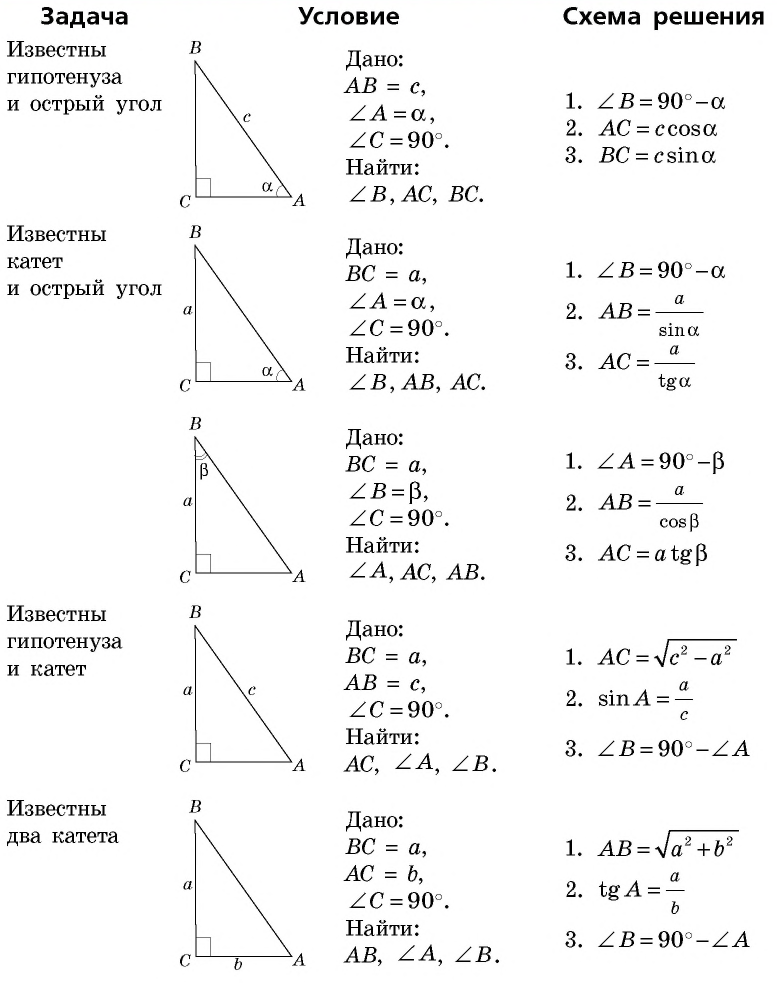
- Решение прямоугольных треугольников по гипотенузе и острому углу
- Решение прямоугольных треугольников по катету и острому углу
- Решение прямоугольных треугольников по двум катетам
- Решение прямоугольных треугольников по катету и гипотенузе
- Определение прямоугольных треугольников
- Синус, косинус и тангенс
- Пример №18
- Тригонометрические тождества
- Пример №19
- Вычисление значений тригонометрических функций. Формулы дополнения
- Значения тригонометрических функций углов 30 45 60
- Решение прямоугольных треугольников
- Нахождение неизвестных сторон прямоугольного треугольника
- Пример №20
- Примеры решения прямоугольных треугольников
- Пример №21
- Пример №22
- Пример №23
- Пример №24
- Пример №25
- Пример №26
- Историческая справка
- Приложения
- Теорема (обобщенная теорема Фалеса)
- Теорема (формула площади прямоугольника)
- Золотое сечение
- Пример №27
- Пример №28
- Пример №29
- Вычисление значений sin a, cos а и tg а
- Пример №31
- Как решать прямоугольные треугольники
- Пример №32
- Пример №33
- Пример №34
- Пример №35
- Пример №36
- Пример №37
- 📸 Видео
§1. Прямоугольный треугольник. Метрические соотношения.
Основные метрические сооьтношения в прямоугольном треугольнике
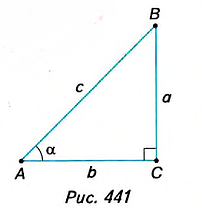
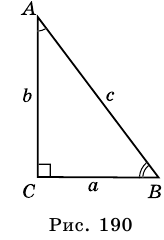
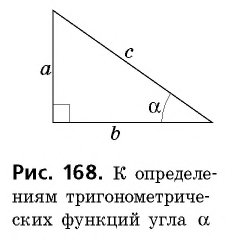
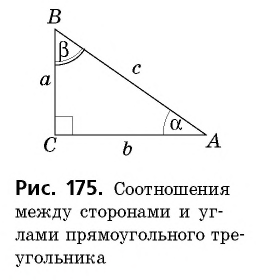
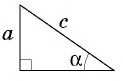
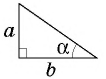
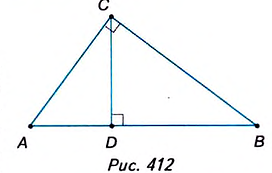
Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).
Используем обычные обозначения:
`c` — гипотенуза `AB`;
`a` и `b` – катеты `BC` и `AC` (по-гречески «kathetos — катет» означает отвес, поэтому такое изображение прямоугольного треугольника нам представляется естественным);
`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;
`h` – высота `CD`, опущенная на гипотенузу;
`m_c` – медиана `CM`, проведённая к гипотенузе;
`R` – радиус описанной окружности;
`r` – радиус вписанной окружности.
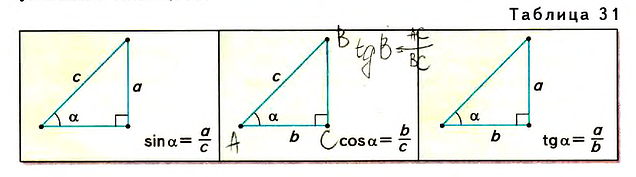
Напомним, что если `alpha` — величина острого угла `A` прямоугольного треугольника `ABC` (см. рис. 1), то
`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.
Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.
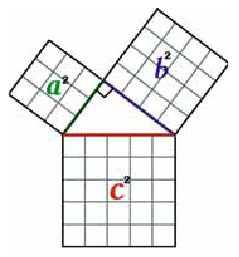
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
`c^2 = a^2 + b^2`
Доказательство теоремы повторите по учебнику.
Выведем ряд соотношений между элементами прямоугольного треугольника.
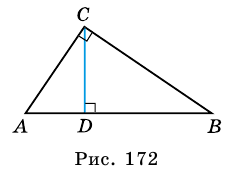
Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу
Если `/_ A = alpha` (см. рис. 1), то `/_ CBD = 90^@ — alpha` и `/_ BCD = alpha`. Из треугольника `ABC` `sin alpha = (BC)/(AB)`, а из треугольника `BCD` `sin alpha = (BD)/(BC)`.
Значит, `(BC)/(AB) = (BD)/(BC)`, откуда `BC^2 = AB * BD`, т. е. `a^2 = c * a_c` . Аналогично доказывается второе равенство.
Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу
Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.
Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.
Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу
Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.
Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.
Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.
Пусть `AM = BM`. Проведём $$ MKVert BC$$ (рис. 2), тогда по теореме Фалеса `AK = CK`
.
Кроме того, из того, что `BC _|_ AC` и $$ MKVert BC$$ следует `MK _|_ AC`. В прямоугольных треугольниках `CMK` и `AMK` катет `MK` общий, катеты `CK` и `AK` равны. Эти треугольники равны и `CM = AM`, т. е. `CM = 1/2 AB`.
Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы
Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.
Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей
`a + b = 2(R + r)` или `a + b = c + 2r`
Пусть `O` — центр вписанной окружности и `F`, `N` и `S` — точки касания сторон треугольника `ABC` (рис. 3), тогда `OF_|_ BC`, `ON _|_ AC`, `OS _|_ AB` и `OF = ON = OS = r`. Далее, `OFCN` — квадрат со стороной `r`, поэтому `BF = BC — FC`, `AN = AC — CN`, т. е. `BF = a — r` и `AN = b — r`.
Прямоугольные треугольники `AON` и `AOS` равны (гипотенуза `AO` — общая, катеты `ON` и `OS` равны), следовательно, `AS = AN`, т. е. `AS = b — r`.
Аналогично доказывается, что `BS = a — r`, поэтому из `AB = AS + BS` следует `c = (b — r) + (a — r)`, т. е. `a + b = c + 2r`. Зная, что `c = 2R`, окончательно получаем `a + b = 2(R + r)`.
Равенства, доказанные в Свойствах 1 и 2, записываются также как:
Видео:МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ . §15 геометрия 8 классСкачать

Метрические соотношения в треугольнике
§ 16. Теорема Пифагора.
§ 17. Тригонометрические функции острого угла прямоугольного треугольника.
§ 18. Решение прямоугольных треугольников.
ИТОГИ ГЛАВЫ 3
Метрические соотношения в прямоугольном треугольнике
Квадрат высоты прямоугольного треугольника, проведённой к гипотенузе, равен произведению проекций катетов на гипотенузу. Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Синус острого угла прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника
Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника
Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.
Котангенс острого угла прямоугольного треугольника
Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему.
Тригонометрические формулы
Соотношения между сторонами и значениями тригонометрических функций углов в прямоугольном треугольнике
- Катет прямоугольного треугольника равен произведению гипотенузы на синус угла, противолежащего этому катету.
- Катет прямоугольного треугольника равен произведению гипотенузы на косинус угла, прилежащего к этому катету.
- Катет прямоугольного треугольника равен произведению второго катета на тангенс угла, противолежащего первому катету.
- Катет прямоугольного треугольника равен произведению второго катета на котангенс угла, прилежащего к первому катету.
- Гипотенуза прямоугольного треугольника равна частному от деления катета на синус противолежащего ему угла.
- Гипотенуза прямоугольного треугольника равна частному от деления катета на косинус прилежащего к нему угла.
«Мерзляк Геометрия 8 Глава 3» СОДЕРЖАНИЕ: § 15. Метрические соотношения в прямоугольном треугольнике. § 16. Теорема Пифагора. § 17. Тригонометрические функции острого угла прямоугольного треугольника. § 18. Решение прямоугольных треугольников.
Это конспект по теме «Мерзляк Геометрия 8 Глава 3». Выберите дальнейшие действия: Вернуться к Списку конспектов по геометрии.
Видео:Метрические соотношения в прямоугольном треугольнике. 1 часть. 9 класс.Скачать

Решение прямоугольных треугольников с формулами и примерами вычисления
Содержание:
В этой лекции вы ознакомитесь со знаменитой теоремой Пифагора. Вы научитесь по известным сторонам и углам прямоугольного треугольника находить его неизвестные стороны и углы.
Видео:Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Метрические соотношения в прямоугольном треугольнике
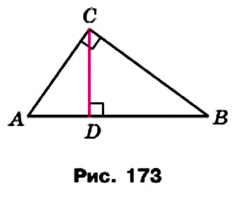
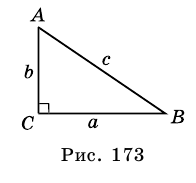
На рисунке 173 отрезок CD — высота прямоугольного треугольника ABC
Отрезки AD и DB называют проекциями катетов АС и СВ соответственно на гипотенузу.
Лемма. Высота прямоугольного треугольника, проведенная к гипотенузе делит треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Докажите лемму самостоятельно.
Теорема 15.1. Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу. Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.
Доказательство. На рисунке 173 отрезок CD — высота прямоугольного треугольника ABC
Докажем, что
- Поскольку
Отсюда
- Поскольку
Отсюда
- Поскольку
Отсюда
Если длины отрезков на рисунке 173 обозначить так:
АС = Ь, 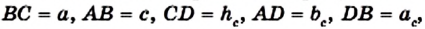
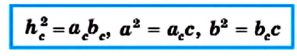
Эти равенства называют метрическими соотношениями в прямоугольном треугольнике.
Пример:
Даны два отрезка, длины которых равны а и b (рис. 174). Постройте третий отрезок, длина которого равна
Решение:
Рассмотрим треугольник ADC 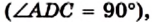
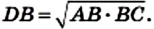
Проведенный анализ показывает, как провести построение.
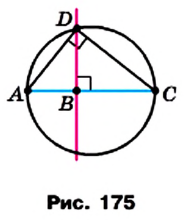
На произвольной прямой отметим точку А и отложим последовательно отрезки АВ и ВС так, чтобы АВ = а, ВС = b. Построим окружность с диаметром АС. Через точку В проведем прямую, перпендикулярную прямой АС (рис. 175).
Докажем, что отрезок DB искомый. Действительно, 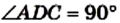
Видео:Метрические соотношения в прямоугольном треугольнике. 2 часть. 9 класс.Скачать

Теорема Пифагора
Теорема 16.1 (теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство. На рисунке 176 изображен прямоугольный треугольник ABC 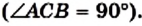
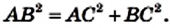
Проведем высоту CD. Применив теорему 15.1 для катетов АС и ВС, получаем:
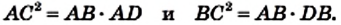
Далее имеем:
Если в прямоугольном треугольнике длины катетов равны а и b, а длина гипотенузы равна с, то теорему Пифагора можно выразить следующим равенством:
Теорема Пифагора позволяет по двум сторонам прямоугольного треугольника найти его третью сторону:
Из равенства 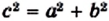
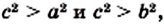
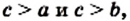
1 Другим способом этот факт был установлен в курсе геометрии 7 класса.
Пифагор:
Вы изучили знаменитую теорему, которая носит имя выдающегося древнегреческого ученого Пифагора.
Исследования древних текстов свидетельствуют о том, что утверждение этой теоремы было известно задолго до Пифагора. Почему же ее приписывают Пифагору? Скорее всего потому, что именно Пифагор нашел доказательство этого утверждения.
О жизни Пифагора мало что известно достоверно. Он родился на греческом острове Самос. По преданиям, он много путешествовал, приобретая знания и мудрость.
Поселившись в греческой колонии Кротон (на юге Италии), он окружил себя преданными учениками и единомышленниками. Так возник пифагорейский союз (или кротонское братство). Влияние этого союза было столь велико, что даже спустя столетия после смерти Пифагора многие выдающиеся математики Древнего мира Пифагор называли себя пифагорейцами.
Тригонометрические функции острого угла прямоугольного треугольника
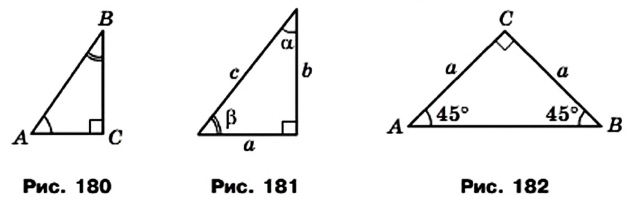
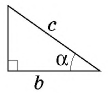
На рисунке 180 изображен прямоугольный треугольник АВС 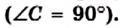
Определение. Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
Синус угла А обозначают так: sin А (читают: «синус А»). Для острых углов А и В прямоугольного треугольника АВС имеем: 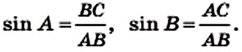
Для прямоугольного треугольника, изображенного на рисунке 181, можно записать:
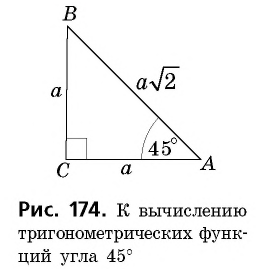
Рассмотрим прямоугольный равнобедренный треугольник АВС 
Имеем: 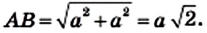
По определению 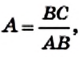
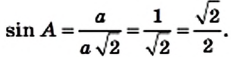
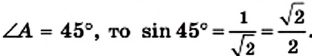
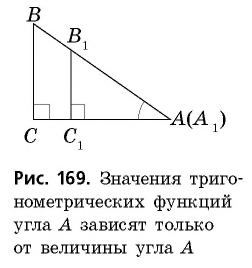
Вообще, если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны.
Действительно, эти прямоугольные треугольники подобны по первому признаку подобия треугольников. Поэтому отношение катета к гипотенузе одного треугольника равно отношению соответственного катета к гипотенузе другого треугольника.
Например, запись sin 17° можно отнести ко всем углам, градусные меры которых равны 17°. Значение этого синуса можно вычислить один раз, выбрав произвольный прямоугольный треугольник с острым углом 17°.
Следовательно, синус острого угла зависит только от величины этого угла.
Определение. Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
Косинус угла А обозначают так: cos А (читают: «косинус А»).
Для острых углов А и В прямоугольного треугольника АВС (рис. 180) можно записать:
Отметим, что катет прямоугольного треугольника меньше его гипотенузы, а поэтому синус и косинус острого угла меньше 1.
Определение. Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.
Тангенс угла А обозначают так: tg А (читают: «тангенс А»).
Для острых углов А и В прямоугольного треугольника АВС (рис. 180) можно записать:
Определение. Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему.
Котангенс угла А обозначают так: ctg А (читают: «котангенс А»). Для острых углов А и В прямоугольного треугольника АВС (рис. 180) можно записать: 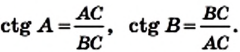
Для прямоугольного треугольника, изображенного на рисунке 181, записывают:
Как было установлено, синус угла зависит только от величины угла. Рассуждая аналогично, можно прийти к следующему выводу: косинус, тангенс и котангенс острого угла зависят только от величины этого угла.
Вообще, каждому острому углу а соответствует единственное число — значение синуса (косинуса, тангенса, котангенса) этого угла. Поэтому зависимость значения синуса (косинуса, тангенса, котангенса) острого угла от величины этого угла является функциональной. Функцию, соответствующую этой зависимости, называют тригонометрической. Так, 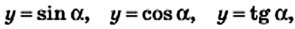
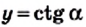
С древних времен люди составляли таблицы приближенных значений тригонометрических функции с некоторым шагом, один раз вычисляя значения тригонометрических функций для конкретного аргумента. Затем эти таблицы широко использовались во многих областях науки и техники.
В наше время значения тригонометрических функций острых углов удобно находить с помощью микрокалькулятора.
Тангенс и котангенс острого угла можно выразить через синус и косинус этого же угла. Рассмотрим прямоугольный треугольник (рис. 181).
Запишем: 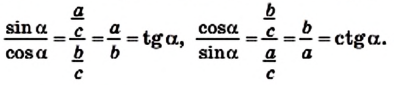
Заметим, что тангенс и котангенс одного и того же острого угла являются взаимно обратными числами, то есть имеет место равенство:
По теореме Пифагора 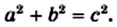
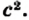
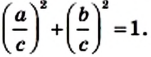
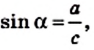
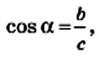
Принято записывать:
Отсюда имеем: 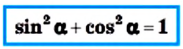
Эту формулу называют основным тригонометрическим тождеством.
Отметим, что 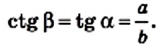

Мы уже знаем, что 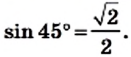
Имеем:
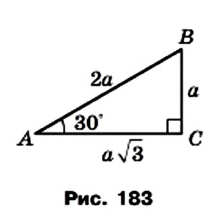
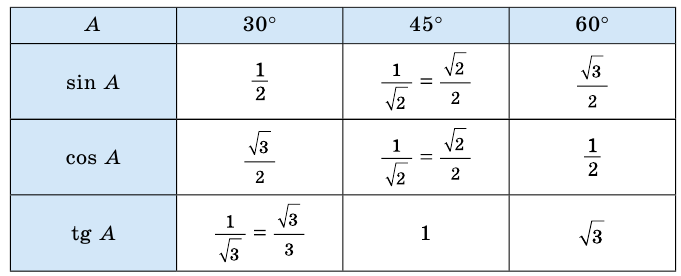
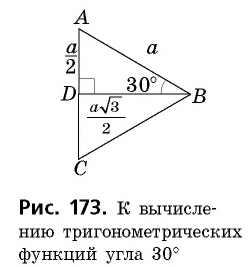
Найдем синус, косинус, тангенс и котангенс углов 30° и 60°. Рассмотрим прямоугольный треугольник АВС, в котором 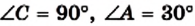
Пусть ВС = а. Тогда по свойству катета, лежащего против угла 30°, получаем, что АВ = 2а. Из теоремы Пифагора следует, что
Имеем: 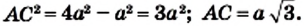
Отсюда находим:
Поскольку 60° = 90° — 30°, то получаем:
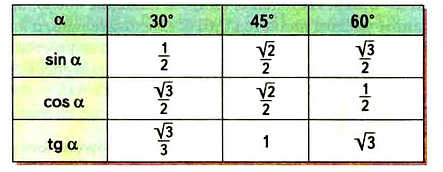
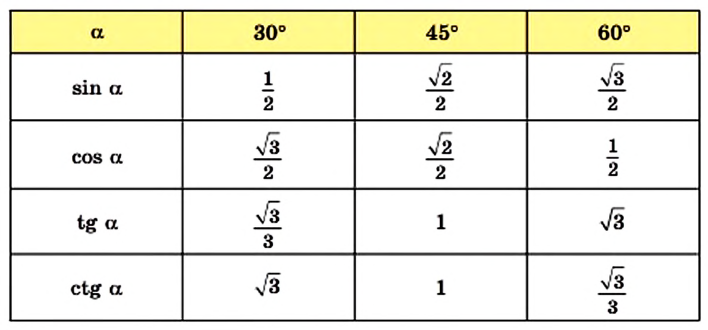
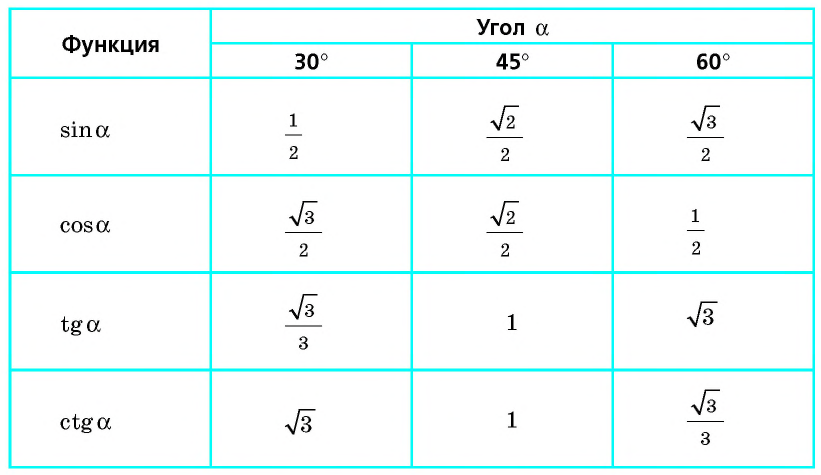
Значения синуса, косинуса, тангенса и котангенса для углов 30°, 45° и 60° полезно запомнить.
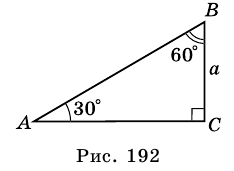
Решение прямоугольных треугольников
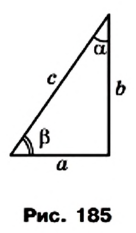
На рисунке 185 изображен прямоугольный треугольник с острыми углами 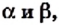
По определению синуса острого угла прямоугольного треугольника
Отсюда
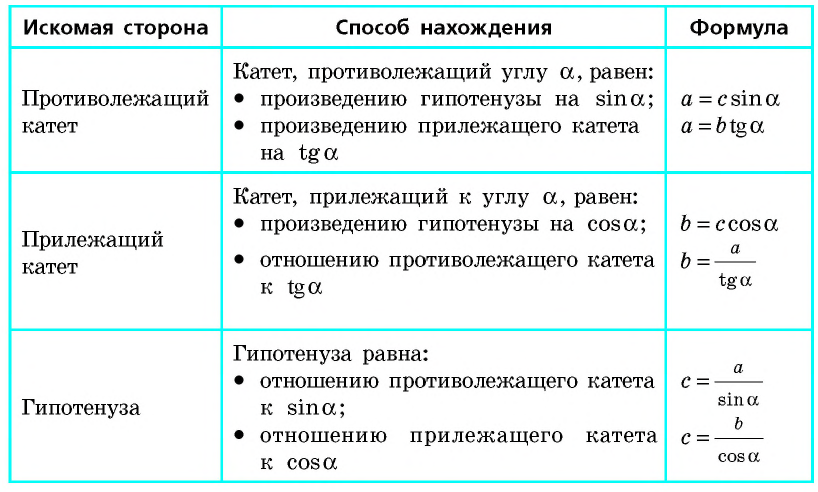
Следовательно, катет прямоугольного треугольника равен произведению гипотенузы на синус угла, противолежащего этому катету.
По определению косинуса острого угла прямоугольного треугольника 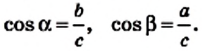
Следовательно, катет прямоугольного треугольника равен произведению гипотенузы на косинус угла, прилежащего к этому катету.
По определению тангенса острого угла прямоугольного треугольника 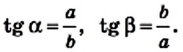
Следовательно, катет прямоугольного треугольника равен произведению второго катета на тангенс угла, противолежащего первому катету.
По определению котангенса острого угла прямоугольного треугольника 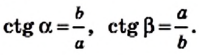
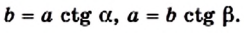
Следовательно, катет прямоугольного треугольника равен произведению второго катета на котангенс угла, прилежащего к первому катету.
Из равенств 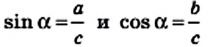
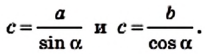
Следовательно, гипотенуза прямоугольного треугольника равна частному от деления катета на синус противолежащего ему угла;
- гипотенуза прямоугольного треугольника равна частному от деления катета на косинус прилежащего к нему угла.
Решить прямоугольный треугольник означает найти его стороны и углы по известным сторонам и углам.
Приведенные выше правила позволяют решать прямоугольный треугольник по одной стороне и одному острому углу.
В задачах на решение прямоугольных треугольников, если не обусловлено иначе, приняты такие обозначения (см. рис. 185): с — гипотенуза, а и b — катеты, 
Пример №1
Решите прямоугольный треугольник по катету и острому углу: a = 14 см, 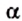
Решение:
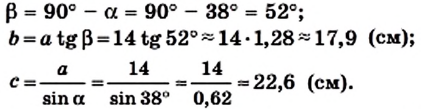
Ответ:
Отметим, что эту задачу можно было решить и другим способом: например, найти гипотенузу, используя теорему Пифагора.
Пример №2
Решите прямоугольный треугольник по катету и гипотенузе:
a = 26 см, с = 34 см.
Решение:
Имеем:
Вычисляем угол 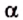
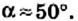
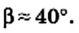
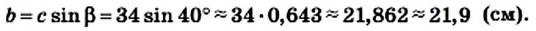
Ответ:
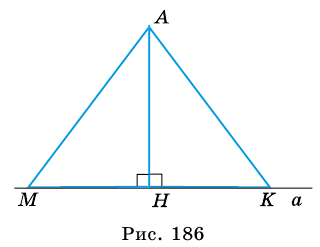
Пример №3
Высота AD треугольника АВС (рис. 186) делит его сторону ВС на отрезки BD и CD такие, что 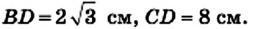
Решение:
Из треугольника 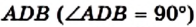
Из треугольника 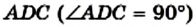
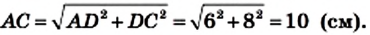
Ответ:
Пример №4
Боковая сторона равнобедренного треугольника равна b, угол при основании равен 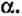
Решение:
В треугольнике АВС (рис. 187)
Проведем высоту BD.
Из треугольника 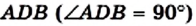
Точка О — центр окружности, вписанной в треугольник АВС. Следовательно, точка О принадлежит высоте ВD и биссектрисе АО угла ВАС. Поскольку 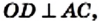
Из треугольника 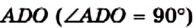
Ответ:
Напомню:
Метрические соотношения в прямоугольном треугольнике
- Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу.
- Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.
Теорема Пифагора
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Синус острого угла прямоугольного треугольника
- Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника
- Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника
- Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.
Котангенс острого угла прямоугольного треугольника
- Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему.
Тригонометрические формулы
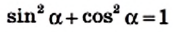
Соотношения между сторонами и значениями тригонометрических функций углов в прямоугольном треугольнике
- Катет прямоугольного треугольника равен произведению гипотенузы на синус угла, противолежащего этому катету.
- Катет прямоугольного треугольника равен произведению гипотенузы на косинус угла, прилежащего к этому катету.
- Катет прямоугольного треугольника равен произведению второго катета на тангенс угла, противолежащего первому катет>г.
- Катет прямоугольного треугольника равен произведению второго катета на котангенс угла, прилежащего к первому’ катету.
- Гипотенуза прямоугольного треугольника равна частному от деления катета на синус противолежащего ему угла.
- Гипотенуза прямоугольного треугольника равна частному от деления катета на косинус прилежащего к нему угла.
Четырехугольник, его элементы. Сумма углов четырехугольника
Рассмотрим одну из важнейших теорем геометрии, которая показывает зависимость между катетами и гипотенузой прямоугольного треугольника.
Теорема 1 (теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
На сегодняшний день известны более ста доказательств этой теоремы. Рассмотрим одно из них.
Доказательство:
Пусть 
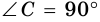
1) Проведем высоту 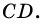
2) По теореме о средних пропорциональных отрезках в прямоугольном треугольнике имеем:
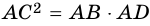
3) Сложим эти два равенства почленно. Учитывая, что 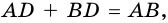
4) Следовательно,
Если в треугольнике 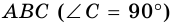
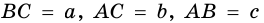
Таким образом, зная две стороны прямоугольного треугольника, с помощью теоремы Пифагора можно найти третью. В этом нам поможет следующая схема:
Пример №5
Катеты прямоугольного треугольника равны 7 см и 24 см. Найдите гипотенузу.
Решение:
Пусть 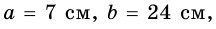
Пример №6
Гипотенуза прямоугольного треугольника равна 17 см, а один из катетов — 15 см. Найдите второй катет.
Решение:
Пусть 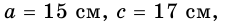
Пример №7
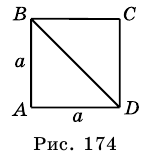
Найдите диагональ квадрата, сторона которого равна
Решение:
Рассмотрим квадрат 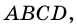
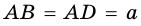
Ответ.
Пример №8
Найдите медиану равностороннего треугольника со стороной
Решение:
Рассмотрим равносторонний треугольник 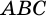
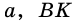
Так как 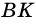
Из 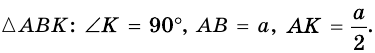
Ответ:
Пример №9
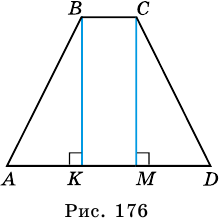
Основания равнобокой трапеции равны 12 см и 22 см, а боковая сторона — 13 см. Найдите высоту трапеции.
Решение:
Пусть 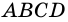
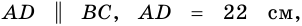
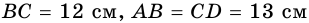
1) Проведем высоты 
2) 
3) Из 
Пример №10
Один из катетов прямоугольного треугольника равен 8 см, а второй на 2 см меньше гипотенузы. Найдите неизвестный катет треугольника.
Решение:
Пусть 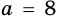
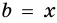
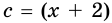
Так как по теореме Пифагора 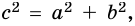
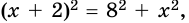
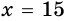
Следовательно, неизвестный катет равен 15 см.
Верно и утверждение, обратное теореме Пифагора.
Теорема 2 (обратная теореме Пифагора). Если для треугольника 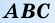
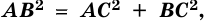
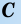
Доказательство:
Пусть в треугольнике 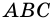
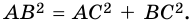
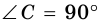
Рассмотрим 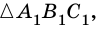
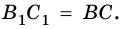
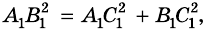
Но 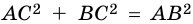
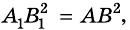
Таким образом, 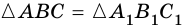
Так как 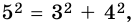
Тройку целых чисел, удовлетворяющую теореме Пифагора, называют пифагоровой тройкой чисел, а треугольник, стороны которого равны этим числам, — пифагоровым треугольником. Например, пифагоровой является не только тройка чисел 3, 4, 5, но и 7, 24, 25 или 9, 40, 41 и т. п.
Заметим, что из теоремы Пифагора и теоремы, ей обратной, следует, что
треугольник является прямоугольным тогда и только тогда, когда квадрат наибольшей стороны треугольника равен сумме квадратов двух других его сторон.
Пример №11
Является ли прямоугольным треугольник со сторонами: 1) 6; 8; 10; 2) 5; 7; 9?
Решение:
1) Так как 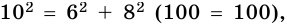
2) Так как 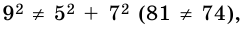
Ответ. 1) Да; 2) нет.
Теорема, названная в честь древнегреческого философа и математика Пифагора, была известна задолго до него. В текстах давних вавилонян о ней вспоминалось еще за 1200 лет до Пифагора. Скорее всего, доказывать эту теорему вавилоняне не умели, а зависимость между катетами и гипотенузой прямоугольного треугольника установили опытным путем. Также эта теорема была известна в Древнем Египте и Китае.
Считается, что Пифагор — первый, кто предложил строгое доказательство теоремы. Он сформулировал теорему так: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах». Именно в такой формулировке она и была доказана Пифагором.
Рисунок к этому доказательству еще называют «пифагоровыми штанами».
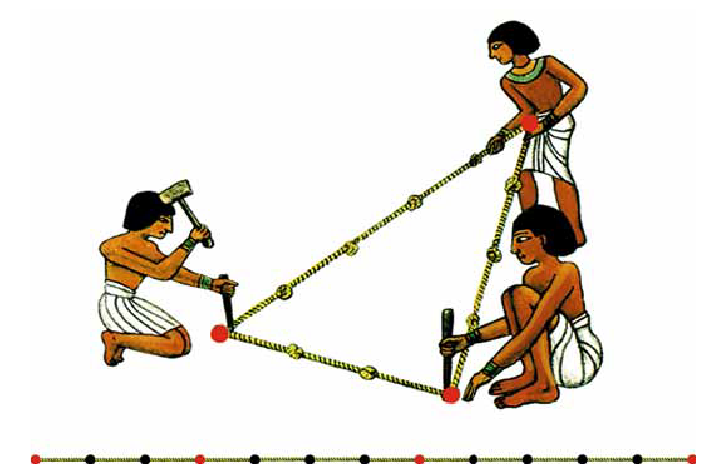
Зная, что треугольник со сторонами 3, 4 и 5 является прямоугольным, землемеры Древнего Египта использовали его для построения прямого угла. Бечевку делили узлами на 12 равных частей и соединяли ее концы. Потом веревку растягивали и с помощью колышков фиксировали на земле в виде треугольника со сторонами 3; 4; 5. В результате угол, противолежащий стороне, длина которой 5, был прямым.
Перпендикуляр и наклонная, их свойства
Пусть 
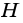
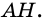
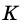
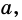
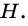
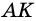
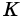
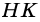
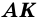
Рассмотрим свойства перпендикуляра и наклонной.
1. Перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из этой точки к этой прямой.
Действительно, в прямоугольном треугольнике 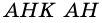
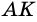
2. Если две наклонные, проведенные к прямой из одной точки, равны, то равны и их проекции.
Пусть из точки 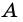
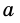
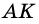
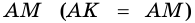
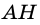
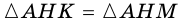
Верно и обратное утверждение.
3. Если проекции двух наклонных, проведенных из точки к прямой, равны, то равны и сами наклонные.
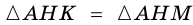
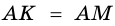
4. Из двух наклонных, проведенных из точки к прямой, большей является та, у которой больше проекция.
Пусть 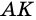
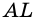
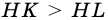
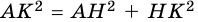
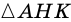
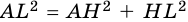
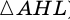
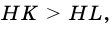
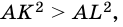
Свойство справедливо и в случае, когда точки 
Верно и обратное утверждение.
5. Из двух наклонных, проведенных из точки к прямой, большая наклонная имеет большую проекцию.
Пусть 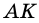
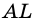
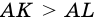
Тогда 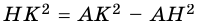
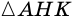
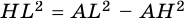
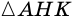
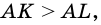
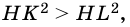
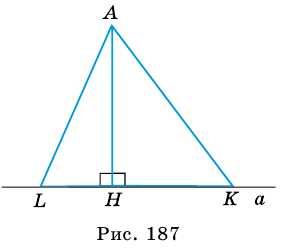
Пример №12
Из точки к прямой проведены две наклонные. Длина одной из них равна 10 см, а ее проекции — 6 см. Найдите длину второй наклонной, если она образует с прямой угол 30°.
Решение:
Пусть на рисунке 187 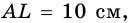
1) Из 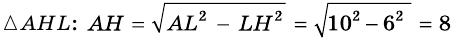
2) Из 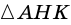
будем иметь:
Поэтому
Ответ. 16 см.
Пример №13
Из точки 
Решение:
Пусть на рисунке 187 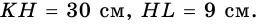
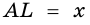
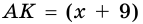
Из 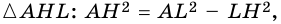
Из 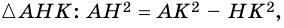
Левые части полученных равенств равны, следовательно, равны и правые их части.
Имеем уравнение: 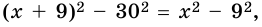
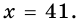
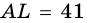
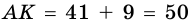
Ответ. 41 см, 50 см.
Синус, косинус и тангенс острого угла прямоугольного треугольника. Соотношения между сторонами и углами в прямоугольном треугольнике
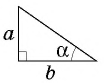
Рассмотрим прямоугольный треугольник 
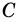
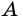
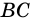
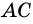
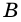
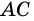
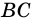
Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
Синус угла 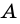
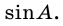
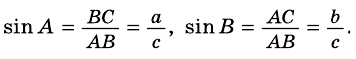
Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
Косинус угла 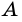
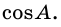
Так как катеты 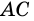
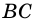
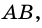
Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.
Тангенс угла 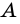
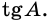
Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
Рассмотрим прямоугольные треугольники 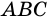
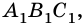
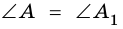
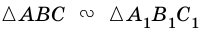
Из этого следует, что 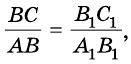
Аналогично 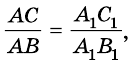
поэтому
Таким образом, приходим к выводу: синус, косинус и тангенс острого угла прямоугольного треугольника зависят только от градусной меры угла.
Из определений синуса, косинуса и тангенса угла получаем следующие соотношения между сторонами и углами в прямоугольном треугольнике.
1. Катет равен гипотенузе, умноженной на синус противолежащего ему угла или на косинус прилежащего: 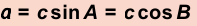
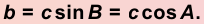
2. Гипотенуза равна катету, деленному на синус противолежащего ему угла или на косинус прилежащего:
3. Катет, противолежащий углу 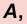
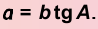
4. Катет, прилежащий к углу 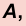
Значения 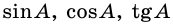

Пример №14
В треугольнике 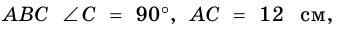
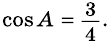
Решение:
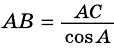
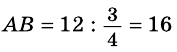
Пример №15
В треугольнике 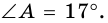
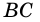
Решение:
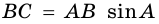
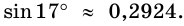
Ответ. 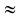
С помощью таблиц, калькулятора или компьютера можно по данному значению 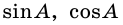
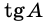
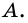

Пример №16
В треугольнике 
Найдите острые углы треугольника.
Решение:
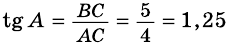
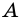
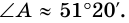
Ответ.
Найдем синус, косинус и тангенс углов 30° и 60°. Рассмотрим 
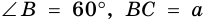
Тогда по свойству катета, противолежащего углу 30°,
По теореме Пифагора:
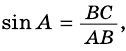
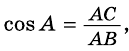
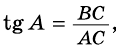
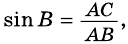
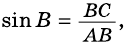
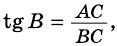
Найдем синус, косинус и тангенс угла 45°.
Рассмотрим 
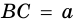
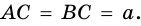
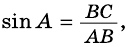
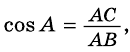
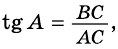
Систематизируем полученные данные в таблицу:
Пример №17
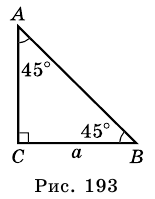
Найдите высоту равнобедренного треугольника, проведенную к основанию, если основание равно 12 см, а угол при вершине треугольника равен 120°.
Решение:
Пусть 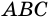
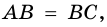
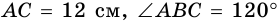
Проведем к основанию 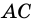
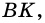
Из
отсюда 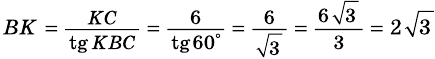
Ответ. 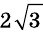
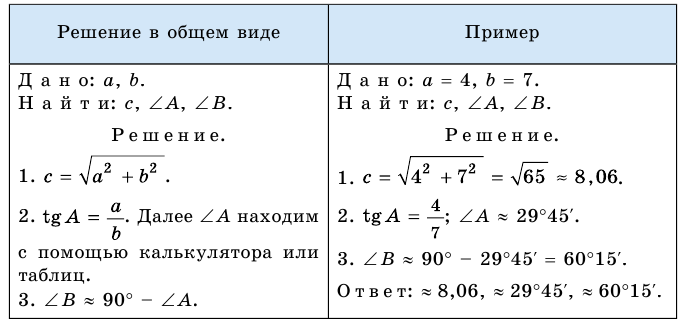
Вычисление прямоугольных треугольников
Решить треугольник — значит найти все неизвестные его стороны и углы по известным сторонам и углам.
Для того чтобы можно было решить прямоугольный треугольник, известными должны быть или две стороны треугольника или одна из сторон и один из острых углов треугольника.
Используя в прямоугольном треугольнике 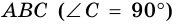
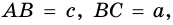
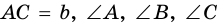
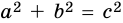
можно решить любой прямоугольный треугольник.
Рассмотрим четыре вида задач на решение прямоугольных треугольников.
Образцы записи их решения в общем виде и примеры задач представлены в виде таблиц.
Решение прямоугольных треугольников по гипотенузе и острому углу
Пример:
Дано гипотенузу 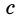
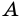
Решение прямоугольных треугольников по катету и острому углу
Пример:
Дано катет 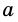
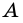
Решение прямоугольных треугольников по двум катетам
Пример:
Дано катеты 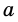
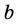
Решение прямоугольных треугольников по катету и гипотенузе
Пример:
Дано катет 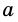
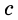
Пример:
Найдите высоту дерева 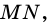
Решение:
Обозначим на прямой, проходящей через точку 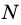
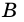
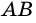
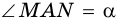
1) В
2) В
3) Так как 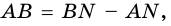
откуда
Ответ.
Видео:Метрические соотношения в треугольнике. ГеометрияСкачать

Определение прямоугольных треугольников
Из этой главы вы узнаете, как решать прямоугольные треугольники, т. е. находить их неизвестные стороны и углы по известным. Необходимые для этого теоретические знания можно почерпнуть из раздела математики, родственного как с геометрией, так и с алгеброй, — из тригонометрии. Собственно, само слово «тригонометрия» в переводе с греческого означает «измерение треугольников». Поэтому отношения сторон прямоугольного треугольника, с которыми вы познакомитесь далее, получили название тригонометрических функций.
Соотношения, которые будут применяться в этой главе, в полной мере можно считать проявлением подобия треугольников. Вообще, подобие треугольников, теорема Пифагора и площадь — это те три кита, на которых держится геометрия многоугольника. Именно исследование взаимосвязей между этими теоретическими фактами и составляет основное содержание курса геометрии в восьмом классе.
Синус, косинус и тангенс
Как уже было доказано, все прямоугольные треугольники, имеющие по равному острому углу, подобны. Свойство подобия обусловливает не только равенство отношений пропорциональных сторон этих треугольников, но и равенство отношений между катетами и гипотенузой каждого из этих треугольников. Именно эти отношения и будут предметом дальнейшего рассмотрения.
Пусть дан прямоугольный треугольник с катетами 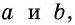
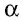
Определение
Синусом острого угла 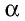
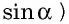
Косинусом острого угла 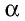
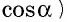
Тангенсом острого угла 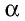
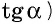
Кроме синуса, косинуса и тангенса, рассматривают также котангенс острого угла 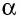
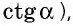
Поскольку катет прямоугольного треугольника меньше гипотенузы, то синус и косинус острого угла меньше единицы.
Покажем, что значения тригонометрических функций зависят только от величины угла. Пусть прямоугольные треугольники 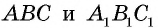
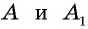
Эти треугольники подобны, отсюда 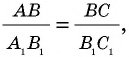
Правая и левая части этого равенства по определению равны синусам острых углов 
т.е. синус угла 
Имеет место еще один важный факт: если значения некоторой тригонометрической функции для острых углов 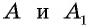
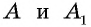
Пример №18
Найдите синус, косинус и тангенс наименьшего угла египетского треугольника.
Решение:
Пусть в треугольнике 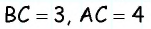
Поскольку в треугольнике наименьший угол лежит против наименьшей стороны, то угол 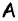
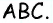
Ответ:
Тригонометрические тождества
Выведем соотношения (тождества), которые выражают зависимость между тригонометрическими функциями одного угла.
Теорема (основное тригонометрическое тождество)
Для любого острого угла
По определению синуса и косинуса острого угла прямоугольного треугольника (см. рис. 168) имеем:
По теореме Пифагора числитель этой дроби равен
Следствие
Для любого острого угла
Докажем еще несколько тригонометрических тождеств.
Непосредственно из определений синуса
sin a а b ас а и косинуса имеем: 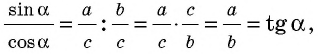
Аналогично доказывается, что
Отсюда следует, что
Пример №19
Найдите косинус и тангенс острого угла прямоугольного треугольника, синус которого равен 0,8.
Решение:
Пусть для острого угла 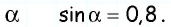
Поскольку
Ответ:
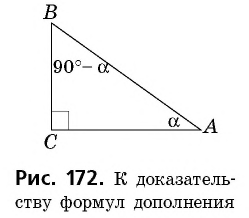
Вычисление значений тригонометрических функций. Формулы дополнения
Тригонометрические тождества, которые мы рассмотрели, устанавливают взаимосвязь между разными тригонометрическими функциями одного угла. Попробуем установить связь между функциями двух острых углов прямоугольного треугольника.
Теорема (формулы дополнения)
Для любого острого угла
Рассмотрим прямоугольный треугольник 
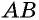
Если 
Следствие
Для любого острого угла
Заметим, что название «формулы дополнения», как и название «косинус», в котором префикс «ко» означает «дополнительный», объясняется тем, что косинус является синусом угла, который дополняет данный угол до 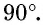
Значения тригонометрических функций углов 30 45 60
Вычислим значения тригонометрических функций угла 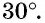
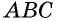
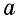
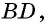
В треугольнике 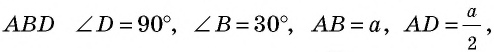
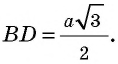
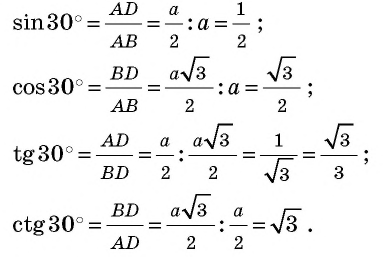
С помощью формул дополнения получаем значения тригонометрических функций угла
Для вычисления значений тригонометрических функций угла 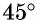
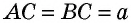
По теореме Пифагора 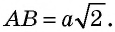
Представим значения тригонометрических функций углов 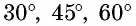
Значения тригонометрических функций других углов можно вычислить с помощью калькулятора или специальных таблиц (см. Приложение 3).
Решение прямоугольных треугольников
Нахождение неизвестных сторон прямоугольного треугольника
Пусть дан прямоугольный треугольник с катетами 
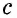
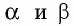
Зная градусную меру угла 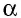
Заметим, что для нахождения неизвестных сторон прямоугольного треугольника можно использовать и 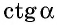
Запоминать содержание справочной таблицы не обязательно. Для нахождения неизвестной стороны прямоугольного треугольника можно действовать по такому плану.
1. Выбрать формулу определения той тригонометрической функции данного угла, которая связывает искомую сторону с известной (этот этап можно выполнить устно).
2. Выразить из этой формулы искомую сторону.
3. Провести необходимые вычисления.
Пример №20
В прямоугольном треугольнике с гипотенузой 12 м найдите катет, прилежащий к углу
Решение:
Пусть в прямоугольном треугольнике (см. рисунок) 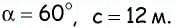
Поскольку
Ответ: 6 м.
Примеры решения прямоугольных треугольников
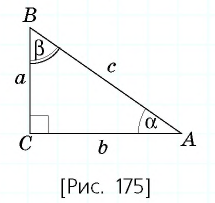
Решить треугольник означает найти его неизвестные стороны и углы по известным сторонам и углам. Прямоугольный треугольник можно решить по стороне и острому углу или по двум сторонам. Рассмотрим примеры конкретных задач на решение прямоугольных треугольников, пользуясь обозначениями рисунка 175. При этом договоримся округлять значения тригонометрических функций до тысячных, длины сторон — до сотых, а градусные меры углов — до единиц.
Пример №21
Решите прямоугольный треугольник по гипотенузе 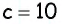
Решение:
Поскольку сумма острых углов прямоугольного треугольника равна
Поскольку
т.е.
Поскольку
т.е.
Пример №22
Решите прямоугольный треугольник по катету 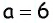
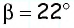
Решение:
Поскольку сумма острых углов прямоугольного треугольника равна
Поскольку
Поскольку
Пример №23
Решите прямоугольный треугольник по гипотенузе 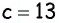
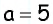
Решение:
По теореме Пифагора
Поскольку 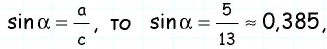
Поскольку сумма острых углов прямоугольного треугольника равна
Пример №24
Решите прямоугольный треугольник по катетам 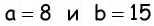
Решение:
По теореме Пифагора
Поскольку 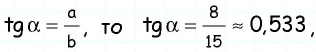
Поскольку сумма острых углов прямоугольного треугольника равна
На отдельных этапах решения задач 1—4 можно использовать другие способы. Но следует заметить, что в том случае, когда одна из двух сторон треугольника найдена приближенно, для более точного нахождения третьей стороны целесообразно использовать определения тригонометрических функций.
Рассмотрим примеры применения решения треугольников в практических задачах.
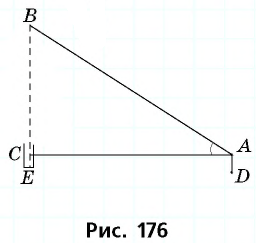
Пример №25
Найдите высоту данного предмета (рис. 176).
Решение:
На определенном расстоянии от данного предмета выберем точку 
Поскольку в прямоугольном треугольнике
Для определения высоты предмета необходимо прибавить к 

Пример №26
Насыпь шоссейной дороги имеет ширину 60 м в верхней части и 68 м в нижней. Найдите высоту насыпи, если углы наклона откосов к горизонту равны
Решение:
Рассмотрим равнобедренную трапецию 
Проведем высоты 
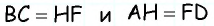
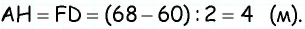
Поскольку
т.е.
Ответ:
Синусом острого угла 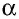
Косинусом острого угла 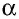
Тангенсом острого угла 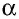
Котангенсом острого угла 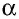
Тригонометрические тождества
Значения тригонометрических функций некоторых углов
Видео:8 класс Геометрия. Метрические соотношения в прямоугольном треугольнике. Высота к гипотенузе Урок #7Скачать

Историческая справка
Умение решать треугольники необходимо при рассмотрении многих практических задач, возникающих в связи с потребностями географии, астрономии, навигации. Поэтому элементы тригонометрии появились еще в Древнем Вавилоне в период интенсивного развития астрономии. В работе греческого ученого Птолемея «Альмагест» (II в. н. где изложена античная система мира, содержатся элементы сферической тригонометрии.
В Древней Греции вместо синуса угла 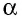
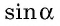
Синус и косинус как вспомогательные величины использовались индийскими математиками в V в., а тангенс и котангенс впервые появились в работах арабского математика X в. Абу-аль-Вефы.
Как отдельный раздел математики тригонометрия выделилась в произведениях персидского ученого Насреддина Туси (1201-1274), а системное изложение тригонометрии первым из европейцев представил немецкий математик и механик Иоганн Мюллер (1436-1476), более известный под псевдонимом Региомонтан.
Современную форму изложения и современную символику тригонометрия приобрела благодаря Леонарду Эйлеру в XVIII в. Кроме известных вам четырех тригонометрических функций иногда рассматриваются еще две:
секанс
и косеканс
Приложения
Обобщенная теорема Фалеса и площадь прямоугольника
В ходе доказательства некоторых геометрических теорем используется процедура деления отрезка на некоторое количество равных частей. Это позволяет дать числовые оценки в виде неравенств и с их помощью получить противоречие.
В курсе геометрии 8 класса такой подход целесообразно применить для доказательства двух приведенных ниже теорем.
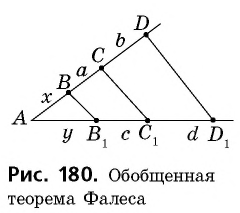
Теорема (обобщенная теорема Фалеса)
Параллельные прямые, пересекающие стороны угла, отсекают на сторонах этого угла пропорциональные отрезки.
По данным рисунка 180 докажем три формулы:
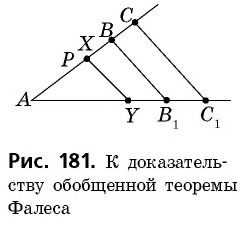
Докажем сначала формулу 1. Пусть отрезок 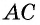
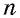
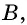
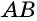
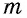
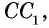
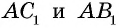
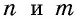
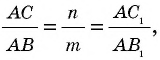
Если описанное деление отрезка 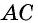
Рассмотрим случай, когда 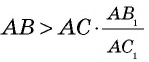
Отложим на отрезке 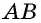
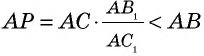
Разобьем отрезок 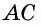
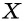
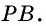
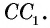
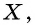
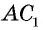
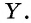
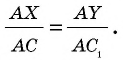
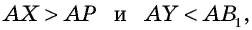
Это неравенство противоречит выбору длины отрезка 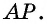
Докажем формулы 2 и 3. Пользуясь обозначениями рисунка 180,
по формуле 1 имеем 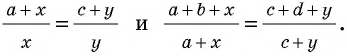
Откуда 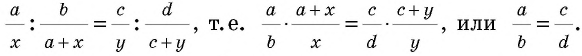
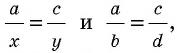
Теорема доказана полностью.
Из курса математики 5 класса известно, что площадь прямоугольника равна произведению двух его соседних сторон. Так, на рисунке 182 дан прямоугольник 
Таким способом легко найти площадь прямоугольника, у которого длины сторон выражены любыми целыми числами. Но справедливость этой формулы при условии, что длины сторон прямоугольника не являются целыми числами,— совсем неочевидная теорема. Докажем ее.
Теорема (формула площади прямоугольника)
Площадь прямоугольника равна произведению его соседних сторон:
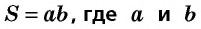
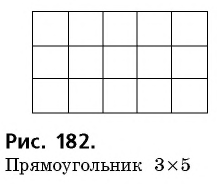
Докажем сначала, что площади прямоугольников с одним равным измерением относятся как длины других измерений.
Пусть прямоугольники 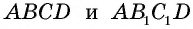
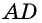
Разобьем сторону 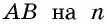
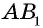
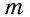
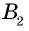
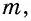
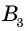
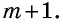
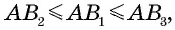
Теперь проведем через точки деления прямые, параллельные 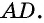
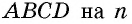
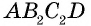
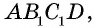
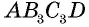
Следовательно,
Имеем:
Сравнивая выражения для 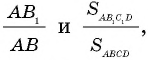
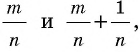
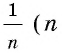
Действительно, если это не так, т.е. 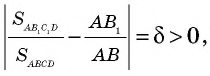
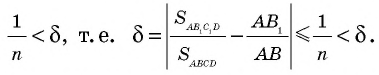
Рассмотрим теперь прямоугольники 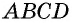
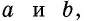
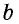
Тогда по доказанному
Поскольку 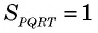
Золотое сечение
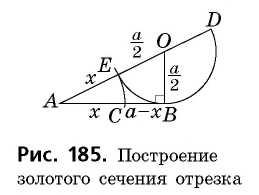
С давних времен люди старались познать мир путем поиска гармонии и совершенства. Одним из вопросов, которыми задавались еще древние греки, был поиск наилучшего соотношения неравных частей одного целого. Таким соотношением еще со времен Пифагора считали гармоническое деление, при котором меньшая часть относится к большей, как большая часть относится ко всему целому. Такое деление отрезка на части описано во II книге «Начал» Евклида и названо делением в среднем и крайнем отношении. Рассмотрим деление отрезка 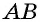
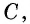
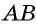
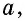
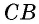
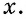
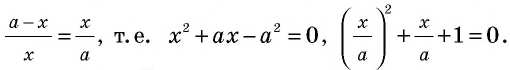
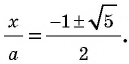
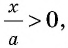
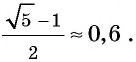
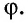
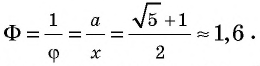
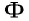
В эпоху Возрождения (XV—XVII вв.) интерес к гармоническому делению чрезвычайно возрос. Выдающийся ученый и художник Леонардо да Винчи (1452—1519) назвал такое деление золотым сечением, а его современник и соотечественник, итальянский монах-математик Лука Па-чоли (1445—1514) — божественной пропорцией. Золотое сечение и близкие к нему пропорциональные отношения составляли основу композиционного построения многих произведений мирового искусства, в частности архитектуры Античности и Возрождения. Одно из величайших сооружений Древней Эллады — Парфенон в Афинах (V в. до н. э.) — содержит в себе золотые пропорции (в частности, отношение высоты к длине этого сооружения равно
Итак, дадим определение золотому сечению.
Определение:
Золотым сечением называется такое деление величины на две неравные части, при котором меньшая часть относится к большей, как большая часть относится ко всему целому.
Иначе говоря, золотое сечение — это деление величины в отношении 
Построить золотое сечение отрезка заданной длины 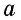
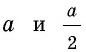
По теореме о пропорциональности отрезков секущей и касательной 
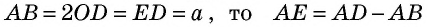
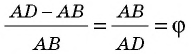
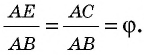
С золотым сечением связывают геометрические фигуры, при построении которых используются отношения 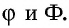
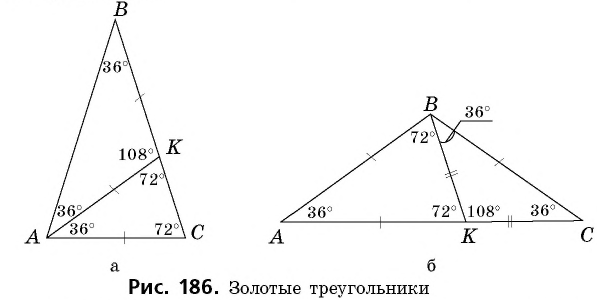
Равнобедренный треугольник называется золотым, если две его стороны относятся в золотом сечении. Докажем, что треугольник с углами 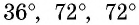
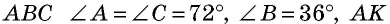
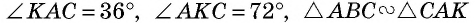
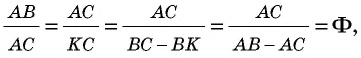
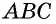
И наоборот: если в равнобедренном треугольнике 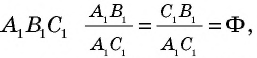
Предлагаем самостоятельно убедиться в том, что золотым является также треугольник с углами 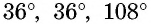
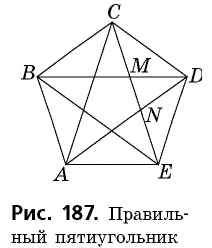
Золотые треугольники связаны с правильным пятиугольником (т.е. выпуклым пятиугольником, у которого все стороны равны и все углы равны).
В правильном пятиугольнике:
1) диагональ относится к стороне в золотом сечении;
2) точка пересечения диагоналей делит каждую из них в золотом сечении;
3) диагональ делит другую диагональ на два отрезка, один из которых делится в золотом сечении еще одной диагональю.
Согласно обозначениям рисунка 187 это означает, что 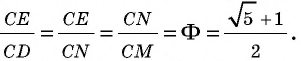
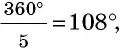
Диагонали правильного пятиугольника образуют звезду, которая в древние времена олицетворяла совершенство и имела мистическое значение. Пифагорейцы называли ее пентаграммой и избрали символом своей научной школы. В наши дни пятиконечная звезда — самая распространенная геометрическая фигура на флагах и гербах многих стран (приведите соответствующие примеры из истории и географии).
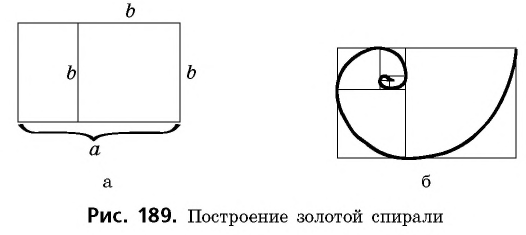
Прямоугольник называется золотым, если его стороны относятся в золотом сечении. Для построения золотого прямоугольника произвольный квадрат перегибаем пополам (рис. 188, а), проводим диагональ одного из полученных прямоугольников (рис. 188, б) и радиусом, равным этой диагонали, проводим дугу окружности с центром 
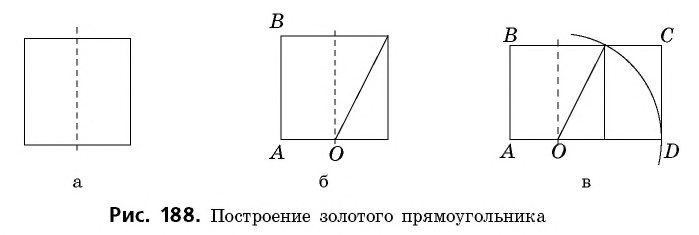
Если от золотого прямоугольника отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то оставшийся прямоугольник также будет золотым. Действительно, на рисунке 189, а имеем 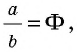
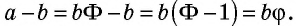
Через противолежащие вершины квадратов проходит так называемая золотая спираль, которая часто встречается в природе. Например, по принципу золотой спирали располагаются семена в подсолнечнике; по золотой спирали закручены раковины улиток, рога архаров, паутина отдельных видов пауков и даже наша Солнечная система, как и некоторые другие галактики.
Отметим также, что золотое сечение имеет немало алгебраических свойств. Отношение 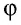
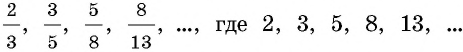
Золотое сечение, золотые многоугольники и золотая спираль являются математическими воплощениями идеальных пропорций в природе. Недаром великий немецкий поэт Иоганн Вольфганг Гете считал их математическими символами жизни и духовного развития.
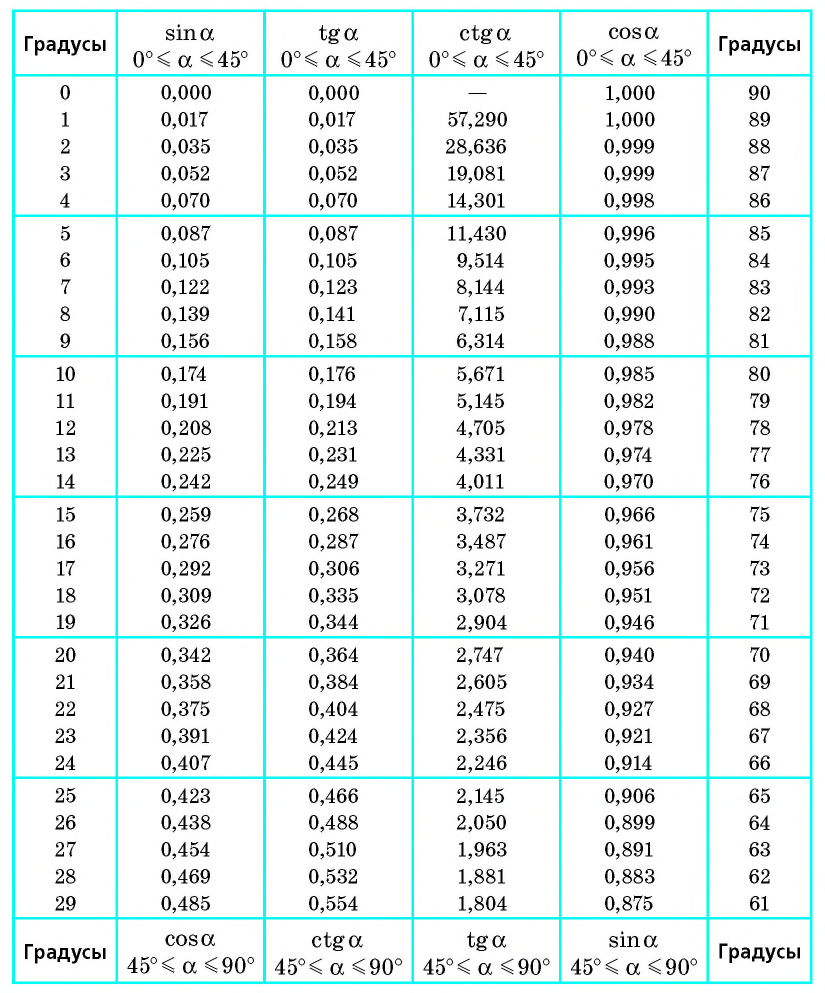
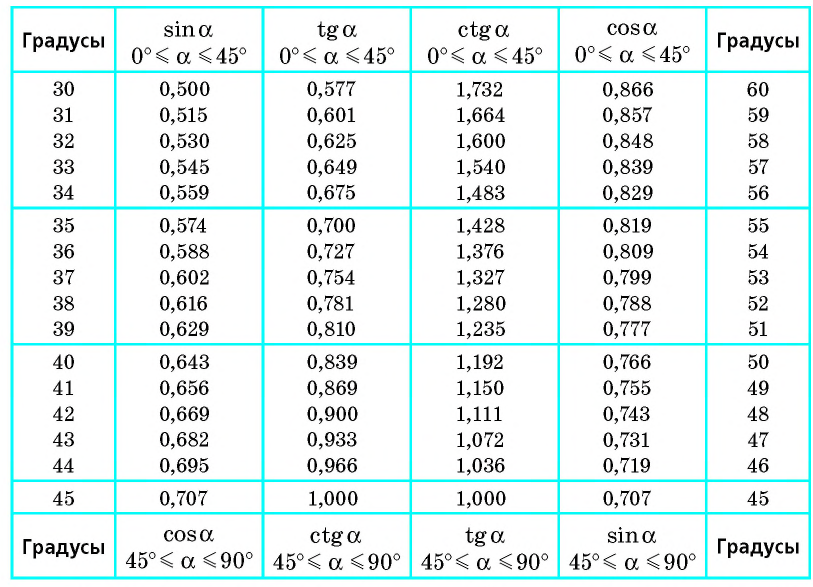
Приложение 3. Таблица значений тригонометрических функций
Значение тригонометрических функций острых углов можно приближенно определять с помощью специальных таблиц. Одна из таких таблиц представлена выше.
Таблица составлена с учетом формул дополнения. В двух крайних столбцах указаны градусные меры углов (в левом — от 
1-й — синусы углов от 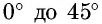
2-й — тангенсы углов от 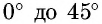
3-й — котангенсы углов от 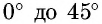
4-й — косинусы углов от 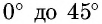
Рассмотрим несколько примеров применения данной таблицы. 1) Определим 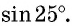
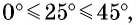
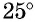
2) Определим 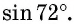
Доказать:
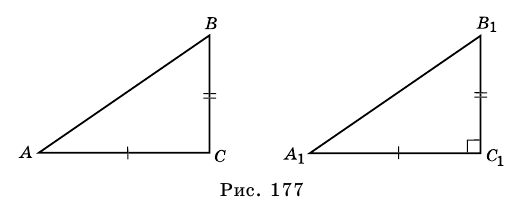
Доказательство. Проведём из вершины прямого угла С высоту CD. Каждый катет прямоугольного треугольника является средним пропорциональным между гипотенузой и его проекцией на гипотенузу. Поэтому 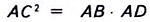
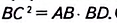
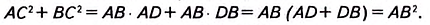
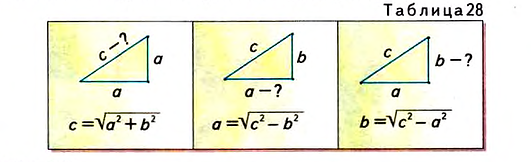
Если а и b — катеты прямоугольного треугольника, с — его гипотенуза, то из формулы 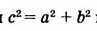
Используя эти формулы, по двум любым сторонам прямоугольного треугольника находим его третью сторону (табл. 28).
Справедлива и теорема, обратная теореме Пифагора: если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то этот треугольник — прямоугольный.
Согласно теореме, обратной теореме Пифагора, треугольник со сторонами 3 см, 4 см и 5 см — прямоугольный, поскольку 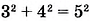
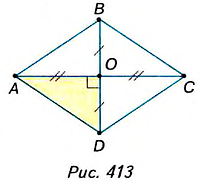
Пример №27
Сторона ромба равна 10 см, а одна из его диагоналей — 16 см. Найдите другую диагональ ромба.
Решение:
Пусть ABCD— ромб (рис. 413), АС= 16см,AD = 10см. Найдём диагональ BD. Как известно, диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам. Поэтому ∆AOD — прямоугольный ( ے 0= 90°). АС 16
В нём: катет 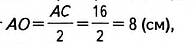
Для того чтобы найти определённый элемент фигуры (сторону, высоту, диагональ), выделите на рисунке прямоугольный треугольник, воспользовавшись свойствами фигуры, и примените теорему Пифагора.
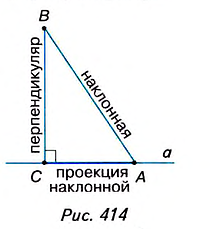
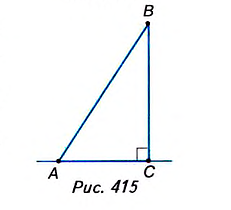
Пусть ВС — перпендикуляр, проведённый из точки В на прямую а (рис. 414). Возьмём произвольную точку А на прямой а, отличную от точки С, и соединим точки А и В. Отрезок АВ называется наклонной, проведённой из точки В на прямую а. Точка А называется основанием наклонной, а отрезок АС — проекцией наклонной.
Наклонные имеют следующие свойства. Если из данной точки к прямой провести перпендикуляр и наклонные, то:
- любая наклонная больше перпендикуляра;
- равные наклонные имеют равные проекции;
- из двух наклонных больше та, проекция которой больше.
Покажем, что свойства наклонных следуют из теоремы Пифагора.
- По теореме Пифагора,
(рис. 415), тогда
или АВ > ВС.
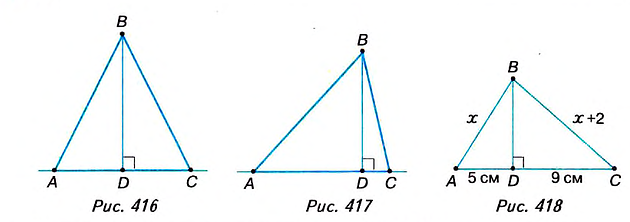
- Из прямоугольных треугольников ABD и CBD (рис. 416) имеем:
Поскольку в этих равенствах АВ = ВС (по условию), то AD = DC.
- Из прямоугольных треугольников ABD и CBD (рис. 417) имеем:
. В этих равенствах AD > DC. Тогда АВ > ВС.
Пример №28
Из точки к прямой проведены две наклонные, проекции которых равны 5 см и 9 см. Найдите наклонные, если одна из них на 2 см больше другой.
Решение:
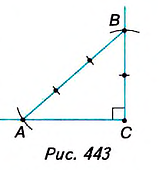
Пусть AD = 5 см, DC = 9 см (рис. 418). Поскольку AD ے A = a (рис. 441). Вы знаете, что катет а — противолежащий углу а, катет b — прилежащий к углу a . Отношение каждого катета к гипотенузе, а также катета к катету имеют специальные обозначения:
- — отношение
обозначают sin а и читают «синус альфа»;
- — отношение
обозначают cos а и читают «косинус альфа»;
- — отношение
обозначают tg а и читают «тангенс альфа».
Сформулируем определения sin a, cos а и tg а.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Отношение сторон прямоугольного треугольника и их обозначения указаны в
Зависят ли синус, косинус и тангенс острого угла от размеров треугольника?
Нет, не зависят. Итак, пусть ABC и 
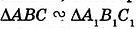
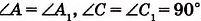
Из этих равенств следует:
Следовательно, в прямоугольных треугольниках с одним и тем же острым углом синусы этого утла равны, косинусы и тангенсы — равны. Если градусную меру угла изменить, то изменится и соотношение сторон прямоугольного треугольника. Это означает, что синус, косинус и тангенс острого угла прямоугольного треугольника зависят только от градусной меры угла и не зависят от размеров треугольника.
По исходному значению sin A, cos А или tg А можно построить угол А.
Пример №29
Постройте угол, синус которого равен 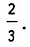
Решение:
Выбираем некоторый единичный отрезок (1 мм, 1 см, 1 дм). Строим прямоугольный треугольник, катет ВС которого равен двум единичным отрезкам, а гипотенуза АВ — трём (рис. 443). Угол А, лежащий против катета ВС, — искомый, поскольку sin А =
В прямоугольном треугольнике любой из двух катетов меньше гипотенузы. Поэтому sin а ے C = а (рис. 452). Проведём высоту BD. В прямоугольном треугольнике DBCкатет DC, прилежащий к углу а, равен произведению гипотенузы а на cos a: DC = a cos а. Поскольку высота равнобедренного треугольника, опущенная на основание, является медианой, то DC = AD. Тогда основание АС = 2 DC =2 a cos а.
В этой главе вы ознакомились с новыми приёмами вычисления длин сторон и градусных мер углов прямоугольного треугольника. Может возникнуть вопрос: Какова необходимость использования этих приёмов? Вы знаете, что в древности расстояния и углы сначала измеряли непосредственно инструментами. Например, транспортиром пользовались вавилоняне ещё за 2 ООО лет до н. э.
Но на практике непосредственно измерять расстояния и углы не всегда возможно. Как вычислить расстояние между двумя пунктами, которые разделяет препятствие (река, озеро, лес), расстояние до Солнца, Луны, как измерить высоту дерева, горы, как найти угол подъёма дороги либо угол при спуске с горы? Поэтому были открыты приёмы опосредствованного измерения расстояний и углов. При этом использовали равные либо подобные треугольники и геометрические построения. Строили на местности вспомогательный треугольник и измеряли необходимые его элементы.
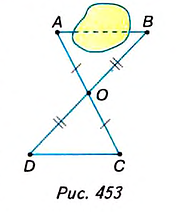
Итак, вы знаете, как определить расстояние между пунктами А и В, разделёнными препятствием (рис. 453). Для этого строим ∆COD = ∆АОВ и вместо искомого расстояния Ив измеряем равное ему расстояние CD.
Но при использовании этих приёмов получали недостаточно точные результаты, особенно при измерении значительных расстояний на местности. Кроме того, без угломерных инструментов нельзя найти градусные меры углов по длинам тех или других отрезков. Поэтому возникла необходимость в таких приёмах, когда непосредственные измерения сводились к минимуму, а результаты получали преимущественно вычислением элементов прямоугольного треугольника. В основе таких приёмов лежит использование cos а, sin а и tg а. Накопление вычислительных приёмов решения задач обусловило создание нового раздела математики, который в XVI в. назвали тригонометрией. Слово «тригонометрия» происходит от греческих слов trigonon — треугольник и metreo — измеряю. Греческих математиков Гиппарха (II в. до н. э.) и Птолемея (II в.) считают первыми, кто использовал тригонометрические приёмы для решения разных задач. В дальнейшем их усовершенствовали индийский математик Брамагупта (VI в.), узбекские математики аль-Каши и Улугбек (XII в.). В работах академика Леонарда Эйлера (XVIII в.) тригонометрия приобретает тот вид, который в основном имеет и в наше время.
Вычисление значений sin a, cos а и tg а
ЕЭ| Пусть в прямоугольном треугольнике ABC ZA = а, тогда ZB — 90° — а (рис. 467). Из определения синуса и косинуса следует:
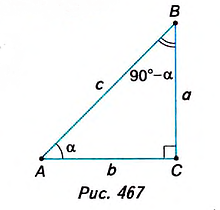
Как видим, между синусом и косинусом углов а и 90° — а, которые дополняют друг друга до 90°, существует зависимость: синус одного из этих углов равен косинусу другого.
Например:
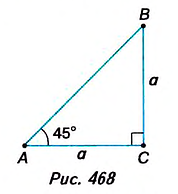
Найдём значения синуса, косинуса и тангенса для углов 45°, 30°, 60°. 1) Для угла 45°. Пусть ABC — прямоугольный треугольник с гипотенузой С и ے A = 45° (рис. 468). Тогда ے B = 45°. Следовательно, ∆ABC — равнобедренный. Пусть АС = ВС = а. Согласно теореме Пифагора,
2) Для углов 30° и 60°.
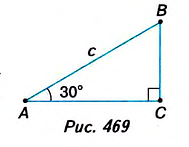
Пусть ABC — прямоугольный треугольник с гипотенузой с и ے A = 30″ (рис. 469). Найдём катеты АС и ВС.
ВС = 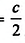
Согласно теореме Пифагора,
Тогда
Если в прямоугольном треугольнике ABC ے A = 30° (рис. 469),
Составим таблицу 35 значений синуса, косинуса и тангенса для углов 30°, 45°, 60°
Таблица 35
Из таблицы видно, что при увеличении угла синус и тангенс острого угла возрастают, а косинус — уменьшается. При уменьшении угла синус и тангенс острого угла уменьшаются, а косинус — увеличивается.
Пример №31
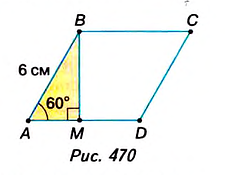
Сторона ромба равна 6 см, а один из его углов Найдите высоту ромба.
Решение:
Пусть ABCD — ромб (рис. 470), в котором АВ = 6 см, ے А = 60°. Проведём высоту ВМ. Из прямоугольного треугольника АВМ: 
При помощи инженерных калькуляторов (или программы «калькулятор» компьютера) либо специальных таблиц можно решить две задачи:
1) для заданного угла а найти sin a, cos а, tg а;
2) по заданному значению sin a, cos а, tg а найти угол а.
Если вы используете калькулятор, а угол указан в градусах и минутах, то минуты переведите в десятые доли градуса (разделите их на 60). Например, для угла 55°42° получите 55,7°. Если, например, для cos 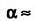
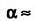
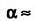
Значение sin a, cos а, tg а находим по таблицам.
Таблица синусов и косинусов (см. приложение 1) состоит из четырёх столбцов. В первом столбце слева указаны градусы от 0° до 45°, а в четвёртом — от 90° до 45°. Над вторым и третьим столбцами указаны названия «синусы» и «косинусы», а в нижней части этих столбцов — «косинусы» и «синусы».
Верхние названия «синусы» и «косинусы» отображают значения углов, которые меньше 45°, а нижние — больше 45°. Например, по таблице находим: sin34° 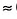
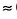
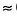
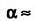
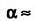
Таблица тангенсов (см. приложение 2) состоит из двух столбцов: в одном указаны углы от 0° до 89°, в другом — значения тангенсов этих углов.
Например, tg 19° 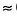
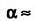
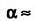
1. Вы уже знаете, что каждой градусной мере угла а прямоугольного треугольника соответствует единственное значение sin a, cos а, tg а. Поэтому синус, косинус и тангенс угла а являются функциями данного угла. Эти функции называются тригонометрическими функциями, аргумент которых изменяется от О° до 90°.
2. Уточним происхождение слова «косинус». Именно равенство cos а = sin (90° — а) явилось основой образования латинского слова cosinus — дополнительный синус, то есть синус угла, дополняющий заданный до 90°.
3. Первые таблицы синусов углов от 0° до 90° составил греческий математик Гиппарх (II в. до н. э.). Эти таблицы не сохранились. Нам известны только тригонометрические таблицы, помещённые в работе «Альмагест» александрийского учёного Клавдия Птолемея (II в.). Птолемей Также сохранились таблицы синусов и косинусов индийского учёного Ариаб-хаты (V в.), таблицы тангенсов арабских учёных аль-Баттани и Абу-ль-Вефа (X в.).
Как решать прямоугольные треугольники
Решить прямоугольный треугольник — это означает по заданным двум сторонам либо стороне и острому углу найти другие его стороны и острые углы.
Возможны следующие виды задач, в которых требуется решить прямоугольный треугольник по: 1) катетам; 2) гипотенузе и катету; 3) гипотенузе и острому углу; 4) катету и острому углу. Алгоритмы решения этих четырёх видов задач изложены в таблице 36.
Пример №32
Решите прямоугольный треугольник по гипотенузе с= 16 и углу а = 76°21′ (рис. 482).
Решение. Это задача третьего вида. Алгоритм её решения указан в таблице 38.
Решение многих прикладных задач основано на решении прямоугольных треугольников. Рассмотрим некоторые виды прикладных задач.
1. Задачи на нахождение высоты предмета, основание которого доступно.
Пример №33
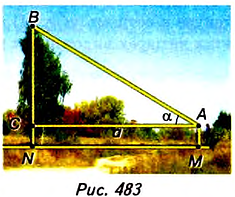
Найдите высоту дерева (рис. 483).
Решение:
На некотором расстоянии MN= а от дерева устанавливаем угломерный прибор AM (например, теодолит) и находим угол а между горизонтальным направлением АС и направлением на верхнюю точку В дерева. Из прямоугольного треугольника ABC получим: ВС= a • tg а. С учётом высоты угломерного прибора AM= h имеем формулу для вычисления высоты дерева: BN= о • tg а + h.
Пусть результаты измерения следующие: 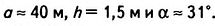
Тогда 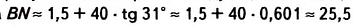
2. Задачи на нахождение высоты предмета, основание которого недоступно.
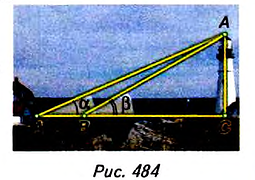
Пример №34
Найдите высоту башни, которая отделена от вас рекой (рис. 484).
Решение:
На горизонтальной прямой, проходящей через основание башни (рис. 484), обозначим две точки М и N, измерим отрезок MN= а и углы 
Почленно вычитаем полученные равенства:
Отсюда
Следовательно,
Прибавив к DC высоту прибора AM= Н, которым измеряли углы, получим
формулу для вычисления высоты башни:
Пусть результаты измерения следующие:
Тогда
3. Задачи на нахождение расстояния между двумя пунктами, которые разделяет препятствие.
Пример №35
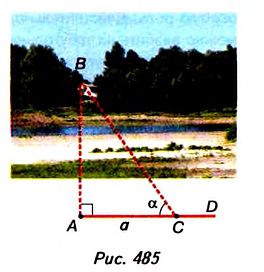
Найдите расстояние между пунктами А и В, разделёнными рекой (рис. 485).
Решение:
Провешиваем прямую 
Тогда АВ =
4. Задачи на нахождение углов (угла подъёма дороги; угла уклона; угла, под которым виден некоторый предмет, и т. д.).
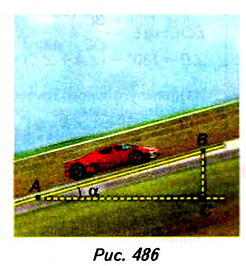
Пример №36
Найдите угол подъёма шоссе, если на расстоянии 200 м высота подъёма составляет 8 м.
Решение:
На рисунке 486 угол a — это угол подъёма дороги, АС— горизонтальная прямая. Проведём 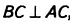
У вас может возникнуть вопрос: Почему в геометрии особое внимание уделяется прямоугольному треугольнику, хотя не часто встречаются предметы подобной формы?
Итак, поразмышляем. Как в химии изучают вначале элементы, а затем — их соединения, в биологии — одноклеточные, а потом — многоклеточные организмы, так и в геометрии изучают сначала простые геометрические фигуры — точки, отрезки и треугольники, из которых состоят другие геометрические фигуры. Среди этих фигур прямоугольный треугольник играет особую роль. Действительно, любой многоугольник можно разбить на треугольники (рис. 487).
Умея находить угловые и линейные элементы этих треугольников, можно найти все элементы многоугольника. В свою очередь, любой треугольник можно разбить одной из его высот на два прямоугольных треугольника, элементы которых связаны более простой зависимостью (рис. 488). Найти элементы треугольника можно, если свести задачу к решению этих двух прямоугольных треугольников. Проиллюстрируем это на примере.
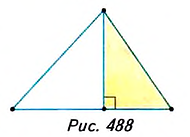
Пример №37
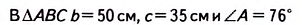
Решение:
Проведём высоту BD. Точка D будет лежать между точками А и С, поскольку ے A — острый и b> с.
Из прямоугольного треугольника ABD:
Из прямоугольного треугольника
Из прямоугольного треугольника BDC:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Параллелограмм
- Теорема синусов и теорема косинусов
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Площадь трапеции
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📸 Видео
Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Метрические соотношения в прямоугольном треугольнике - геометрия 8 классСкачать

МЕРЗЛЯК-8 ГЕОМЕТРИЯ. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ. ПАРАГРАФ-15 ТЕОРИЯСкачать

Прикладная задача по геометрии. Метрические соотношения в треугольнике.Скачать

Математика, 10-й класс, Метрические соотношения в треугольнике. Теорема синусовСкачать

2017-02-13 Геометрия 8 класс. Метрические соотношения в прямоугольном треугольникеСкачать

Прямоугольный треугольник. Метрические соотношения.Скачать

Метрические соотношения в треугольнике. Диафильм по математике для 8-го классаСкачать

Метрические соотношения в прямоугольном треугольнике. Соотношение 2.Скачать

Математика, 10-й класс, Метрические соотношения в треугольнике. Теорема косинусовСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

29. Метрические соотношения в прямоугольном треугольникеСкачать

Геометрия, 9 класс | Метрические соотношения в окружностиСкачать

Метрические соотношения в прямоугольном треугольникеСкачать
















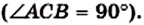
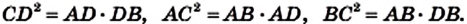
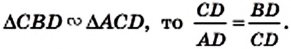 Отсюда
Отсюда 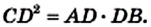
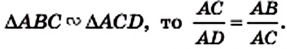 Отсюда
Отсюда 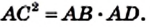
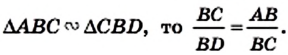 Отсюда
Отсюда 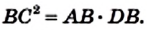
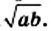
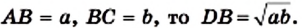
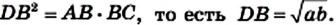
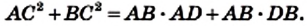
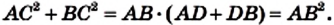
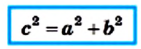
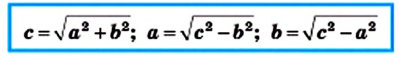

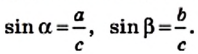
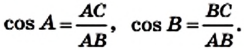
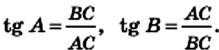
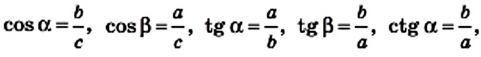
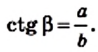
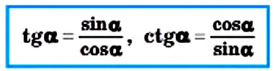

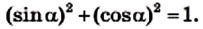
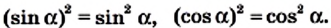
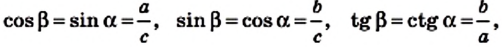

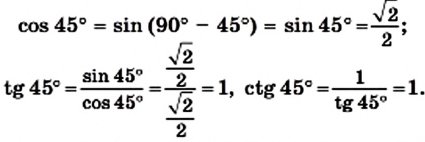
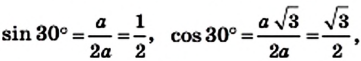
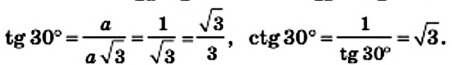
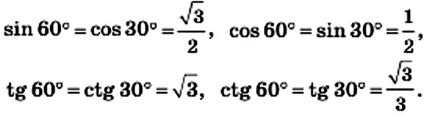
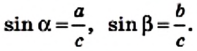
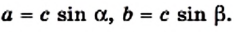
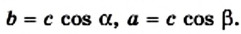
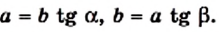
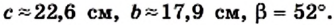
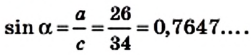
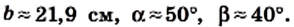
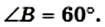
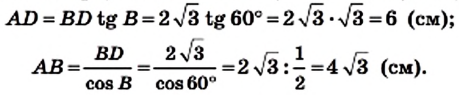
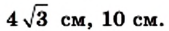
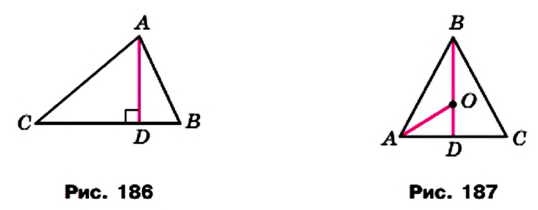
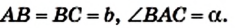
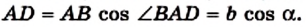
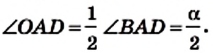
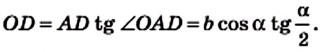
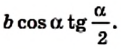


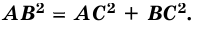
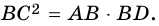
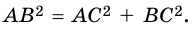
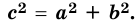
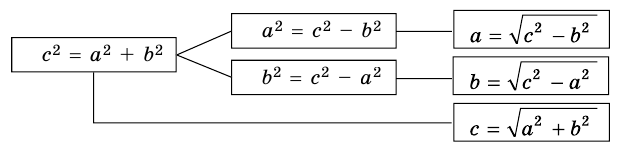
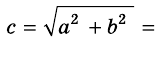
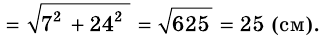
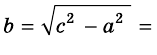
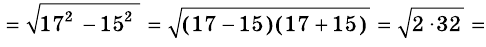
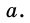
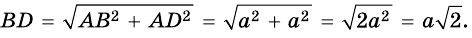
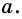
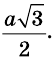
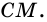
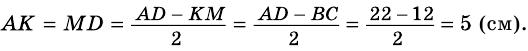
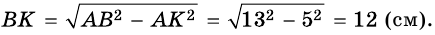
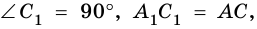
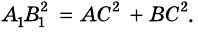
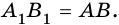

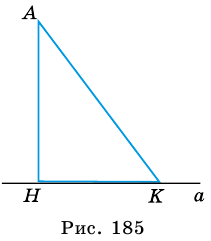
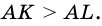
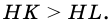
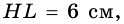
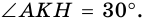
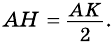
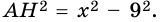
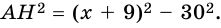
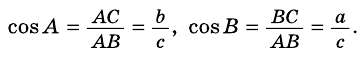
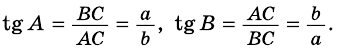
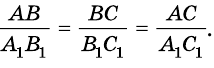

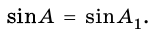
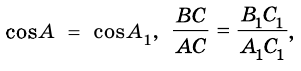
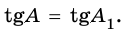
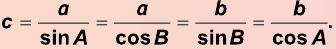
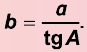
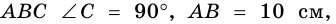
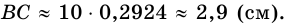
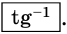
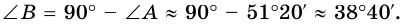
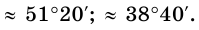
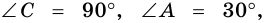
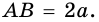
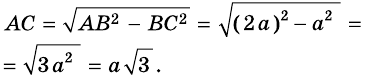
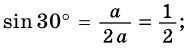
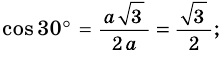
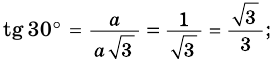
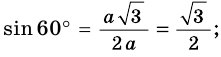
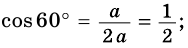
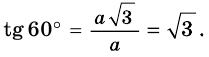
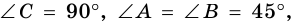

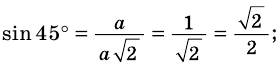
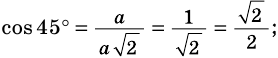
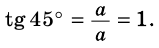
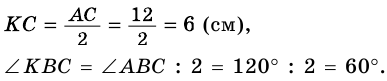
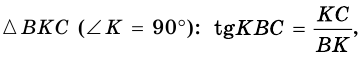
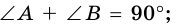
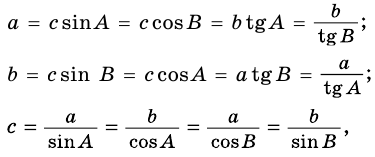



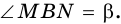
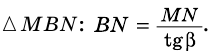
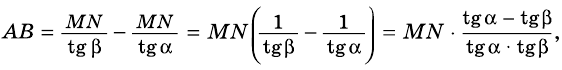
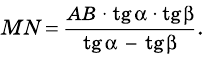
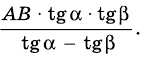
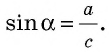
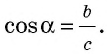
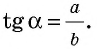
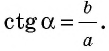
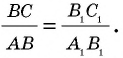
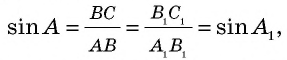
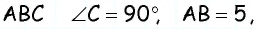
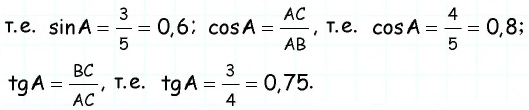
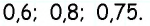
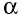
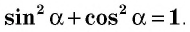
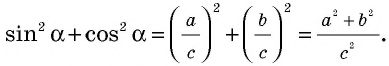
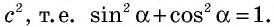
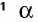
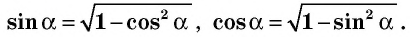
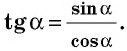
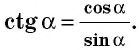
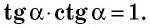
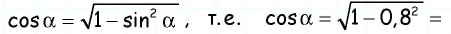
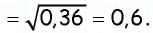
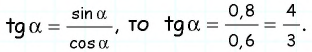
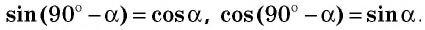
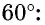
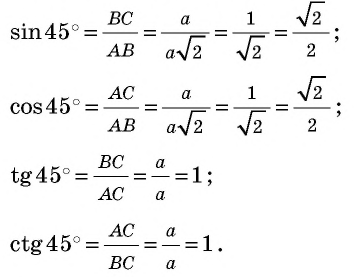
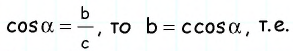
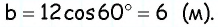


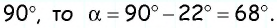
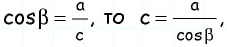
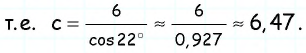

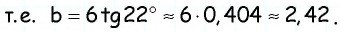
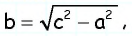
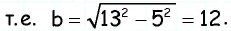
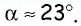

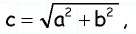
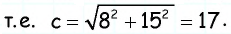

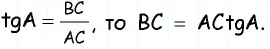
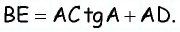
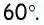
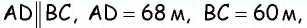
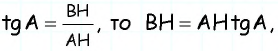
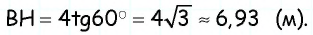
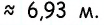
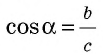
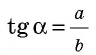
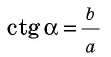
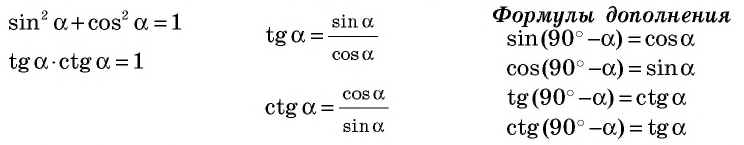

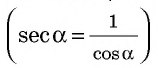
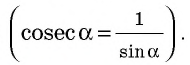
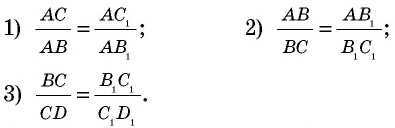
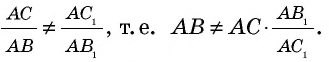
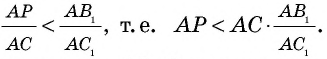
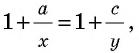
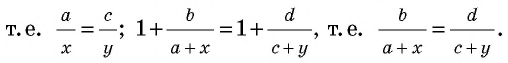
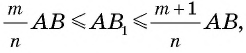
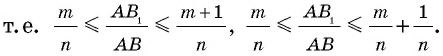
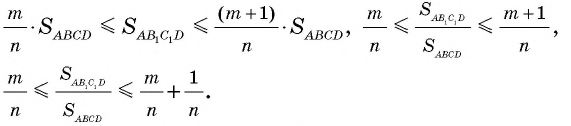
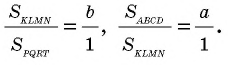
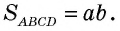
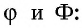
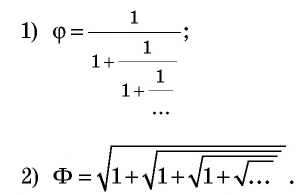
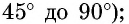
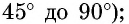
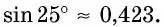
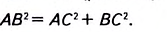
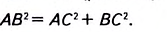
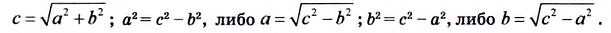
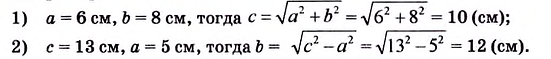
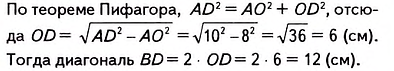
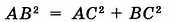 (рис. 415), тогда
(рис. 415), тогда 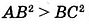 или АВ > ВС.
или АВ > ВС.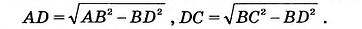 Поскольку в этих равенствах АВ = ВС (по условию), то AD = DC.
Поскольку в этих равенствах АВ = ВС (по условию), то AD = DC.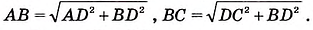 . В этих равенствах AD > DC. Тогда АВ > ВС.
. В этих равенствах AD > DC. Тогда АВ > ВС.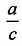 обозначают sin а и читают «синус альфа»;
обозначают sin а и читают «синус альфа»;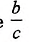 обозначают cos а и читают «косинус альфа»;
обозначают cos а и читают «косинус альфа»;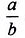 обозначают tg а и читают «тангенс альфа».
обозначают tg а и читают «тангенс альфа».