Медианы треугольника пересекаются в центре вписанной в него окружности

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Медианы треугольника пересекаются в центре вписанной окружности

Видео:Медианы треугольника пересекаются в точке М. Свойство пересекающихся хорд.Скачать

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Видео:22 Медианы треугольника пересекаются в одной точкеСкачать

Все, что нужно знать о треугольнике

При решении геометрических задач полезно следовать такому алгоритму. Во время чтения условия задачи необходимо

• Сделать чертеж. Чертеж должен максимально соответствовать условию задачи, так его основная задача помочь найти ход решения
• Нанести все данные из условия задачи на чертеж
• Выписать все геометрические понятия, которые встречаются в задаче
• Вспомнить все теоремы, которые относятся к этим понятию
• Нанести на чертеж все соотношения между элементами геометрической фигуры, которые следуют из этих теорем

Например, если в задаче встречается слова биссектриса угла треугольника, нужно вспомнить определение и свойства биссектрисы и обозначить на чертеже равные или пропорциональные отрезки и углы.

В этой статье вы найдете основные свойства треугольника, которые необходимо знать для успешного решения задач.

ТРЕУГОЛЬНИК.

Площадь треугольника.

1. ,

здесь — произвольная сторона треугольника, — высота, опущенная на эту сторону.

2. ,

здесь и — произвольные стороны треугольника, — угол между этими сторонами:

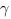
3. Формула Герона:

— здесь — длины сторон треугольника, — полупериметр треугольника,

4. ,

здесь — полупериметр треугольника, — радиус вписанной окружности.

Пусть — длины отрезков касательных.

Тогда формулу Герона можно записать в таком виде:

5.

6. ,

здесь — длины сторон треугольника, — радиус описанной окружности.

Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла делит треугольник на два треугольника, площади которых относятся как m:n:

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Медиана треугольника

— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.

Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший — радиусу описанной окружности.

Радиус описанной окружности в два раза больше радиуса вписанной окружности: R=2r

Длина медианы произвольного треугольника вычисляется по формуле:

,

здесь — медиана, проведенная к стороне , — длины сторон треугольника.

Биссектриса треугольника

— это отрезок биссектрисы любого угла треугольника, соединяющий вершину этого угла с противоположной стороной.

Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам:

Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.

Все точки биссектрисы угла равноудалены от сторон угла.

Высота треугольника

— это отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону, или ее продолжение. В тупоугольном треугольнике высота, проведенная из вершины острого угла лежит вне треугольника.

Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.

Чтобы найти высоту треугольника, проведенную к стороне , нужно любым доступным способом найти его площадь, а затем воспользоваться формулой:

Центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника.

Радиус описанной окружности треугольника можно найти по таким формулам:

— здесь — длины сторон треугольника, — площадь треугольника.

,

где — длина стороны треугольника, — противолежащий угол. (Эта формула вытекает из теоремы синусов).

Неравенство треугольника

Каждая сторона треугольника меньше суммы и больше разности двух других.

Сумма длин любых двух сторон всегда больше длины третьей стороны:

c» title=»a+b>c»/>

Напротив большей стороны лежит больший угол; напротив большего угла лежит большая сторона:

Если , то и наоборот.

Теорема синусов:

стороны треугольника пропорциональны синусам противолежащих углов:

Теорема косинусов:

квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:

Прямоугольный треугольник

— это треугольник, один из углов которого равен 90°.

Сумма острых углов прямоугольного треугольника равна 90°.

Гипотенуза — это сторона, которая лежит против угла 90°. Гипотенуза является наибольшей стороной.

Теорема Пифагора:

квадрат гипотенузы равен сумме квадратов катетов:

Радиус окружности, вписанной в прямоугольный треугольник, равен

,

здесь — радиус вписанной окружности, — катеты, — гипотенуза:

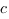
Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы:

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Определение синуса, косинуса , тангенса и котангенса прямоугольного треугольника смотрите здесь.

Соотношение элементов в прямоугольном треугольнике:

Квадрат высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу:

Квадрат катета равен произведению гипотенузы на проекцию катета на гипотенузу:

:

Катет, лежащий против угла равен половине гипотенузы:

Равнобедренный треугольник.

Биссектриса равнобедренного треугольника, проведенная к основанию является медианой и высотой.

В равнобедренном треугольнике углы при основании равны.

— угол при вершине.

и — боковые стороны,

и — углы при основании.

— высота, биссектриса и медиана.

Внимание! Высота, биссектриса и медиана, проведенные к боковой стороне не совпадают.

Правильный треугольник

(или равносторонний треугольник ) — это треугольник, все стороны и углы которого равны между собой.

Площадь правильного треугольника равна

,

где — длина стороны треугольника.

Центр окружности, вписанной в правильный треугольник, совпадает с центром окружности, описанной около правильного треугольника и лежит в точке пересечения медиан.

Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший — радиусу описанной окружности.

Если один из углов равнобедренного треугольника равен 60°, то этот треугольник правильный.

Средняя линия треугольника

— это отрезок, соединяющий середины двух сторон.

На рисунке DE — средняя линия треугольника ABC.

Средняя линия треугольника параллельна третьей стороне и равна ее половине: DE||AC, AC=2DE

Внешний угол треугольника

— это угол, смежный какому либо углу треугольника.

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

Тригонометрические функции внешнего угла:

Признаки равенства треугольников:

1 . Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2 . Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

3 Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Важно: поскольку в прямоугольном треугольнике два угла заведомо равны, то для равенства двух прямоугольных треугольников требуется равенство всего двух элементов: двух сторон, или стороны и острого угла.

Признаки подобия треугольников:

1 . Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами равны, то эти треугольники подобны.

2 . Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.

3 . Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.

Важно: в подобных треугольниках сходственные стороны лежат против равных углов.

Теорема Менелая

Пусть прямая пересекает треугольник , причем – точка ее пересечения со стороной , – точка ее пересечения со стороной , и – точка ее пересечения с продолжением стороны . Тогда

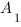
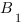
Видео:Точка пересечения медиан в треугольникеСкачать

Медианы треугольника пересекаются в центре вписанной окружности

Ключевые слова: основные линии треугольника, медиана, биссектриса, высота, средния линия, серединные перпендикуляры

Рассмотрим произвольный треугольник ABC:

a, b, c — стороны треугольника

$$m_a$$ — медиана к стороне a угла A

$$h_a$$ — высота к стороне a угла A

$$l_a$$ — биссектриса к стороне a угла A

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

• Медиана разбивает треугольник на два треугольника одинаковой площади.
• Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
• Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

• Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
• Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам.
• Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

• В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
• В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
• Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон
• Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.

Свойства серединных перпендикуляров треугольника

• Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
• Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

• Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Медианы треугольника пересекаются в центре вписанной в него окружности

Ключевые слова: основные линии треугольника, медиана, биссектриса, высота, средния линия, серединные перпендикуляры

Рассмотрим произвольный треугольник ABC:

a, b, c — стороны треугольника

$$m_a$$ — медиана к стороне a угла A

$$h_a$$ — высота к стороне a угла A

$$l_a$$ — биссектриса к стороне a угла A

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

• Медиана разбивает треугольник на два треугольника одинаковой площади.
• Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
• Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

• Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
• Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам.
• Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

• В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
• В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
• Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон
• Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.

Свойства серединных перпендикуляров треугольника

• Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
• Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

• Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

🎬 Видео

9 класс. Геометрия.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Две медианы треугольника пересекаются по прямым углом.Скачать

Теорема о трёх медианахСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

ЕГЭ-2020. №16. Вневписанная окружность🚀 Ортоцентр. Теорема Карно, Бланшета, Чевы, Менелая🔥Скачать

Медианы | Свойства медиан | Точка пересечения медиан на прямой ЭйлераСкачать

Медианы треугольника пересекаются в точке . Найдите длину медианыСкачать

егэ по математике c4, биссектрисы и медианыСкачать

№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

ОГЭ. Медианы треугольника и доп. построения! Где я оговорился?Скачать