Как найти ah в треугольнике

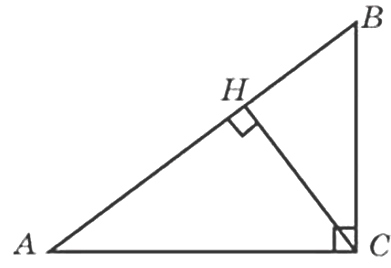
Решение прямоугольного треугольника. Продолжаем рассматривать задачи входящие в состав экзамена по математике. В этой статье разберём с вами несколько типов примеров. Они будут немного сложнее тех, которые мы с вами рассмотрели в статье « Прямоугольный треугольник. Часть 1 » . Но сложность эта относительна. Если вы эту статью не изучили, то сделайте это. На самом деле используются те же самые формулы. Вспомним их:

В треугольнике ABC угол C равен 90 градусов, AB = 20, sin A = 0,6.

Найдите высоту CH.

Сразу отметим, что все три треугольника ABC, ACH, CBH являются прямоугольными. Все элементы в данных треугольниках находятся так же с использованием основного тригонометрического тождества, формул из него следующих; определений синуса, косинуса, тангенса, котангенса. Кроме того могут использоваться признаки являются подобия.

Все прямоугольные треугольники, которые вы видите на рисунке подобны. Суть решения таких задач заключается в том, что один элемент можно рассматривать в разных треугольниках, на этом, и построено решение. Задачу можно решить в два-три действия, а можно в четыре-пять. Если вы сразу не увидели рациональный путь сразу – это не страшно.

Важно, чтобы вы понимали процесс решения и владели формулами.

Рассмотрим в данной задаче треугольник ACH:

Синус угла А нам известен, найдём АС. Сторону АС можем найти из треугольника АВС:

Найдём для начала cosA. Из основного тригонометрического тождества

sin 2 + cos 2 =1 получаем, что

Таким образом, AC=AB∙cosA=20∙0,8=16

Значит CH = AC∙sinA = 16∙0,6 = 9,6

В треугольнике ABC угол C равен 90 градусов, CH – высота, АВ = 123, tgA=1/9. Найдите АН.

Видно, что AH мы можем найти из треугольника AHC. То есть, процесс решения мы должны свести к тому, чтобы найти какие-либо элементы в этом треугольнике. Так как нам известен tgA=1/9, то мы можем найти cosA. Он нам пригодится для нахождения AC в треугольнике ABC и для нахождения AH в треугольнике AHC. Итак, найдём cosA.

Из основного тригонометрического тождества sin 2 +cos 2 =1 путём деления левой и правой частей на cos 2 A получим:

Теперь рассмотрим треугольник ABC:

Теперь рассмотрим треугольник AHC. П о определению косинуса в прямоугольном треугольнике: cosA = AH/AC,

Если вы сразу не видите, как решить подобную задачу, то поступайте следующим образом. Действуйте по принципу «ищу то, что могу». То есть исходя из условия смотрите – что вы можете найти, и вычисляйте элементы. Так шаг за шагом вы обязательно найдёте искомый элемент. И ещё обратите снимание на преобразования. Не обязательно вычислять промежуточные результаты (например cosA в данной задаче), можно оставлять полученное выражение. В дальнейшем будет удобно сокращать.

В треугольнике ABC AC=BC=25, sin A = 3/5 . Найдите AB .

Для начала найдём cosA. Из основного тригонометрического тождества sin 2 +cos 2 =1 получаем,

Теперь проведём высоту CH и рассмотрим прямоугольный треугольник ACH:

По определению косинуса:

cosA = AH/AC, откуда AH = AC∙cosA = 25∙0,8=20.

Рассмотрим равнобедренный треугольник ABC. Высота CH, проведённая к основанию, по свойству равнобедренного треугольника является медианой.

То есть AH = BH, и значит AB = 2 ∙ AH = 2∙20 = 40.

В треугольнике ABC AC = BC , AH — высота, tg ABC = 5/4. Найдите tg BAH.

Рассмотрим равнобедренный треугольник ABC. По свойству равнобедренного треугольника:

угол ABC равен углу BAC, значит tg ABC = tg BAC = 5/4.

Найдём ctg ABC. Известно, что tg ABC ∙ ctg ABC = 1, значит

Рассмотрим прямоугольный треугольник ABH. Из свойств прямоугольного треугольника:

tg BAH = ctg ABH = ctg ABC =0,8

В этой задаче не дан ни один линейный размер, поэтому пользуйтесь только тригонометрическими формулами (для нахождения углов).

Как видите, ничего особо сложного нет. Необходимо уметь оперировать формулами синуса, косинуса, тангенса и котангенса, знать основное тригонометрическое тождество, и всё! Задачу вы решите всегда.

Как уже говорил — если вы сразу не видите путь решения, то находите постепенно элемент за элементом исходя из того, что дано. Тогда искомый угол или сторону вы найдёте обязательно. Далее продолжим рассмотрение задач, не пропустите!

Сейчас предлагаю отдохнуть от математики, красивая музыка, красивая осень.

Видео:ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

Формулы для нахождения высоты треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Видео:В треугольнике ABC AC=BC=27, AH — высота, sin BAC= 2/3 . Найдите BH.Скачать

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты h_a, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Видео:В треугольнике ABC угол C равен 90°, CH – высота, AB = 13, тангенс A =1/5. Найдите AH.Скачать

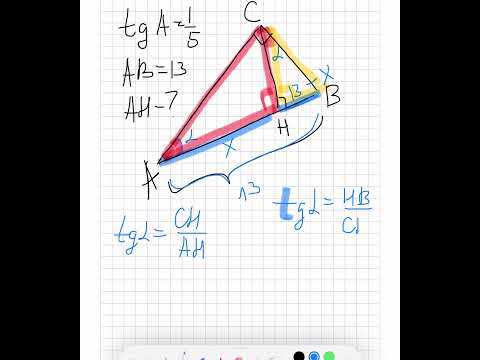
Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

Видео:В остроугольном треугольнике ABC высота AH равна 9√69 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Все формулы для треугольника

Видео:ОГЭ по математике. В треугольнике АБС известно три стороны. Найди косинус угла. (Вар.8) √ 16Скачать

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

Видео:В треугольнике ABC угол С=90, CH -- высота, AB=13, tgA=5. Найти BHСкачать

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

Видео:КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

Видео:Задача 6 №27357 ЕГЭ по математике. Урок 46Скачать

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

📸 Видео

Задание 6 ЕГЭ по математике. Урок 26Скачать

В треугольнике ABC проведены медиана BM и высота BH. Известно, что AC = 2 и BC = BM. Найдите AHСкачать

В треугольнике ABC AC = BC, AH – высота, AB = 5, sinBAC = 7/25 . Найдите BH.Скачать

Задача 6 №27350 ЕГЭ по математике. Урок 42Скачать

Уравнения стороны треугольника и медианыСкачать

Вычисляем высоту через координаты вершин 1Скачать

№762. Сторона равностороннего треугольника ABC равна а. Найдите: а) |AB+BC|Скачать

В треугольнике ABC угол C равен 90°, AB = 13, тангенс A = 1/5. Найдите высоту CH.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

В треугольнике АВС угол С равен 90°, CH — высота, BC = 3, синус A=1/6. Найдите АН.Скачать

Задание 6 ЕГЭ по математике. Урок 17Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать