Медиана треугольника является диаметром окружности

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Ваш ответ

Видео:Геометрия. Задача. Треугольник. Окружность.Скачать

решение вопроса

Видео:8. Медиана треугольника и её свойства.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,857
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

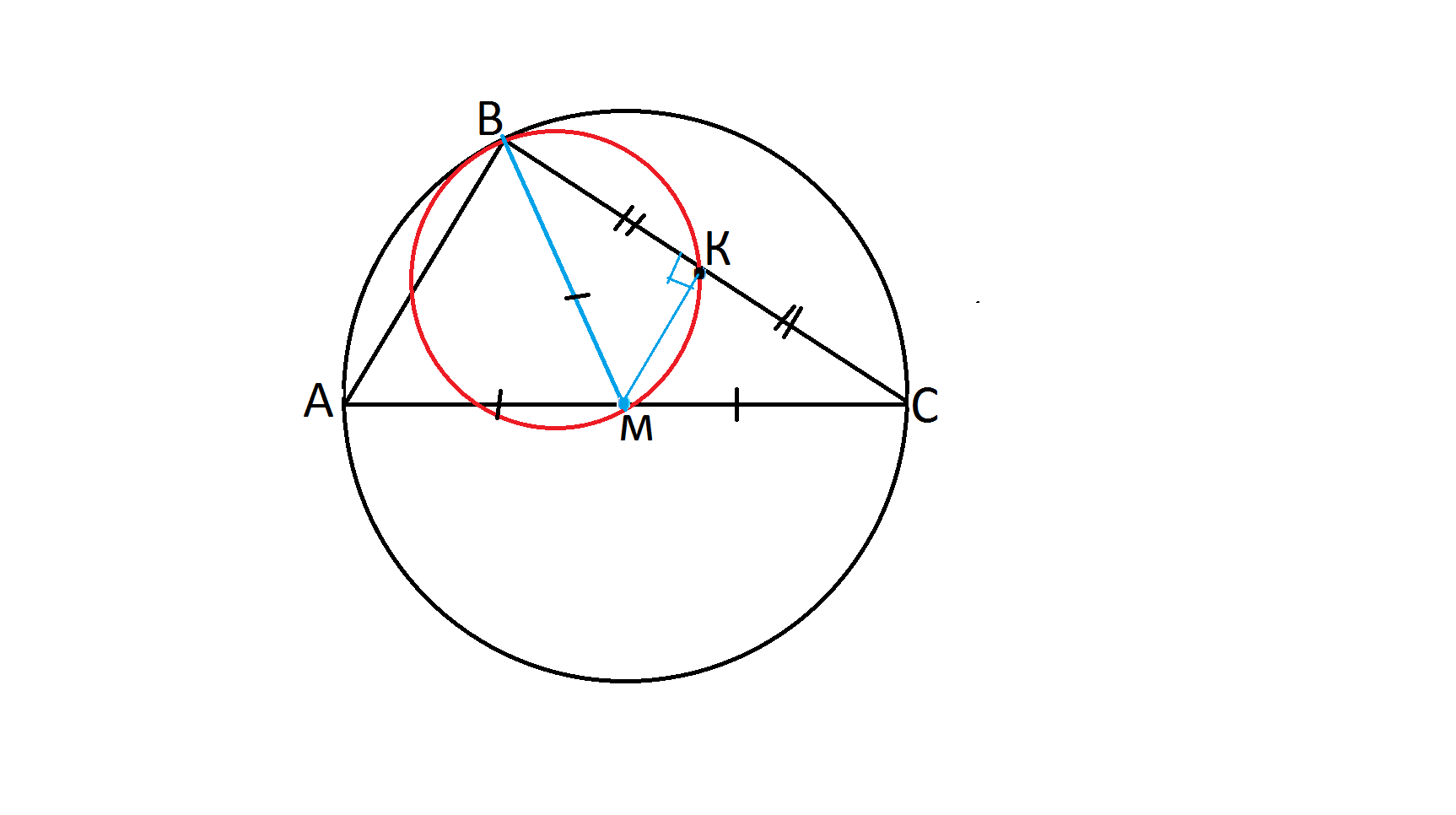
Медиана ВМ треугольника АВС является диаметром окружности, пересекающей сторону ВС в её середине?

Геометрия | 10 — 11 классы

Медиана ВМ треугольника АВС является диаметром окружности, пересекающей сторону ВС в её середине.

Найдите длину стороны АС, если радиус описанной около треугольника АВС окружности равен 7.

Сделаем рисунок и рассмотрим треугольник ВМС.

По условию ВК = КС,

МК — медиана треугольника ВМС.

Так как ВМ — диаметр описанной вокруг треугольника ВМК окружности, — треугольник ВКМ прямоугольный.

Тогда КМ — высота треугольника ВМС, но она же и медиана.

Треугольник, в котором высота является медианой — равнобедренный.

Треугольник ВМС — равнобедренный.

Так как АМ = МС, то ВМ = ВМ = МС.

Если медиана треугольника равна половине стороны, к которой она проведена, этот треугольник — прямоугольный.

Отсюда АС — диаметр описанной вокруг треугольника АВС окружности.

Видео:Построение медианы в треугольникеСкачать

В треугольнике АВС угол А равна альфа, угол В равно бета, ВС равна а?

В треугольнике АВС угол А равна альфа, угол В равно бета, ВС равна а.

Найдите длину стороны АС и радиус окружности, описанной около треугольника.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в ее середине?

Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в ее середине.

Найдите диаметр описанной окружности треугольника ABC.

Видео:🔥 Свойства МЕДИАНЫ #shortsСкачать

В треугольнике АВС сторона АВ является диаметром описанной около него окружности?

В треугольнике АВС сторона АВ является диаметром описанной около него окружности.

Найдите радиус этой окружности, если ВС = 15, АС = 8.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Сторона АС треугольника АВС равна 240?

Сторона АС треугольника АВС равна 240.

Противолежащий ей угол С равен 30 градусов.

Найти радиус окружности, описанной около этого треугольника.

Видео:Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать

Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BС в её середине?

Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BС в её середине.

Найдите этот диаметр, если диаметр описанной окружности треугольника ABC равен 8.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Длина медианы СМ треугольника АВС равнв 5см?

Длина медианы СМ треугольника АВС равнв 5см.

Окружность с диаметром СМ пересекает стороны АС и АВ в их серединах.

Найдите периметр треугольника АВС, если его площадь равнв 24 см ^ 2.

Видео:№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

В треугольнике АВС стороны равны 3, 5 и 6 ?

В треугольнике АВС стороны равны 3, 5 и 6 .

Найдите радиус окружности , описанной около треугольника.

Видео:Теорема о медианеСкачать

В треугольнике АВС угол В равен 60°, ВС = 3АВ?

В треугольнике АВС угол В равен 60°, ВС = 3АВ.

Около треугольника описана окружность радиуса 8√3 и в него же вписана окружность с центром в точке О.

Луч ВО пересекает сторону АС в точке М.

Видео:Медианы треугольника пересекаются в точке М. Свойство пересекающихся хорд.Скачать

Центр окружности описанной около треугольника АВС лежит на стороне АВ Радиус окружности равен 14, 5 Найдите АС, если ВС равен 21?

Центр окружности описанной около треугольника АВС лежит на стороне АВ Радиус окружности равен 14, 5 Найдите АС, если ВС равен 21.

Видео:ЗАДАЧА НА МЕДИАНУ ТРЕУГОЛЬНИКА. Примеры | ГЕОМЕТРИЯ 7 классСкачать

Около треугольника АВС описана окружность?

Около треугольника АВС описана окружность.

Продолжение биссектрисы СК треугольника АВС пересекает эту окружность в точке L, причем CL – диаметр данной окружности.

Найдите отношение отрезков ВL и АС, если синус угла ВАС равен ¼.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Медиана ВМ треугольника АВС является диаметром окружности, пересекающей сторону ВС в её середине?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

1) N лежит между М и К : MK = MN + NK = 7 + 5 = 12 (см) 2) К лежит между M и N : MK = MN — KN = 7 — 5 = 2 ( см) Ответ : 12см, 2см.

1)угол в = 60 а угол с = 90. Так как он является прямым следовательно вс = 60 + 90 = 150.

АL — биссиктриса , значит делит угол BAC по полам следовательно угол ВАС = ВАL + LAC = 26 + 26 = 52°. Сумма углов треугольника равна 180° следовательно угол ABC = 180 — BAC — CAL = 180 — 52 — 61 = 67° угол АВС = 67°.

Решение в приложении.

Сумму внутренних углов выпуклого многоугольника можно вычислить по формуле 180 * (n — 2). С другой стороны, если в многоугольнике n сторон, то сумма углов равна 135n. Приравняем эти два равенства, решим уравнение и найдём число сторон n. 180(n — 2..

Сумма противоположных углов четырех угольника равна 180° = > Угол С = 180° — 82° = 98°.

Сумма противоположных углов четырехугольника, вписанного в окружность равно 180 . Угол С = 180 — угол А = 180 — 82 = 98.

Ответ : 35°Объяснение : AA₁ ║ BB₁ ⇒ ∠(C₁B ; AA₁) = ∠B₁BC₁Рассмотрим ΔB₁BC₁ — прямоугольный∠B₁BC₁ = 90° — ∠B₁C₁B∠B₁BC₁ = 35°.

72 72 36 угол при вершине х, тогда угол при основанн будет 2х, но таких угла два, так как треугольник равнобедренный. Сумма углов в треуг. = 180, получаем уравнение 2х + 2x + x = 180 x = 36.

Заданную систему надо преобразовать : — первое уравнение умножить на 2 исвободный член перенести вправо, — во втором свободный член перенести вправо. Получаем : 1 вариант : складываем, 2х = 8, х = 8 / 2 = 4, у = 6 — х = 6 — 4 = 2. 2 вариант : выра..

💡 Видео

Медиана треугольника. Построение. Свойства.Скачать

Свойство окружности, описанной около равнобедренного треугольникаСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать