В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Определение медианы
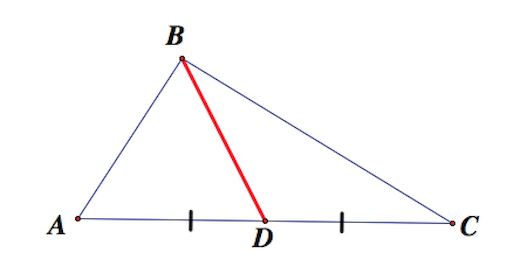
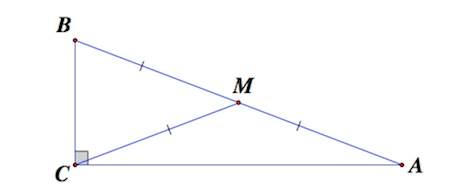
Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.
Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.
- AB = BC – боковые стороны;
- AC – основание.
Видео:Теорема о свойстве медианы равнобедренного треугольникаСкачать
Свойства медианы в равнобедренном треугольнике
Свойство 1
Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.
- BD – медиана и высота, опущенная на основание AC, а также биссектриса угла ABC.
- ∠ABD = ∠CBD
Свойство 2
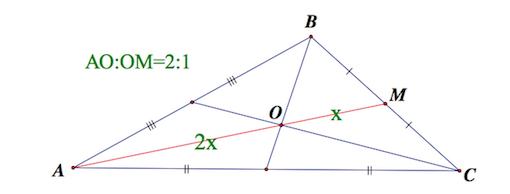
В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.
Свойство 3
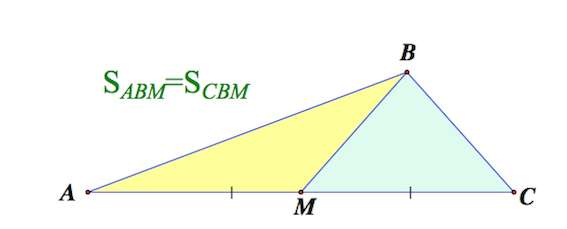
Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S1 = S2.
Свойство 4
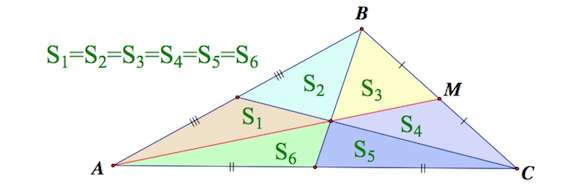
Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S1 = S2 = S3 = S4 = S5 = S6).
Свойство 5
Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:
Свойство 6
Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:
Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.
AF = CE, следовательно, AE = EB = BF = FC.
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Пример задачи
Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.
Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Медиана угла
Определение медианы
Медиана треугольника — это отрезок, который соединяет вершину треугольника с
серединой противоположной стороны. Медиана делит противолежащую сторону пополам.
Основание медианы — это точка пересечения медианы со стороной треугольника.
На рисунке 1 изображены три медианы, делящие каждая свою противолежащую
сторону пополам. Медианы BF, AH, CE соответственно делят пополам свои
противолежащие стороны AC, CB, AB.
Видео:8. Медиана треугольника и её свойства.Скачать

Элементы треугольника. Медиана
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Определение
Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны
Видео:№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Свойства
1. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины . Эта точка называется центром тяжести треугольника.
2. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника)
3. Медианы треугольника делят треугольник на 6 равновеликих треугольников
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы
5. Длина медианы треугольника вычисляется по формуле:
, где где
— медиана к стороне
;
— стороны треугольника
6. Длина стороны треугольника через медианы вычисляется по формуле:
, где
– медианы к соответствующим сторонам треугольника,
— стороны треугольника.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
🎬 Видео
Построение медианы в треугольникеСкачать

Равнобедренный треугольник. 7 класс.Скачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Внешний угол треугольникаСкачать

Уравнения стороны треугольника и медианыСкачать

№954. Медиана, проведенная к основанию равнобедренного треугольника, равна 160 см, а основаниеСкачать
Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Свойства равнобедренного треугольника. 7 класс.Скачать

№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

🔥 Свойства МЕДИАНЫ #shortsСкачать

№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать
Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать