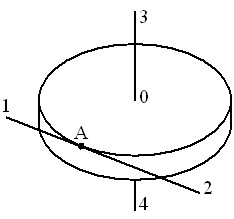
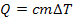Материальная точка движется по окружности с постоянной по модулю скоростью по часовой стрелке. В какой точке траектории ускорение тела направлено по стрелке?
Движение материальной точки по окружности с постоянной по модулю скоростью происходит благодаря наличию центростремительного ускорения, которое поворачивает вектор скорости. Это ускорение направлено вдоль радиуса окружности к ее центру. Направление стрелки соответствует направлению ускорения в точке 3.
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Равномерное движение материальной точки по окружности в физике с примерами
Содержание:
Равномерное движение материальной точки по окружности:
Более 5000 лет назад жрецы древнего Вавилона, наблюдая за Луной, определили такой хорошо известный нам интервал времени, как неделя. Как они это сделали? В чем особенность движения Луны? Встречается ли на Земле подобное движение?
Видео:Физика - движение по окружностиСкачать

Движение по окружности
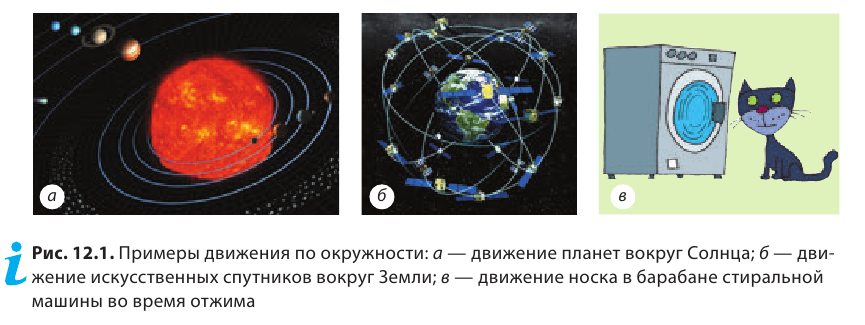
Попробуйте представить линию, вдоль которой движутся ребенок, кружащийся на карусели, носок в барабане стиральной машины во время отжима, кончик ножа блендера при изготовлении коктейля или смузи. Уверены, что вы легко определили: этой линией является окружность. Итак, в перечисленных случаях имеем дело с движением по окружности; простейшим является равномерное движение по окружности. Далее, говоря о равномерном движении по окружности любого физического тела, будем считать это тело материальной точкой. Равномерно по окружности движутся, например, кабинки колеса обозрения. Близким к равномерному движению по окружности является движение планет вокруг Солнца (рис. 12.1, а), естественного спутника (Луны) или искусственных спутников вокруг Земли* (рис. 12.1, б). Приведите примеры движения по окружности. В каких случаях это движение можно считать равномерным? Можно ли считать движение точек обода колеса велосипеда относительно его рамы равномерным движением по окружности? Обоснуйте свой ответ.
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь.
Определение периода вращения
Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные равные интервалы времени. Например, кончик секундной стрелки часов, двигаясь равномерно вдоль циферблата, повторяет свое движение через каждые 60 с (рис. 12.2).
Любое периодическое движение характеризуется такими физическими величинами, как период и частота. При равномерном движении по окружности говорят о периоде вращения и частоте вращения.
Период вращения — это физическая величина, равная времени, за которое материальная точка, равномерно движущаяся по окружности, совершает один оборот. Период вращения обозначают символом T. Единица периода вращения в СИ — секунда: [T]=c. Период вращения равен одной секунде, если за одну секунду совершается один оборот. Кончик секундной стрелки часов совершает один оборот за 60 с, поэтому период его вращения, как и каждой точки секундной стрелки, равен 60 с T =(60c .) Подумайте, каковы периоды вращения точек минутной и часовой стрелок часов. Когда взбивают молочный коктейль блендером, каждая точка его ножа за 30 с делает 6000 оборотов (рис. 12.3). Чтобы определить время одного оборота, нужно время вращения (t = 30 с) разделить на количество оборотов за это время (N = 6000): 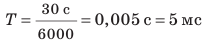
Определение частоты вращения
Указывая технические характеристики устройств, используют не период вращения, а частоту вращения (рис. 12.4). Частота вращения — это физическая величина, которая равна количеству оборотов за единицу времени. Частоту вращения обозначают символом n и определяют по формуле: 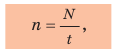
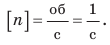
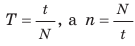
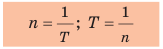
Как возникли единицы времени: сутки и неделя
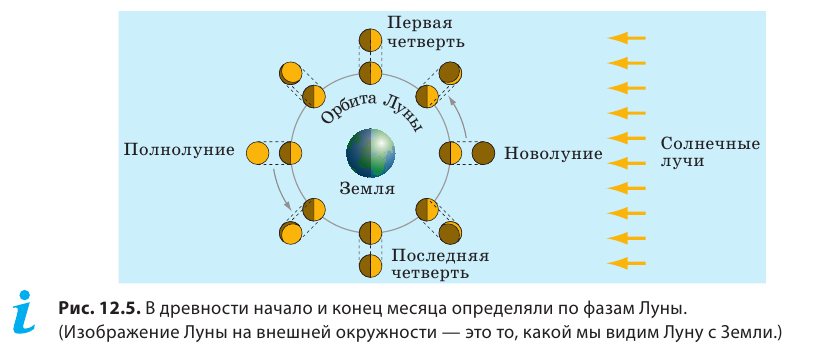
Как измерить время? Ответ на этот вопрос подсказала людям сама природа. Дело в том, что многие движения, происходящие в природе, являются периодическими, а период такого движения может служить единицей времени. Например, вращение Земли вокруг своей оси — периодическое движение. Ежедневный восход (закат) Солнца, обусловленный этим движением, подсказал нашим предкам единицу времени сутки, которые равны периоду вращения Земли вокруг своей оси. Несколько единиц времени были получены в древнем Вавилоне. Наблюдая за ночным небом, жрецы заметили, что «молодая» Луна появляется на небосклоне приблизительно каждые 28 суток. Периодическое рождение лунного диска служило своего рода вечными «часами». Так возникла единица времени месяц*. За это время Луна, вращаясь вокруг Земли, проходит полный цикл изменения фаз: новолуние, первая четверть, полнолуние, последняя четверть (рис. 12.5). Именно поэтому жрецы разделили лунный месяц на четыре части (поколичеству лунных фаз) и получили семь дней — единицу времени, которая называется неделя.
Определяем скорость равномерного движения по окружности
Кроме периода вращения и его частоты важной характеристикой движения по окружности является скорость движения. Если тело равномерно движется по окружности, то за время, равное периоду вращения t(=T, )тело совершает один оборот, то есть проходит путь, равный длине окружности. Длину окружности l можно вычислить по известной вам из математики формуле: 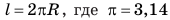
Сейчас, как правило, используют понятие календарного месяца, который не зависит от фаз Луны и длится от 28 до 31 суток.
Именно об этой скорости идет речь, когда, например, определяют скорость движения человека, кружащегося на карусели, говорят о скорости полета искусственных спутников Земли и т. д.
Итоги:
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь. Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные одинаковые интервалы времени. Период вращения T — физическая величина, равная времени, в течение которого материальная точка, равномерно движущаяся по окружности, совершает один оборот. Единица периода вращения в СИ — секунда (с). Частота вращения n — это физическая величина, которая равна количеству оборотов за единицу времени. Единица частоты вращения в СИ — оборот в секунду (об/с, или 1/с). Период вращения T и частоту вращения n определяют по формулам: 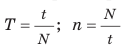
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Равномерное и неравномерное движение
- Равномерное движение
- Неравномерное движение
- Вращательное движение тела
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Тестовые задания по физике 1 семестр
Читайте также:
|
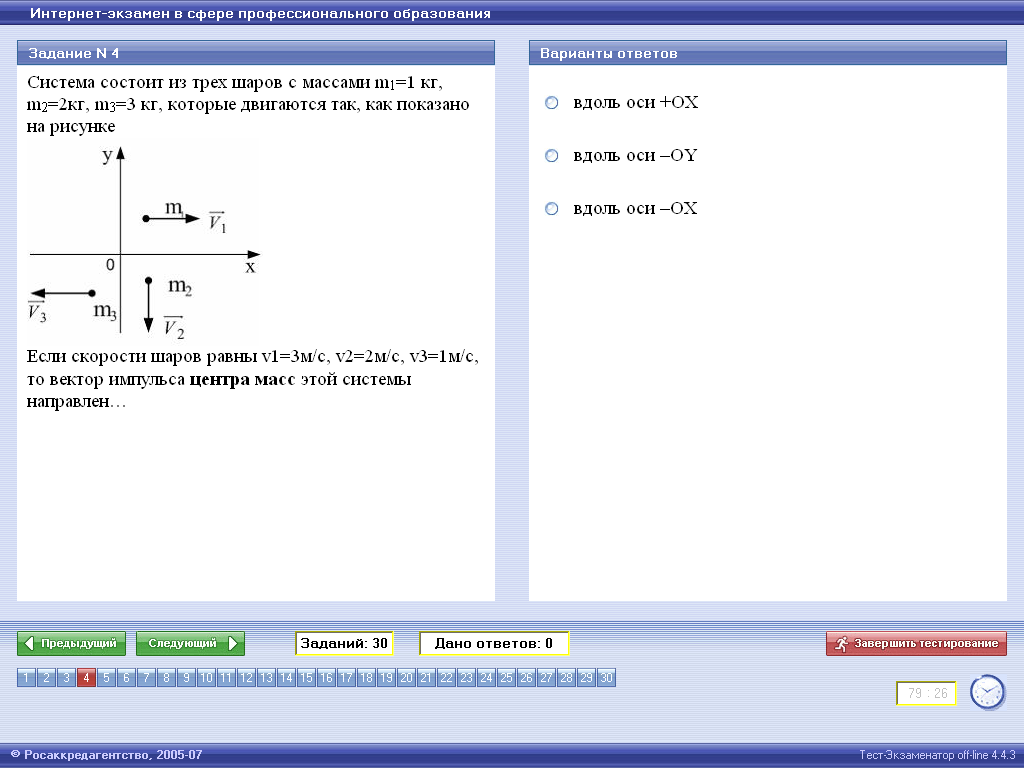
| 7. Система состоит из трех шаров с массами m 1=1 кг, m2=2кг и m3=3кг, которые движутся так, как показано на рисунке. Если скорости шаров равны v1=3м/с, v2=2м/с v3 =1м/с, то вектор импульса центра масс этой системы направлен: 1)вдоль оси + ОY 2)вдоль оси +ОХ 3)вдоль оси –ОY |
8. 
9. 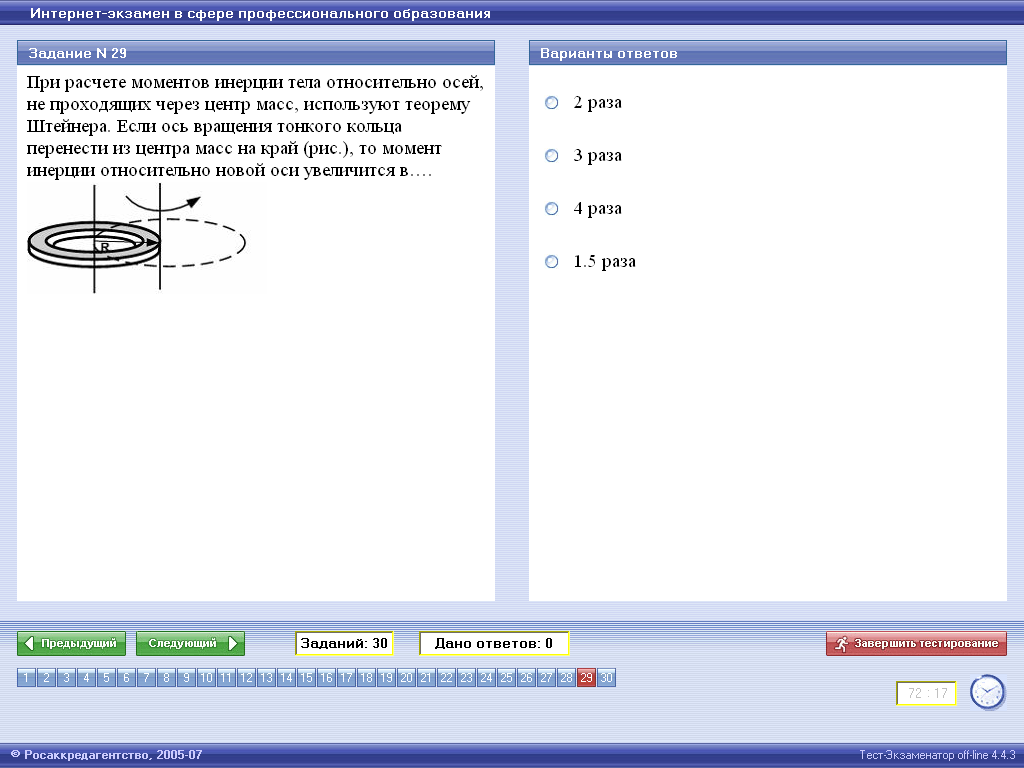
1) в 2 раза 2) в 3 раза 3) в 4 раза 4) в 5 раз
10. Hа частицу, находящуюся в начале координат, действует сила, вектор которой определяется выражением F= 2i + 3j , где i и j единичные вектор декартовой системы координат. Работа, совершенная этой силой при перемещении частицы в точку с координатами (5;0) равна…
1) 15 Дж 2) 5 Дж 3) 10 Дж 4) 4 Дж
11. 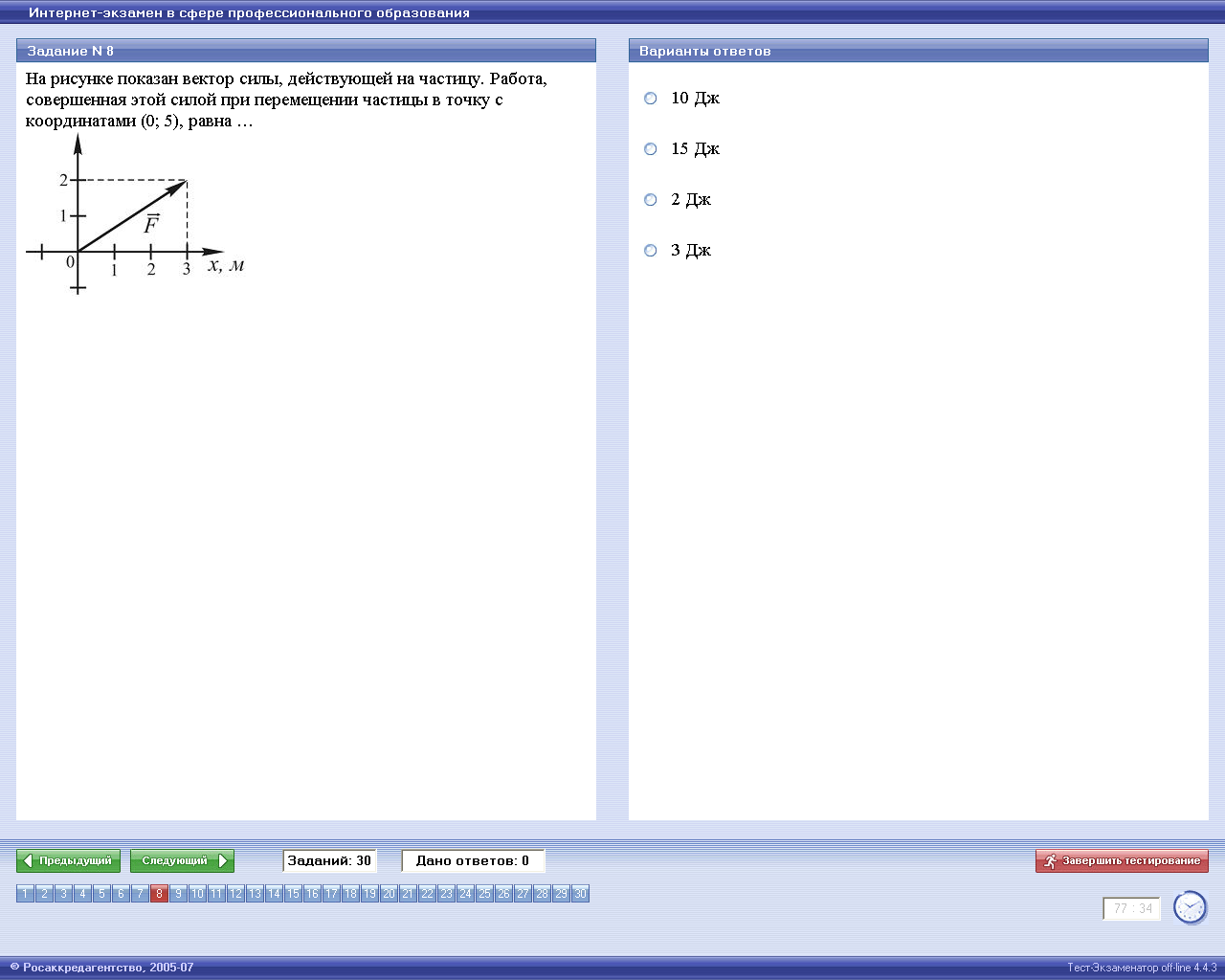
1) 5 Дж 2)15 Дж 3) 10 Дж 4) 25 Дж
12. Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину. Если он повернет шест из горизонтального положения в вертикальное, то частота вращения в конечном состоянии
1) увеличится 2) уменьшится 3) не изменится
13. График зависимости величины тангенциального ускорения от времени для равномерного движения тела по окружности изображен на рисунке:
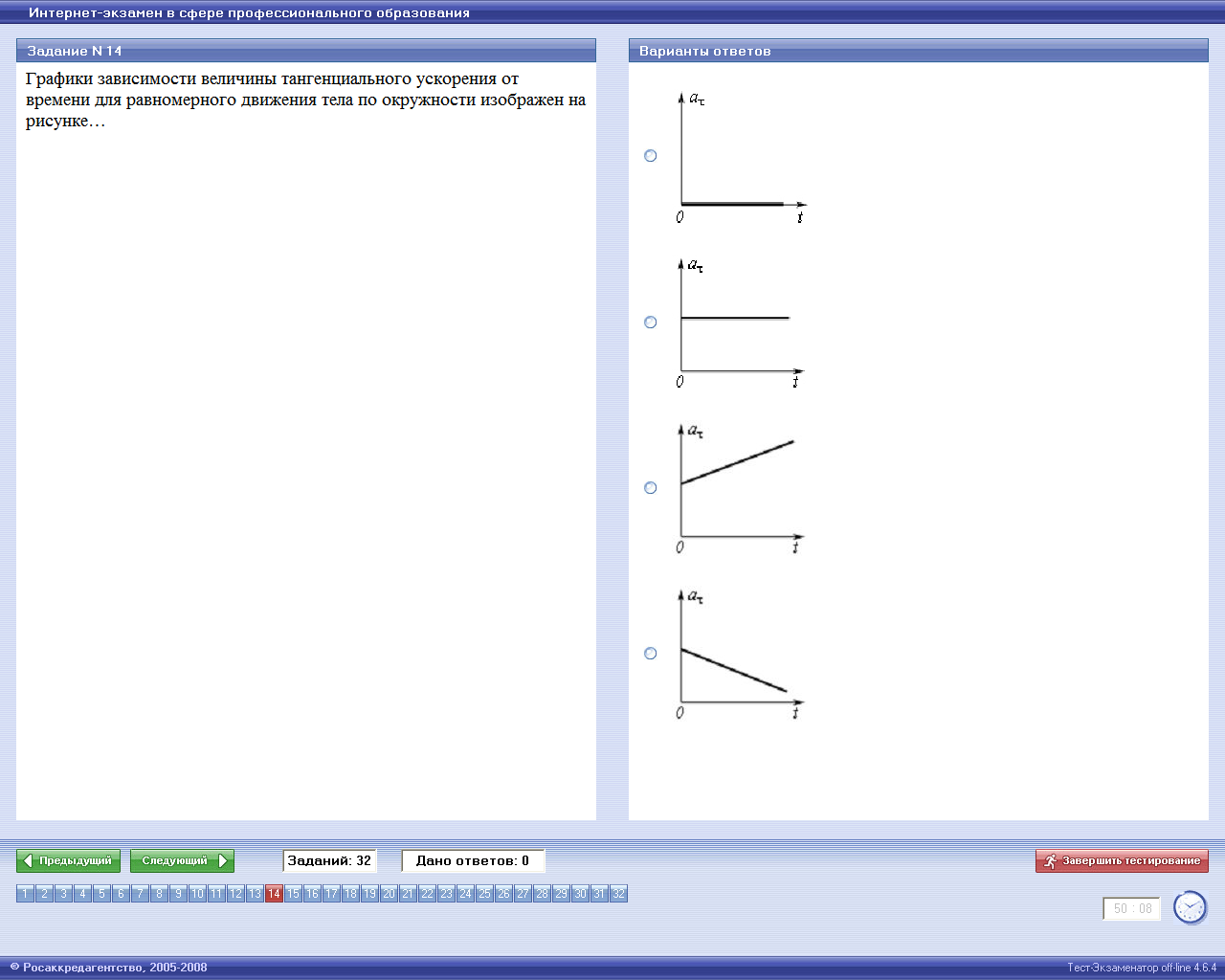


14. Закон изменения угла поворота со временем имеет вид φ = 3t 3 + 5t 2 +7. Угловая скорость изменяется по закону:
1) ω = 3t 3 + 10t +7 2) ω = 9t 3 + 10t +7
3) ω = 9t 2 + 10t 4) ω = 3t 2 + 5t +1
15. Средняя скорость движущегося тела направлена:
1) вдоль радиус-вектора 2) вдоль пути
3) вдоль вектора перемещения 4) вдоль касательной к траектории
16. Касательное ускорение точки, движущейся по кривой, ответственно за:
1) изменение вектора скорости по направлению
2) изменение вектора скорости по величине
3) изменение радиус-вектора
4) изменение радиуса кривизны траектории
17. Закон изменения угловой скорости материальной точки имеет вид ω = 9t 2 . Угловое ускорение точки определяется выражением:
1) ε = 18t 2) ε = 9t 3) ε = 9 4) ε = 18 5) ε = 9t 2
18. Механически изолированной системой тел называется:
1) система, в которой тела взаимодействуют друг с другом только по законам механики
2) система, в которой тела не взаимодействуют друг с другом
3) система, у которой отсутствует механическое взаимодействие с окружающими телами
4) система, в которой тела могут перемещаться без трения
5) система, находящаяся в состоянии невесомости
19. Автомобиль движется равномерно и прямолинейно со скоростью υ. Равнодействующая всех сил, приложенных к автомобилю:
1) не меняется со временем и направлена по направлению движения
2) не меняется со временем и направлена против направления движения
3) не меняется со временем и равна 0
4) меняется со временем и направлена по направлению движения
5) меняется со временем и направлена против направления движения
20. Кинетическая энергия тела массой 5 кг, движущегося вдоль оси Х по закону X = 8 + 6t + 6t 2 в момент времени 2с равна:
1) 1300 2) 1450 3) 2250 4) 2200 5) 1000
21. Моментом силы называют величину, численно равную:
1) произведению силы на квадрат расстояния до оси вращения
2) произведение силы на длину перпендикуляра, опущенного из центра вращения на направление силы
3) произведение силы на расстояние до оси вращения
4) произведение силы на угловую скорость
22. На неподвижный бильярдный шар налетел другой такой же с импульсом P = 0,5 кг·м/с. После удара шары разлетелись под углом 90° так, что импульс первого шара стал P1 = 0,3 кг·м/с. Импульс второго шара после удара…
1) 0,4 кг·м/с 3) 0,5 кг·м/с 2) 0,3 кг·м/с 4) 0,2 кг·м/с
23. Материальная точка вращается в горизонтальной плоскости относительно неподвижной оси с угловым ускорением ε = 2t 2 , при t= 0 ω0 = 0. Закон изменения угловой скорости имеет вид:
1) ω = 3/2 t 3 2) ω = 2/3 t 3 3) ω = 4 t 4) ω = 4 t 3
24. При движении материальной точки вектор скорости все время перпендикулярен вектору ускорения. Точка движется:
2) по криволинейной траектории равномерно
3) по криволинейной траектории равноускоренно
4) по окружности равномерно
5) по окружности равноускоренно
25. Материальная точка движется равноускоренно по окружности, лежащей в горизонтальной плоскости, против часовой стрелки. Вектор угловой скорости направлен:
1) по касательной к траектории против направления движения
2) по касательной к траектории по направлению движения
3) вниз по оси вращения
4) вверх по оси вращения
26. Точка движется согласно уравнению r= 4t 2 ix +3t iy + 1 iz. Ускорение точки в момент времени 2с равно:
1) 8 2) 11 3) 12 4) 7 5) 6
27. Тело вращается по закону φ = 6t 2 + 8t +7. Угловое ускорение в момент времени t= 5с равно:
1) 197 2) 68 3) 12 4) 60 5) 6
28. Момент инерции тела зависит от:
1) массы тела и его размеров
2) момента сил, действующих на тело
3) углового ускорения и массы тела
4) суммы сил, действующих на тело
5) массы тела и распределения массы относительно оси вращения
29. Материальная точка движется так, что радиус-вектор меняется со временем по закону 
30. Материальная точка движется равноускоренно по криволинейной траектории. Вектор мгновенной скорости направлен:
1) по касательной к траектории
2) к центру кривизны траектории
3) по направлению вектора перемещения
4) вдоль радиуса кривизны от центра
31. Тело движется согласно уравнению x= A + Bt + Ct 2 . Сила, действующая на него с течением времени:
1) возрастает 2) убывает
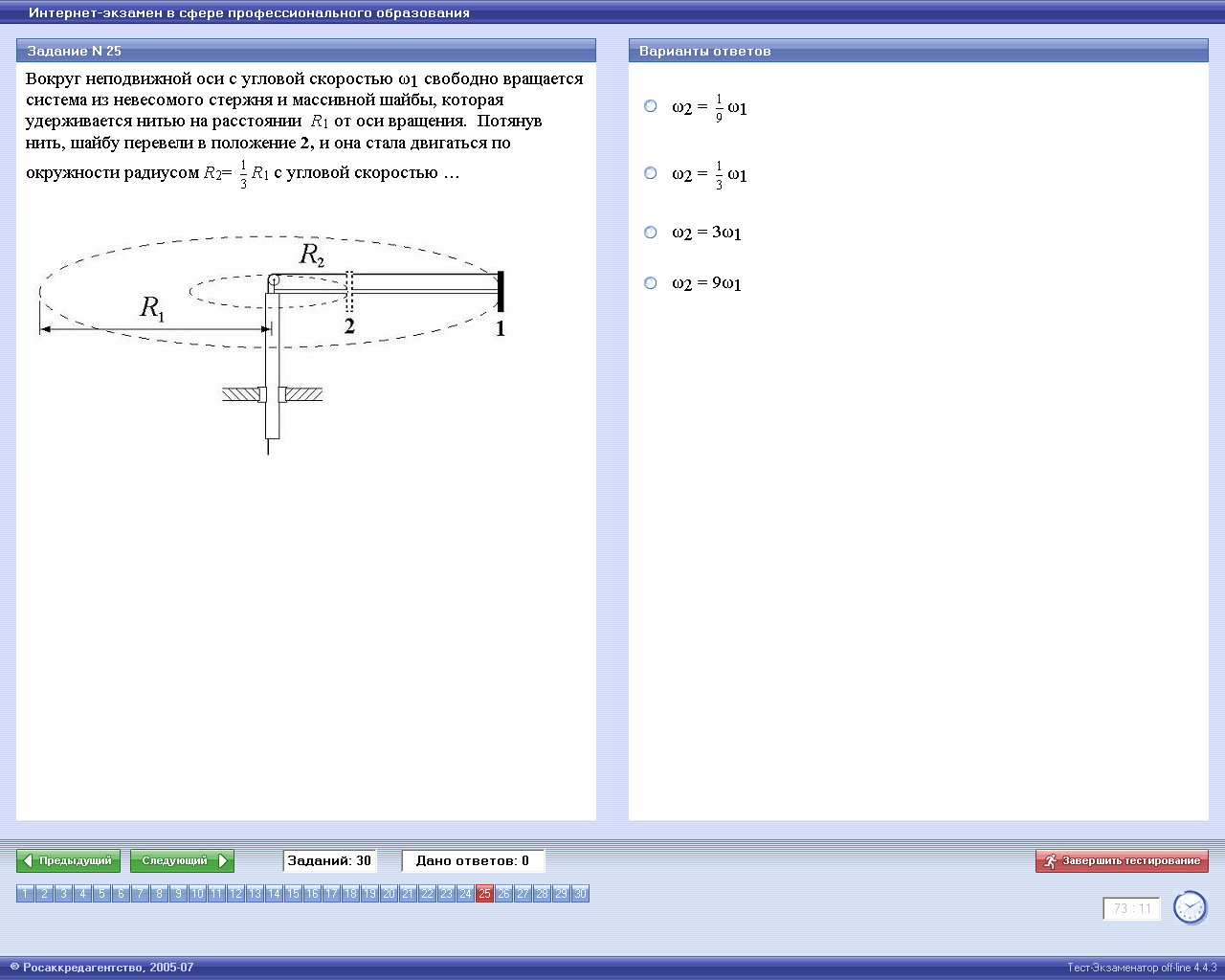
32. Вокруг неподвижной оси с угловой скоростью ω1 свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии R1 от оси вращения. Потянув нить, шайбу перевели в положение 2, и она стала двигаться по окружности радиусом R2=1/3R1 с угловой скоростью…
33. 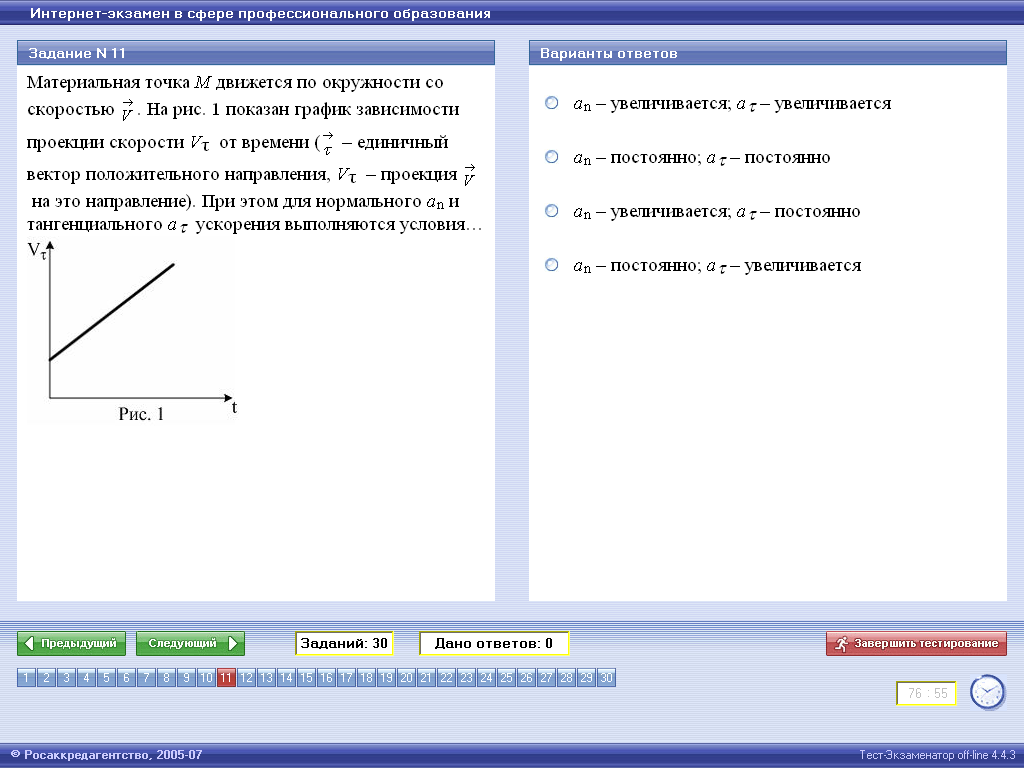
1) aτ — уменьшается ; an — постоянно
2) aτ — постоянно; an— постоянно
3) aτ — увеличивается; an — увеличивается
4) aτ — постоянно; an — уменьшается
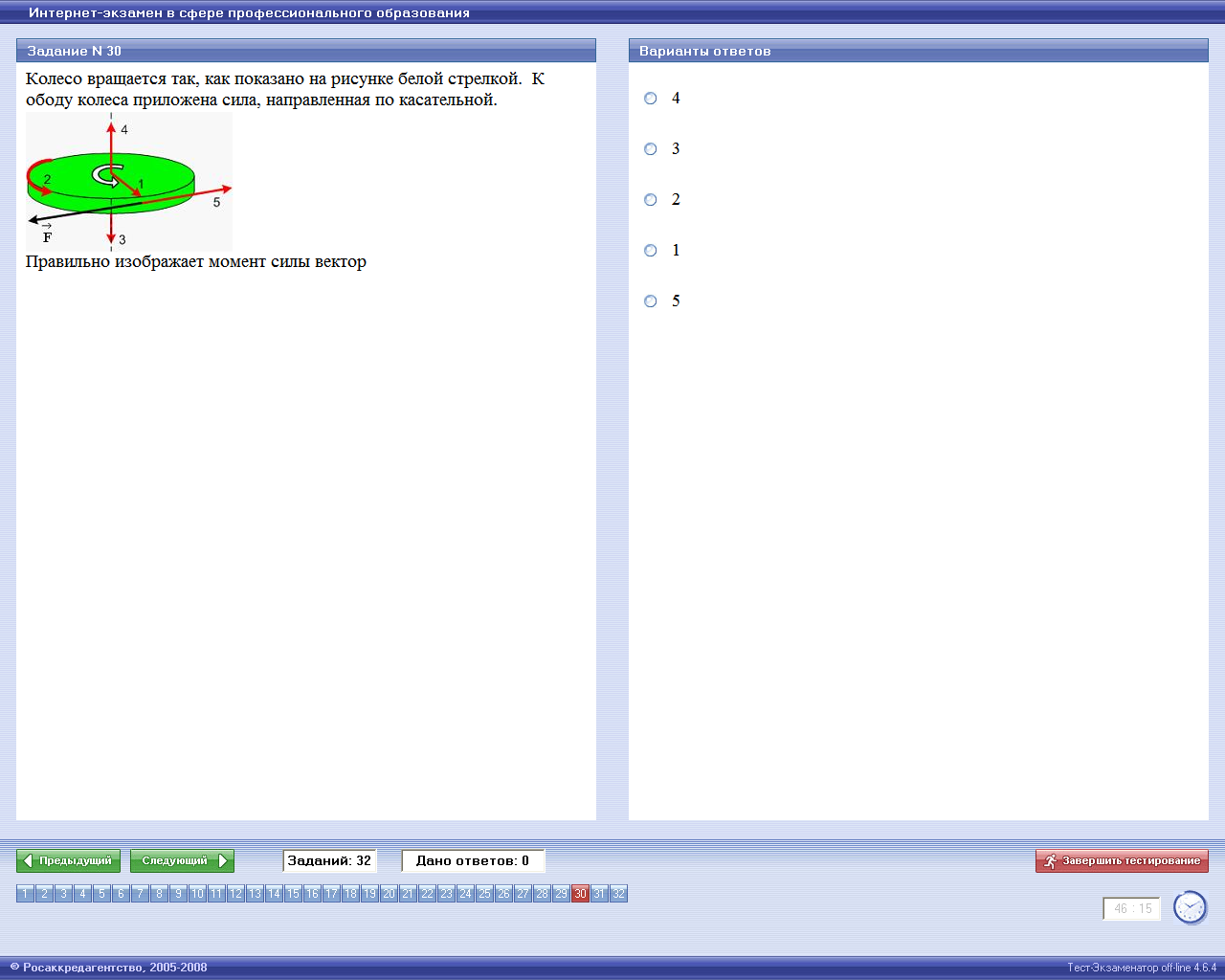
34. 
35. 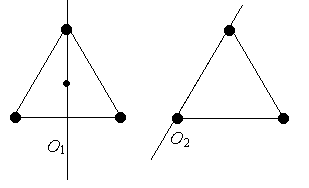
1) I1>I2 2) I1 Т2 > Т3. Распределение скоростей молекул в сосуде с температурой Т1, будет описывать кривая…
52. 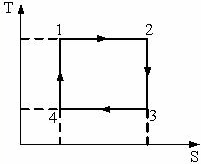
1) 1- 2 2) 2- 3 3) 3- 4 4) 4- 1
53. 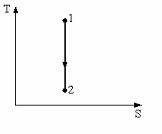
1) изобарным расширением
2) изотермическим расширением
3) адиабатным сжатием
4) адиабатическим расширением
54. 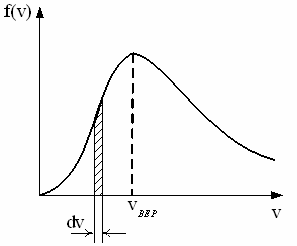
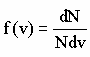
молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала. Если, не меняя температуры взять другой газ с большей молярной массой и таким же числом молекул, то …
1) максимум кривой сместится влево в сторону меньших скоростей
2) величина максимума увеличится
3) площадь под кривой уменьшится
4) площадь под кривой не изменится
5) максимум кривой сместится вправо в сторону больших скоростей
6) величина максимума уменьшится
55. 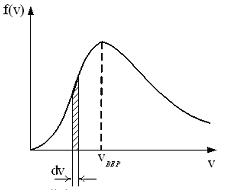
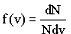
1) при понижении температуры величина максимума уменьшается
2) при понижении температуры площадь под кривой уменьшается
3) положение максимума кривой зависит как от температуры, так и от природы газа.
56. При какой температуре плотность идеального газа будет в 1,5 раз больше его плотности при температуре 402 К, если давление газа постоянно. Ответ выразите в кельвинах, округлив до целых чисел.
1) 268 К 2) 603 К 3) 201 К 4) 628 К
57. Газ аргон, количество вещества которого равно10 моль, при неизменном объеме нагрели от температуры 100 0 С до 400 0 С. Внутренняя энергия газа увеличилась в
1) в 1,8 раз 2) в 2 раза 3) в 4 раза 4) в 4,6 раз
58. Удельная теплоемкость вещества — это:
1) количество теплоты, необходимое для нагревания единицы массы вещества на 1 К;
2) количество теплоты, которое сообщается одному молю вещества для его нагревания на 1К;
3) отношение количества теплоты, переданного телу, к изменению температуры тела;
4) его теплоемкость при постоянном объеме.
59. Минимальное расстояние, на которое сближаются центры двух молекул при столкновении – это
1) средняя длина свободного пробега молекулы
2) эффективное сечение молекулы
3) средний диаметр молекулы
4) эффективный диаметр молекулы
60. Барометрическая формула устанавливает
1) зависимость давления газа от высоты при постоянной температуре
2) зависимость давления газа от его концентрации при постоянной температуре
3) зависимость давления газа от температуры
4) зависимость, при которой происходит выравнивание концентрации газа по всему объему
61. Каков физический смысл универсальной газовой постоянной
1) она численно равна работе, которую необходимо совершить над одним килограммом газа, чтобы изменить его температуру на один градус;
2) она равна произведению постоянной Больцмана на число Авогадро, то есть R = kNA
3) физического смысла нет
4) она численно равна работе, которую необходимо совершить над одним молем газа при постоянном давлении, чтобы изменить его температуру на один градус
62. Появление сил трения между слоями жидкости, движущимися параллельно друг другу с различными скоростями, называется .
1) внутренним трением 3) жидкостным трением
2) скоростным трением 4) влажным трением
63. В процессе обратимого адиабатического нагревания постоянной массы идеального газа его энтропия …
1) не меняется 2) увеличивается 3) уменьшается
64. Политропическим называется процесс, происходящий при постоянной(ом)
1) температуре 2)давлении 3) объеме 4) теплоемкости
65. Указать формулировку третьего начала термодинамики (теорема Нернста)
1) тепло, полученное системой, идёт на приращение её внутренней энергии и на производство внешней работы.
2) вне зависимости от начального состояния изолированной системы в конце концов в ней установится термодинамическое равновесие, при котором все части системы будут иметь одинаковую температуру.
3) Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система
4) Невозможен круговой процесс, единственным результатом которого было бы производство работы за счёт охлаждения теплового резервуара.
66. 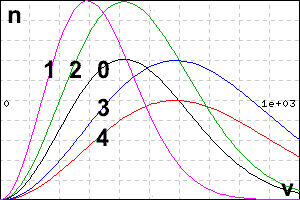
1) Кривая 1 (фиолетовая)
2) Кривая 2 (зелёная)
3) Кривая 3 (синяя)
4) Кривая 4 (красная)
67. Один моль вещества равен.
1) количеству вещества массой 12 граммов;
2) количеству вещества системы, которая содержит столько же структурных элементов, сколько содержится в изотопе углерода С12 массой 12 граммов;
3) количеству атомов и молекул, которое содержится в любом веществе массой 12 граммов;
4) количеству структурных элементов в изотопе углерода С]2 массой 12 граммов.
68. Распределение Максвелла по скоростям определяет:
1) количество молекул dN, обладающих скоростями, лежащими в определенном диапазоне скоростей dυ;
2) долю молекул dN/N, обладающих скоростями, лежащими в интервале dυ около значения скорости υ;
3) долю молекул из общего их числа, имеющих кинетические энергии, заключенные в интервале от Е до E+dE;
4) количество молекул dN, обладающих энергиями, лежащими в определенном диапазоне энергий dE;
69. Закон равномерного распределения энергии по степеням свободы говорит о том, что на каждую степень свободы частиц, находящихся в тепловом равновесии при температуре Т, приходится энергия:
70. Единицей какой физической величины является моль
1) единицей массы
2) единицей количества молекул
3) единицей количества любых частиц в веществе
4) единицей количества вещества
71. Каков физический смысл коэффициента вязкости?
1) он численно равен импульсу, передаваемому между слоями в единицу времен через единичную площадку, расположенную параллельно слоям при градиенте скорости упорядоченного движения, равном единице
2) он численно равен силе трения, возникающей между слоями в единицу времен через единичную площадку, расположенную параллельно слоям при градиенте скорости упорядоченного движения, равном единице;
3) он численно равен количеству теплоты, переносимому в единицу времен через единичную площадку, расположенную параллельно слоям при единичном градиенте температуры;
4) он численно равен массе, переносимой в единицу времен через единичную площадку, расположенную перпендикулярно направлениям переноса, при единичном градиенте температуры.
72. Как зависит длина свободного пробега от давления?
1) с ростом давления она увеличивается;
2) с ростом давления при постоянной температуре она уменьшается;
3) не зависит от давления;
4) зависит от давления при высоких температурах.
73. Цикл Карно — это:
1) цикл, совершаемый любой тепловой машиной;
2) такой круговой процесс, при котором тепловая машина все получаемое тепло от нагревателя превращает в работу;
3) круговой процесс, при котором система совершает работу только за счет изменения своей внутренней энергии;
4) прямой круговой процесс, при котором выполненная системой работа максимальна.
74. В ходе какого процесса передача количества теплоты идеальному газу равна работе газа над внешними телами:
1) адиабатического 3) изобарического
2) изотермического 4) изохорического
75. Почему, если газ нагревается в ходе изохорического процесса, изменение внутренней энергии равно сообщенному количеству теплоты
1) первый закон термодинамики не выполняется
2) нет теплообмена с окружающей средой
3) газ не совершает работу
4) количество теплоты нельзя рассчитать по формуле
76. Физический смысл энтропии:
1) энтропия — это мера беспорядка;
2) энтропия — это функция состояния;
3) изменение энтропии не зависит от протекания процесса;
4) энтропия изолированной системы, совершающей обратимый цикл, не изменяется.
77. Как связано изменение внутренней энергии dU тела с работой А, совершенной телом над внешними телами и количеством теплоты, переданным телу?
1)dU = dA + dQ; 3) dU = dQ — dА;
2) dU=dA — dQ; 4) dU = dQ.
78. Переход тепла от тела, имеющего меньшую температуру, к телу, имеющему большую температуру,
1) может происходить, если другие тела совершают работу;
2) никогда не может происходить в силу первого закона термодинамики;
3) не может происходить в силу законов теплопередачи;
4) никогда не может происходить в силу закона сохранения энергии.
79. Что называется фазой?
1) часть системы, которая является однородной по своим химическим и физическим свойствам;
2) величина, характеризующая состояние термодинамической системы в любой момент времени и в любой точке пространства;
3) часть системы, ограниченную поверхностью раздела, с одинаковыми физическими свойствами во всех своих точках;
4) совокупность систем, которые можно охарактеризовать одними и теми же термодинамическими параметрами.
80. Чем с молекулярно-кинетической точки зрения жидкости отличаются от газов?
1) скоростью движения молекул;
2) размерами молекул;
3) молекулы жидкости находятся почти вплотную друг к другу;
4) молекулы жидкости движутся более упорядоченно.
81. За 4 с маятник совершает 8 колебаний. Частота колебаний равна:
1) 0,5 2) 2 3) 4 4) 8 5) 32
82. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OX со скоростью 500м/с, имеет вид ξ =0,01sin(10 3 t- κx). Волновое число κ равно…
1)2м -1 2)5м -1 3)0,5м -1
83. Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами А0. При разности фаз ∆ φ=π амплитуда результирующего колебания равна…
84. Амплитуда гармонических колебаний, совершаемых материальной точкой вдоль прямой, равна 0,5 м. Путь, пройденный точкой за период колебаний, равен:
1) 2м 2) 1,5м 3) 1м 4) 0,5м 5) 0м
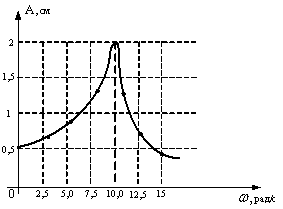
85. На рисунке представлена зависимость амплитуды вынужденных колебаний груза на пружине с жёсткостью k = 10 Н/м от частоты внешней силы. При малом затухании в системе масса колеблющегося груза равна…
1) 1 т 2) 0,01 кг 3) 0,1 кг 4) 10 кг
86. При свободных колебаниях маятника максимальное значение потенциальной энергии равно 10 Дж, максимальное значение кинетической энергии равно 10 Дж. Полная механическая энергия изменяется в пределах:
1) от 0 до 10 2) от 0 до 20 3) 0т 10 до 20
4) не изменяется и равна 10 5) не изменяется и равна 20
87. Складываются 2 гармонического колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной…
1) p/2 2) p/4 3) 0 4) p
88. Если длину математического маятника увеличить в 2 раза, а массу уменьшить в 2 раза, то частота колебаний:
1) уменьшится в 4 раза 2) увеличится в 2 раза
3) увеличится в 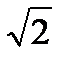
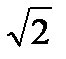
89. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид ζ =0,01sin (10 3 t -2х). Период равен.
1) 1 мс 2) 2 мс 3) 6,28 мс
90. Грузик массы m колеблется на пружине с амплитудой A и угловой частотой ω. Какова максимальная скорость грузика?
1) Aω 2 2) ω 2 A/2 3) Aω 4) Aω 2 m
91. Космический корабль летит со скоростью V=0,8 с (с – скорость света в вакууме). Один из космонавтов медленно поворачивает метровый стержень из положения 1, перпендикулярного направлению движения корабля, в положение 2, параллельное этому направлению. Тогда длина этого стержня с точки зрения наблюдателя, находящегося на Земле…
1) уменьшается от 1 метра до 0,6 3) не изменяется
2) увеличивается от 1 метра до 1,6 4) уменьшается от 1 метра до 0
92. Космический корабль пролетает мимо вас со скоростью 0,8 с. По вашим измерениям его длина равна 90 м. В состоянии покоя его длина наиболее близка к…
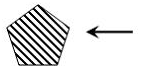
93. На борту космического корабля нанесена эмблема виде геометрической фигуры. Из-за релятивистского сокращения длины эта фигура изменяет свою форму. Если корабль движется в направлении, указанном на рисунке стрелкой, со скоростью, сравнимой со скоростью света, то в неподвижной системе отсчета эмблема примет форму, указанную на рисунке…
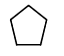
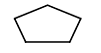
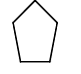
94. Космический корабль с двумя космонавтами на борту, один из которых находится в носовой части ракеты, другой — в хвостовой, летит со скоростью V=0,8c. Космонавт, находящийся в хвостовой части ракеты, производит вспышку света и измеряет промежуток времени t1 за который свет проходит расстояние до зеркала, укрепленного у него над головой, и обратно к излучателю. Этот промежуток времени с точки зрения другого космонавта.
1) меньше, чем t1 в 1,67 раз
3) больше, чем t1 в 1,25 раз
4) меньше, чем t1 в 1,25 раз
95. Космический корабль движется относительно Земли со скоростью υ, соизмеримой со скоростью света с. Длительность некоторого процесса в космическом корабле, измеренная по часам этого корабля, составляет Δt0. Длительность этого процесса Δt измеренная по часам, находящимся на Земле, определяется соотношением.
1) Δt=Δt0 2) Δt=Δt0 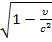
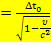
96. Некоторое событие длилось на Земле 2 мкс. Сколько времени оно длилось для наблюдателя, пролетающего мимо Земли в ракете со скоростью с/2 (где с –скорость света в вакууме) относительно Земли?
1) 2,3 мкс 2) 1,73 мкс 3) 1,4 мкс 4) 2,8 мкс
97. Некоторое событие длилось на Земле 2 мкс. На сколько процентов изменилась длительность этого события с точки зрения наблюдателя, находящегося в ракете, пролетающей относительно Земли со скоростью с/2 (где с – скорость света в вакууме) ?
1) Увеличилась на 15% 3) уменьшилась на 15%
2) Увеличилась на 40% 4) уменьшилась на 40%
98. На Земле период колебаний пружинного маятника равен Т. Чему он будет равен в ракете, движущейся относительно Земли со скоростью с/2 (где с – скорость света в вакууме) ?
1) 0,5 Т 2) 2Т 3) 1,15 Т 4) Т
99. Скорость света в инерциальных системах отсчета
1) зависит только от скорости движения источника света
2) не зависит ни от скорости приемника света, ни от скорости источника света
3) зависит только от скорости приемника света
4) зависит и от скорости приемника света, и от скорости источника света
100. Формулы специальной теории относительности необходимо использовать при описании движения
1) Только микроскопических тел, скорости которых близки к скорости света
2) Только макроскопических тел, скорости которых близки к скорости света
3) Любых тел, скорости которых близки к скорости света
4) Любых тел, скорости которых малы по сравнению со скоростью света
Дата добавления: 2014-10-31 ; просмотров: 144 ; Нарушение авторских прав
📹 Видео
Центростремительное ускорение. 9 класс.Скачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Равноускоренное движение по окружности. Видеоурок 51. Физика 10 классСкачать

Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Физика | Равномерное движение по окружностиСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

9 класс | Кинематика | Движение по окружности. Постоянная по модулю скоростьСкачать
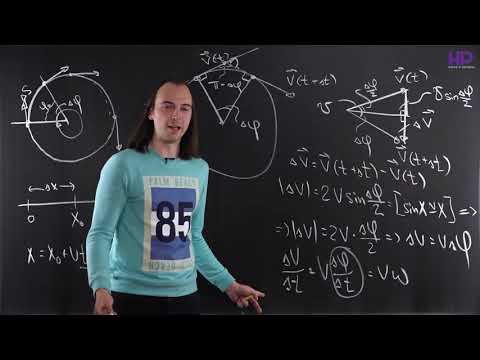
Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Твердое тело vs Материальная точка | Физика ЕГЭСкачать

Урок 89. Движение по окружности (ч.1)Скачать

Кинематика за 8 минСкачать


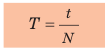

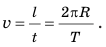
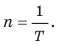

 равномерного криволинейного движения
равномерного криволинейного движения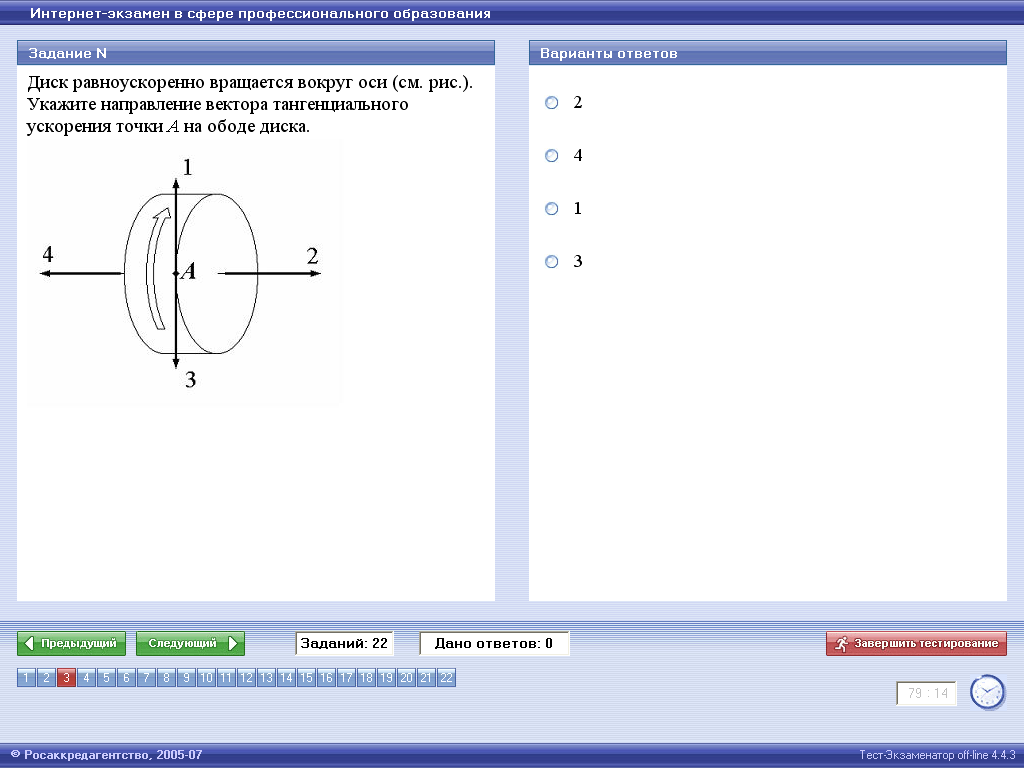
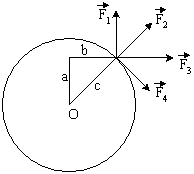 К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечо силы F1 равно…
К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечо силы F1 равно…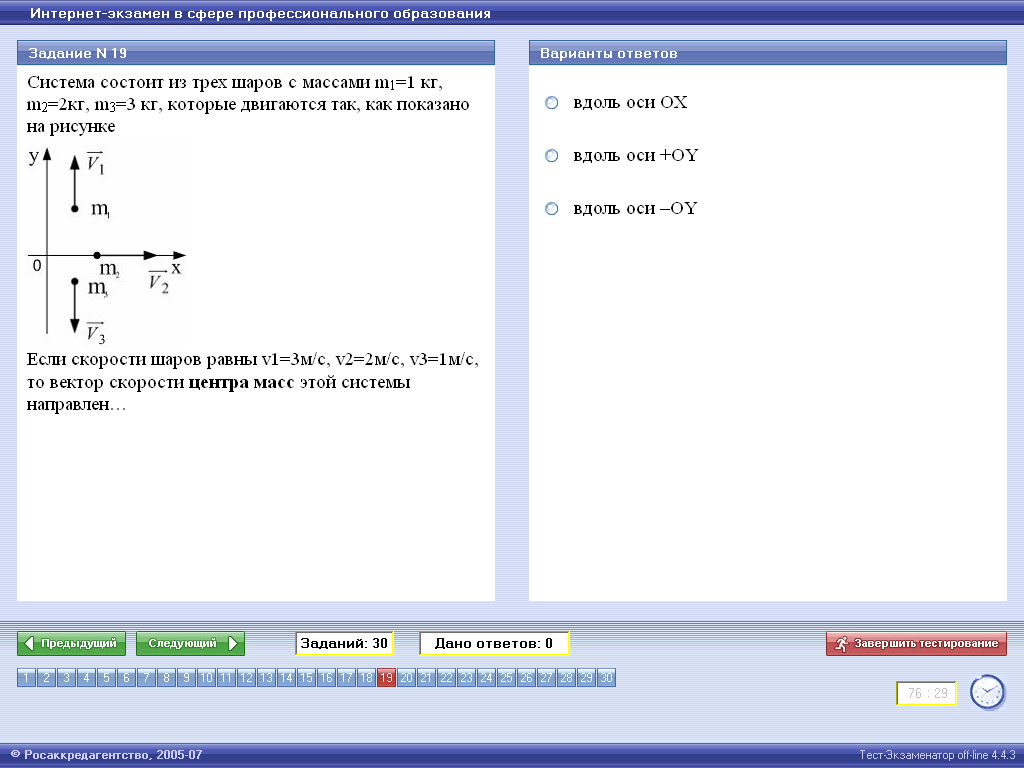 20 м/с 2) 10 м/с 3) 14 м/с 4) 40 м/с
20 м/с 2) 10 м/с 3) 14 м/с 4) 40 м/с