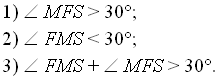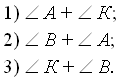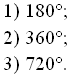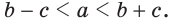Проверка знаний по геометриии в 7 классе по теме «Углы треугольника»
Просмотр содержимого документа
«Тест по теме «Углы треугольника»»
Тест по теме «Углы треугольника»
Для данного треугольника МFS верно…
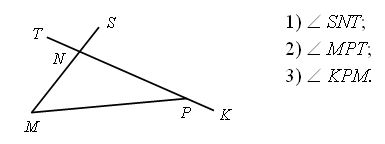
Для данного треугольника MNP внешним является угол…
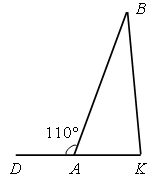
Для данного треугольника ABK сумма каких углов равна 110°?
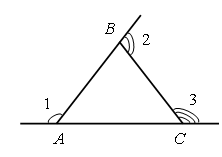
В треугольнике сумма внешних углов, взятых по одному при вершине, равна…
В прямоугольном треугольнике АСВ СН – высота, а CD – биссектриса. Тогда угол DCH равен…
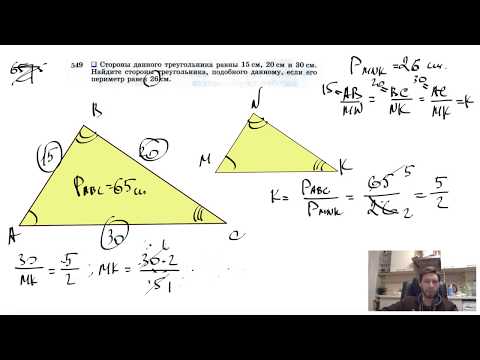
Видео:№549. Стороны данного треугольника равны 15 см, 20 см и 30 см. Найдите стороны треугольникаСкачать
Тест по теме «Признаки равенства треугольников»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
тест по теме: «признаки равенства треугольников»
1. Для доказательства равенства треугольников АВС и NКМ достаточно доказать, что…
1) 
С = К;
2) С = М;
3) В = М.
2. Для доказательства равенства треугольников АPK и DCE достаточно доказать, что…
3. Из равенства треугольников АВК и MNF следует, что…
1) В = М;
2) В = N;
3) В = F.
4. Чтобы доказать равенство двух равнобедренных треугольников, недостаточно доказать равенство…
1) углов при основаниях;
2) оснований и углов при основаниях;
3) оснований и углов при вершине.
1) если сумма двух сторон и периметр одного треугольника соответственно равны сумме двух сторон и периметру другого треугольника, то такие треугольники равны;
2) если сумма двух сторон и угол между ними одного треугольника соответственно равны сумме двух сторон и углу между ними другого треугольника, то такие треугольники равны;
3) если две стороны и периметр одного треугольника соответственно равны двум сторонам и периметру другого треугольника, то такие треугольники равны.
1) АВ = А1В1, ВС = В1С1, А = А1;
2) АС = А1С1, ВС = В1С1, С = С1;
3) А = А1, В = В1, С = С1.
7. В треугольниках АВС и MKN АВ = MK, ВС = NK, В = K.
В треугольниках проведены медианы (см. рис.).
8. Для данного четырехугольника неверно, что…
3) А = С.
9. Для данного четырехугольника верно, что…
1. ∆ МКР = ∆ М1К1Р1, М = М1, К1Р1 = 5 см.
2. ∆ АВС = ∆ MFK, В = М.
Тогда разность АС – FK равна…
3. Отрезки KP и EF пересекаются в точке М так, что KM = MP и EM = MF. PF = 12 см.
4. Медиана АМ треугольника АВС перпендикулярна стороне ВС.
ВАС = 40°.
Тогда ВАМ = …
5. В четырехугольнике АВСD 1 = 2, 3 = 4. ВD = 5 см.
Периметр четырехугольника равен 32 см. Тогда периметр треугольника АВD равен…
6. Точка О делит пополам диагональ…
тест по теме: «признаки равенства треугольников»
1. Для доказательства равенства треугольников АВС и КМР достаточно доказать, что…
2. Для доказательства равенства треугольников АВС и РEК достаточно доказать, что…
1) 
С = Е;
2) С = К;
3) С = Р.
3. Из равенства треугольников АРК и MFN следует, что…
3) A = M.
4. Чтобы доказать равенство двух равнобедренных треугольников, достаточно доказать равенство…
2) боковых сторон;
3) оснований и боковых сторон.
5. Какое высказывание неверное?
1) Если периметры равносторонних треугольников равны, то равны и треугольники.
2) Если периметры равнобедренных треугольников равны, то равны и треугольники.
3) Периметры равных равнобедренных треугольников равны.
1) АС = А1С1, В = В1, С = С1;
2) АВ = А1В1, АС = А1С1, С = С1;
3) А = А1, В = В1, С = С1.
7. В треугольниках АВС и MNP MP = AC, M = A, P = C.
В треугольниках проведены биссектрисы (см. рис.).
8. Для данного четырехугольника неверно, что…
3) В = D.
9. Для данного четырехугольника верно, что…
3) А = С.
1. ∆ АВС = ∆ А1В1С1, ВС = В1С1, A = 35°.
Тогда A1 = …
2. ∆ АВС = ∆ MFK, А = М.
Тогда отношение 
равно…
3. Отрезки AD и BC пересекаются в точке О так, что АО = OD и СО = ОВ.
CDO = 34°. Тогда ВАО = …
4. Биссектриса AD треугольника АВС перпендикулярна стороне ВС. ВС = 7,2 см.
5. В четырехугольнике MNPQ 1 = 2, 3 = 4. NQ = 9 см.
Периметр четырехугольника равен 28 см. Тогда периметр треугольника MNQ равен…
Видео:№10. Верно ли, что прямая лежит в плоскости данного треугольника, если онаСкачать
Неравенство треугольника — определение и вычисление с примерами решения
Содержание:
Неравенство треугольника:
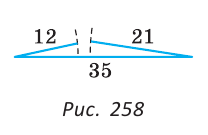
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).
Замечание. Из неравенств треугольника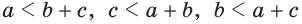 
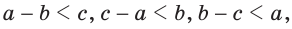
следует, что 
то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо 
Пример:
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.
Решение:
Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС 
B (рис. 108, а).
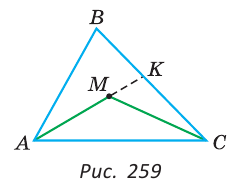
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).
3) Так как АF 1.
4) Угол 2 является внешним углом треугольника ВFС, следовательно, 2 > B.
5) Так как треугольник FАС является равнобедренным, то 1 = 2.
Таким образом, BСА > 1, 1 = 2 и 2 > B.
Отсюда получаем, что ВСА > B.
Теорема 2. В треугольнике против большего угла лежит большая сторона.
1) Пусть в треугольнике АBС С > B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.
2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ C.
В каждом из этих случаев получаем противоречие с условием: C > B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.
Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.
Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.
Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.
Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.
Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.
Неравенство треугольника
Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.
Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.
1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ l, следовательно, верно неравенство АВF > 2.
4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎦 Видео
№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать
Площадь треугольника. Как найти площадь треугольника?Скачать
Неравенства треугольника. Практическая часть. 7 класс.Скачать
Геометрия 7 класс (Урок№9 - Треугольник.)Скачать
Неравенство треугольника. Геометрия 7 класс. Доказательство. Задачи по рисункам.Скачать
Треугольники. 7 класс.Скачать
№584. Все стороны треугольника ABC касаются сферы радиуса 5 см. Найдите расстояние от центра сферыСкачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать
8 класс, 25 урок, Средняя линия треугольникаСкачать
Построение треугольника, равного данномуСкачать
28012014 Неравенства треугольникаСкачать
❓ Неизвестное устройство в Windows. Как решить проблему?Скачать
7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать
Не хочу своего мужа! / Страсть и зависимость / Как выйти из любовного треугольника / НевернаяСкачать
7 класс, 14 урок, ТреугольникСкачать
Равные треугольники. Высота, медиана, биссектриса треугольника - геометрия 7 классСкачать
Мужчина проснулся на дне колодца, но когда вылез еще больше разочаровалсяСкачать
