Материальная точка движется равнозамедленно по окружности определить направление углового ускорения

В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.

Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.

За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек — сложно.

Видео:Физика - движение по окружностиСкачать

Угловое перемещение

Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Угловая скорость и угловое ускорение

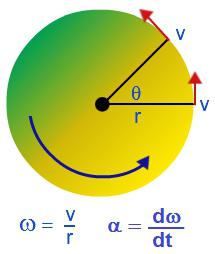
Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.

Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.

Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.

Вращательное движение тела характеризуется еще одной физической величиной — угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с 2 .

Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Равномерное вращательное движение

Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ₀ + ωt, где φ₀ – начальное значение угла поворота.

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Равноускоренное вращательное движение

Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω₀+ εt, φ = φ₀ + ω₀t + εt 2 /2.

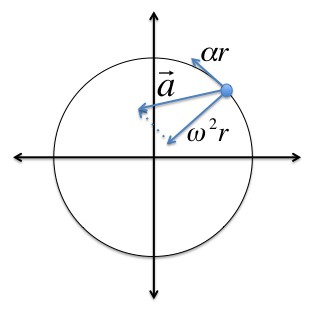
Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑ_ц = v 2 /R = (ωR) 2 /R = ω 2 R.

Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑ_t = ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Момент сил

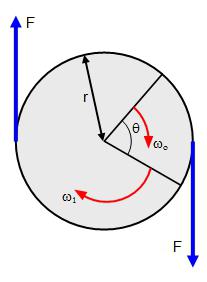
Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.

Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α — угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M₁ + M₂ + …+ M_n.

Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R 2 mβ, β= M/mR 2 = M/I, где I = mR 2 — момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.

Видео:Вращательное движение. 10 класс.Скачать

Примеры решения задач

Задача 1. Ротор центрифуги делает 2•10 4 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.

Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω₀ — εt.

Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω₀/t = 2πn/t.

Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с 2 ).

Угол поворота ротора центрифуги за время t будет: φ(t)= φ₀ + ω₀t + εt 2 /2. Учитывая выражение для углового ускорения и то, что φ₀ = 0, находим: φ(t)= ω₀t/2 = πnt.

Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10 4 (об.).

Ответ: угловое ускорение равно 4,36 рад/с 2 ; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10 4 об.

Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.

Найдем тормозной момент сил, действующий на диск: M = RF.

Найдем угловое ускорение диска: ε = M/I = FR/mR 2 = F/mR.

Найдем время, за которое диск остановится: t = ω₀/ε, где ω₀ — начальная угловая скорость диска, которая равна 2πv.

Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).

Ответ: время остановки равно 2,5 с.

Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Виды движения по окружности

Угловое движение можно условно разделить на два вида:

1. Когда изменяется только направление вектора линейной скорости, а его длина не изменяется.
2. Или, когда изменяются обе характеристики вектора линейной скорости.

Во втором случае, для описания движения будем применять более сложные формулы кинематики. Так как появится еще один вид ускорения.

Центростремительное (нормальное) ускорение есть всегда, когда есть движение по окружности, при этом не важно, меняется ли скорость тела по модулю, или не меняется.

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Движение по окружности с постоянной по модулю скоростью

Пусть тело движется по окружности, но при этом длина вектора линейной скорости не меняется (рис. 1).

[left|vec right| = const]

На рисунке 1 указаны: а) – вид сбоку, б) вид сверху, вектор угловой скорости направлен к нам перпендикулярно рисунку.

Скорость будет меняться только по направлению от точки к точке, потому, что на тело действует центростремительная сила (displaystyle vec<F_<text>>) , тело обладает центростремительным (displaystyle vec<a_<text>>) (нормальным) ускорением.

Кроме линейной, тело обладает угловой скоростью. Если линейная скорость не изменяется по модулю, то длина вектора угловой скорости не меняется.

На рисунке 1а изображен вектор угловой скорости (displaystyle vec), на рисунке 1б вектор угловой скорости направлен к нам перпендикулярно плоскости рисунка. Направление, в котором тело движется по окружности, указано синей стрелкой.

Видео:Центростремительное ускорение. 9 класс.Скачать

Тангенциальное ускорение – когда модуль скорости меняется

Тело может увеличивать или уменьшать свою скорость, когда движется по окружности.

В таком случае, дополнительно к нормальному ускорению возникает тангенциальное (displaystyle vec<a_>) ускорение.

Тангенциальное ускорение играет роль линейного ускорения при прямолинейном движении тела. Вектор (displaystyle vec<a_>) направлен параллельно вектору (displaystyle vec) скорости.

Подобно движению по прямой, вектор ускорения – это первая производная скорости по времени, или вторая производная перемещения по времени.

Когда векторы скорости (vec) и ускорения (vec<a_>) сонаправлены (рис. 2), линейная и угловая скорости возрастают.

А когда ускорение (vec<a_>) направлено противоположно (рис. 3) вектору скорости (vec), угловая и линейная скорости уменьшаются.

С линейной скоростью (vec) связана угловая (vec) скорость.

Из рисунков 2, 3 следует: когда появляется тангенциальное ускорение, меняется и угловая скорость. Значит, тангенциальное ускорение (vec<a_>) появляется совместно с угловым (vec) ускорением и между ними есть связь.

Связь между тангенциальным и угловым ускорением выглядит аналогично связи между линейной и угловой скоростью.

В векторном виде

В скалярном виде

[ large boxed < a_= beta cdot R >]

(displaystyle vec left( frac<text><c^>right)) – угловое ускорение;

(displaystyle vec< a_> left( frac<text><c^>right)) – тангенциальное ускорение;

(R left( textright)) – радиус окружности.

Видео:3. Кинематика материальной точки. Угловые величиныСкачать

Равноускоренное движение по окружности

Угловая скорость увеличивается (рис. 2), когда угловое ускорение сонаправлено с вектором угловой скорости. Когда движение происходит с постоянным ускорением, его называют равноускоренным.

Для решения задач на равноускоренное движение по окружности, поступаем аналогично равноускоренному движению по прямой. Применяем систему из двух уравнений:

[ large boxed < beginomega = omega _ + beta cdot t \ displaystyle varphi = omega_ cdot t + beta cdot frac end > ]

Первое уравнение системы – это связь между начальной (omega_ ) и конечной (omega ) скоростью. Второе уравнение – это уравнение движения.

Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Равнозамедленное движение по окружности

Когда векторы (vec) и (vec) направлены в противоположные стороны, угловая скорость (vec) уменьшается (рис. 3).

Для решения задач кинематики, в которых угловая скорость уменьшается и, движение равнозамедленное, используем систему, состоящую из таких уравнений:

[ large boxed < beginomega = omega _ — beta cdot t \ displaystyle varphi = omega_ cdot t — beta cdot frac end > ]

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Общее ускорение при движении по окружности

Пусть точка движется по окружности и линейная (vec) скорость ее изменяется по модулю. При этом, точка обладает двумя видами ускорения — нормальным и тангенциальным. Эти виды ускорения обозначают символом (vec).

Примечание: Любое ускорение, обозначаемое символом «a», измеряется в метрах, деленных на секунду в квадрате.

Направление вектора общего ускорения указано на рисунке 4а, а для равнозамедленного – на рисунке 4б.

Так как векторы (vec<a_>) и (vec<a_>) всегда перпендикулярны, длину вектора общего ускорения (vec) можно найти из теоремы Пифагора:

Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Материальная точка движется равнозамедленно по окружности определить направление углового ускорения

тангенциальное нормальное полное ускорения

Колесо с радиусом 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ = 5+t+2t 2 +t 3 рад. Для точек, лежащих на ободе колеса, определить угловую скорость, угловое, нормальное, тангенциальное и полное ускорения к концу второй секунды. Какой угол образует вектор полного ускорения и вектор линейной скорости?

Материальная точка движется по окружности радиуса 1 м согласно уравнению s = 8t – 0,2t 3 . Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.

Колесо радиусом 0,3 м вращается согласно уравнению φ = 5–2t+0,3t 2 . Найти нормальное, тангенциальное и полное ускорение точек на ободе колеса через 5 с после начала движения.

Шарик массы т = 100 г, подвешенный на нити, отвели в сторону так, что нить образовала прямой угол с вертикалью, а затем отпустили. Найти: 1) тангенциальное, нормальное и полное ускорение и натяжение нити в зависимости от угла θ отклонения нити от вертикали; 2) натяжение нити в тот момент, когда вертикальная составляющая скорости шарика максимальна.

Используя данные предыдущей задачи, определить: 1) частоту вращения диска в момент времени t₂ в об/с и об/мин; 2) в момент времени t₂ определить скорость, нормальное, тангенциальное и полное ускорение точек, находящихся на расстоянии 10 см от оси вращения.
Данные из предыдущей задачи: t₂ = 15 с; ω(t₂) = 11,8 рад/с; β(t₂) = 1,1 рад/с 2 .
Предыдущая задача: Диск вращается согласно уравнению φ = а + bt + ct 2 + dt 3 , где φ — угол поворота радиуса в радианах, t — время в секундах. Определить угловую скорость и ускорение в моменты времени t₁ = 11 с и t₂ = 15 с. Каковы средние значения угловой скорости и углового ускорения в промежутке времени от t₁ = 11 до t₂ = 15 с включительно, если для Вашего варианта а = 1, b = 2 с –1 , с = 0,1 с –2 , d = 0,01 с –3 ?

Точка движется по кругу так, что зависимость пути от времени задается уравнением: S = А + Bt +Ct 2 , где В = –2 м/с и С = 1 м/с 2 . Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через 3 с после начала движения, если известно, что нормальное ускорение в момент времени 2 с составляет 0,5 м/с 2 .

Найти нормальное, тангенциальное и полное ускорение электрона на произвольной стационарной орбите в ионе Не+.

Движение точки по окружности радиуса R = 4 м задано уравнением: S = A+Bt+Ct 2 . Определить тангенциальное, нормальное и полное ускорение точки в момент времени t = 2 с, если А = 10 м, В = –2 м/с и С = 1 м/с 2 .

Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Длина пути автомобиля выражается уравнением S = 10+10t+0,5t 2 (путь — в метрах, время — в секундах). Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорения через 5 с после начала движения.

Материальная точка движется по окружности радиуса 80 см по закону S = 10t–0,1t 3 (путь в метрах, время в секундах). Найти скорость, тангенциальное, нормальное и полное ускорения через 2 с после начала движения.

Материальная точка движется по окружности диаметром 40 м. Зависимость ее координаты от времени движения определяется уравнением S = t 3 +4t 2 –3t+8. В какой момент точка изменяет направление движения? Определить пройденный путь, скорость, нормальное, тангенциальное и полное ускорение движущейся точки через 4 с после начала движения.

Тело движется по криволинейной траектории. Пройденный путь меняется со временем по закону s = 2 + 0,5t 2 , м. Определить нормальное, тангенциальное и полное ускорение при t = 1 с. Радиус кривизны траектории движения в этот момент времени равен 50 см. Какова средняя скорость за 1 с движения?

Материальная точка начала вращаться с постоянным угловым ускорением из положения 1 и через 0,1 с оказалась в положении 2. Найти угловые ускорение и скорость в точке 2. Указать направления тангенциального, нормального и полного ускорений, а также линейной и угловой скоростей для положения 2.

Движение точки по окружности радиусом R = 2 м задано уравнением φ = A+Bt+Ct 2 , где А = 10 м, В = –3 м/с, С = 2 м/с 2 . Найти тангенциальное, нормальное и полное ускорения точки в момент времени t = 2 с.

🎬 Видео

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Лекция 10. Угловая скорость и угловое ускорение │Физика с нуляСкачать

угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать

РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Физика | Равномерное движение по окружностиСкачать