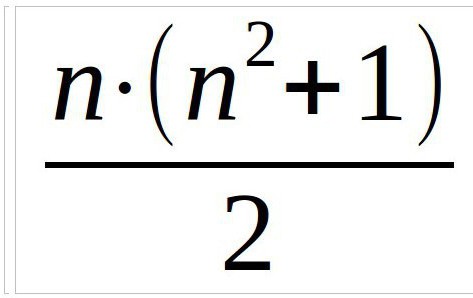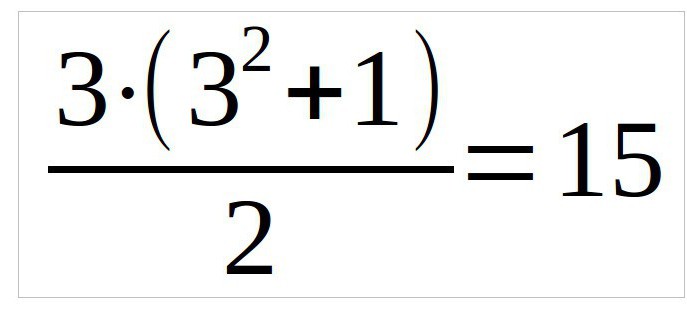Магические треугольники и квадраты

Разделы: Математика

В повышении эффективности и качества учебного процесса в младших классах важным условием является развитие логического мышления, умение решать текстовые задачи, формирование отвлеченных теоретических знаний младших школьников.

Роль задач в обучении математике невозможно переоценить.

Разрешив систему специально подобранных задач, ученик знакомится с существенными элементами новых алгоритмов, овладевает новыми техническими элементами. Применять математические знания в жизненных ситуациях учат соответствующие практические задачи.

Получив задачу нужно разобраться в том, что это за задача, каковы ее условия, в чем состоят ее требования. Надо провести анализ задачи это и составляет первый этап процесса решения задачи. (Приложение 1, слайд 2) В ряде случаев этот анализ надо оформить, записать. Для этого используются разного рода схематические записи задач, построение которых составляет второй этап процесса решения. Анализ задачи и построение ее схематической записи необходимо главным образом для того, чтобы найти способ решения данной задачи. Поиск этого способа составляет третий этап процесса решения.

Когда способ решения задачи найден, его нужно осуществлять, это будет четвертый этап осуществления решения.

После того как решение осуществлено и изложено, необходимо убедиться что это решение правильное, что оно удовлетворяет всем требованиям задачи. Для этого производят проверку решения, что составляет пятый этап процесса решения.

При решении многих задач, кроме проверки, необходимо еще произвести исследование задачи, а именно установить, при каких условиях задача имеет решение и притом сколько различных решений в каждом отдельном случае; при каких условиях задача вообще не имеет решения. Это составляет шестой этап процесса решения. Убедившись в правильности решения и если нужно произведя исследование задачи необходимо четко сформулировать ответ задачи это будет седьмой этап процесса решения.

В учебных и познавательных целях полезно также произвести анализ выполненного решения, в частности установить, нет ли другого, более рационального способа решения. Все это составляет восьмой этап решения.

Итак, весь процесс решения задачи можно разделить на восемь этапов.

Приведенная схема дает общее представление о процессе решения задач. (Приложение 1, слайд 3)

Наибольшее затруднения у школьников вызывают решения нестандартных задач, т.е. задач, алгоритм решения которых им неизвестен.

В основе решений многих из них лежит: принцип Дирихле, понятие инварианта, запись чисел в различных системах счисления, теория графов, свойства геометрических и математических фигур, признаки делимости чисел, правила комбинаторики и т.д.

Принцип Дирихле. Это простое положение применяется при доказательстве многих важных теорем теории чисел. (Приложение 1, слайд 4)

Пример. В мешке лежат шарики двух разных цветов: черного и белого. Какое наименьшее число шариков нужно вынуть из мешка вслепую так, чтобы среди них оказались два шарика одного цвета?

Решение. Достанем из мешка три шарика. Если бы среди этих шариков было не более одного шарика каждого из двух цветов, то всего было бы не более двух шаров – это очевидно и противоречит тому, что мы достали три шарика.С другой стороны, ясно, что двух шариков может и не хватить.В этой задаче «кроликами» являются шарики, а «клетками» – цвета: белый и черный.

ИНВАРИАНТ. Главная идея применения инварианта заключается в следующем. Берутся некие объекты, над которыми разрешено выполнять определенные операции, и задается вопрос: «Можно ли из одного объекта получить другой при помощи этих операций?». Чтобы ответить на него, строят некоторую величину, которая не меняется при указанных операциях. Если значения этой величины для двух указанных объектов не равны, то ответ на заданный вопрос отрицателен.

Пример. На доске написано 11 чисел – 6 нулей и 5 единиц. Предлагается 10 раз подряд выполнить такую операцию: зачеркнуть любые два числа и, если они были одинаковы, дописать к оставшимся числам один ноль, а если разные – единицу. Какое число останется на доске?

Решение. Нетрудно заметить, что после каждой операции сумма всех чисел на доске остается не четной, какой она и была вначале. Действительно, сумма каждый раз меняется на 0 или 2. Значит, и после 10 операций оставшееся число должно быть нечетным, т.е. равным 1.

В этом примере инвариант — это четность суммы написанных чисел.

Главное в решении задач на инвариант – придумать сам инвариант.

МАГИЧЕСКИЕ ФИГУРЫ. Этот вид головоломок мы можем встретить на страницах многих учебников математики. Магические фигуры делятся на плоские и пространственные, так как существуют магические квадраты, треугольники, прямоугольники, многоугольники и круги, а также и магические кубы.

Отметим основные свойства магических квадратов.

Свойство 1. Магический квадрат останется магическим, если все числа, входящие в его состав, увеличить или уменьшить на одно и то же число.

Свойство 2. Магический квадрат останется магическим, если умножить или разделить все его числа на одно и то же число.

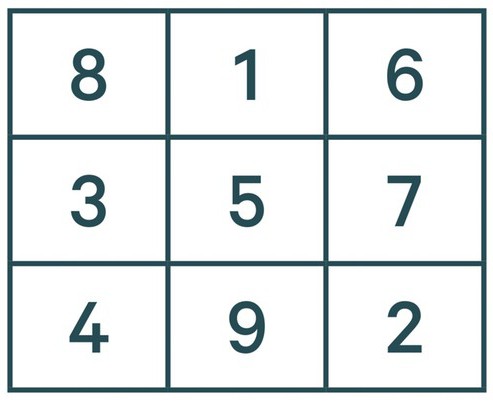
Пример. В квадрате на рис. 1а магическая сумма равна 15; квадрат на рис. 1б получается из него прибавлением 17 к каждому числу, его волшебная сумма равна 15 + 3 * 17 = 66; умножив все числа в новом квадрате на 2, получим еще один квадрат (рис. 1в), магическая сумма которого равна 2 * 66 = 132.

Свойство 3.Если квадрат является магическим для какой-нибудь арифметической прогрессии, то он будет магическим для так же расположенной арифметической прогрессии с другим первым членом и с другой разностью.

Правило. Составляя какой-либо магический квадрат, достаточно сначала составить его из простейших чисел, т.е. из чисел натурального ряда: 1, 2, 3, 4, 5. а затем путем умножения, деления, увеличения или же уменьшения этих чисел можно получить бесконечное число магических квадратов с самыми разнообразными магическими суммами.

Свойство 4. Из двух магических квадратов можно получить третий, складывая числа, расположенные в соответствующих полях. Магическая сумма такого квадрата равна сумме магических сумм обоих слагаемых: 81 = 15 + 66 (см. рис. 2).

Свойство 5. Квадрат не утратит своих магических свойств, если переставить его столбцы и ряды, расположенные симметрично относительно центра квадрата.

Построение нечетных магических квадратов. Существует очень много различных методов построения магических квадратов:

• индийский метод (Приложение 1, слайд 8)
• сиамский метод, метод Баше (Приложение 1, слайд 9)
• треугольники с магическим периметром (Приложение 1, слайды 10-11)
• магические круги (Приложение 1, слайд 12)

Задачи в «математическую копилку учителя»

13. Постройте магический квадрат 3 х 3, в котором расположите числа от 3 до 11 так, чтобы по всем строкам, столбцам и диагоналям была одна и та же сумма.

14. В квадрате 4 x 4 расставьте четыре одинаковых буквы так, чтобы в каждом горизонтальном ряду, в каждом вертикальном ряду и в каждой диагонали встречалась только одна буква.

15. В квадрате 4 x 4 расставьте 16 букв (четыре буквы а, четыре Ь, четыре с, четыре d) так, чтобы в каждом горизонтальном ряду и в каждом вертикальном ряду буква встречалась только один раз, т.е. постройте так называемый латинский квадрат размером 4 x 4.

16. Переставьте числа в треугольнике, показанном на рис. 3 так, чтобы сумма чисел в каждом треугольнике (по 4 ячейки) стала равна 23, а в каждой трапеции (по 5 ячеек) – 22.

17. Задача Эйнштейна. Девять кругов расположены так, как показано на рис. 3а. Расположите в них числа от 1 до 9 так, чтобы сумма чисел, лежащих в вершинах каждого из семи изображенных на рисунке треугольников, была одна и та же.

Ответ показан на рис. 3б.

18. Заполните числами кружки так, чтобы сумма чисел в каждом ряду была равна 38 (рис. 4а).

Ответ показан на рис. 46.

Математические олимпиады являются одной из форм внеклассной работы и массовых соревнований учащихся. Работа по подготовке к олимпиадам должна вестись системно, не только за месяц до начала олимпиад, а постоянно на каждом уроке.

Начиная с 1 класса в начале каждого урока можно включать в устный счет хотя бы одну задачу, требующую нестандартного подхода при своем решении. В младших классах это может быть задача со сказочным сюжетом, с нестандартными вычислениями, но требующие умения размышлять, анализировать задания, направленные на развитие сообразительности и логического мышления. Можно назвать этот этап урока «Утренней сказкой» или «Разминкой».

У учащихся подобные приемы работы формируют интерес к математике, развивают логическое мышление. Решение таких задач можно поощрять, например: ученик, решивший первым задачу, получает 1 балл, который может добавить к любой полученной на уроке оценке. Обычно этот этап урока учащимся очень нравится, и они активно включаются в решение подобных задач.

Учителю эта работа позволяет уже на раннем этапе, в 5-6 классах выявить нестандартно мыслящих, сообразительных детей из которых в будущем можно собрать команду олимпийцев.

Переходя в среднее звено, эти дети уже имеют более широкие возможности для развития своих способностей. Когда сформирована группа наиболее продвинутых учащихся, с ними уже можно работать отдельно. Здесь приемлемы такие общепринятые методы, как кружковые, индивидуальные.

Вместе с тем работу по подготовке к олимпиаде вести активно и на уроке. Ведь некоторые задачи повышенной сложности – задачи нестандартного характера являются приемом продолжения изучаемого программного материала, и поэтому целесообразно решать их в ходе изучения соответствующей темы. Я подобрала тексты нестандартных задач и способы их решения, которые может использовать в работе любой учитель.

Таким образом, математические олимпиады способствуют развитию таких ценных качеств личности, как настойчивость, целеустремленность, самостоятельность и трудолюбие, вырабатывает навыки научно-исследовательского характера.

Видео:Магические квадраты – тысячи лет восхищения // Vital MathСкачать

Магический квадрат — виды, правила и примеры решения

Среди поклонников логических игр большой популярностью пользуется магический квадрат. Он представляет собой таблицу, заполненную особым образом цифрами. Причём сумма чисел одинакова по всем направлениям. Эту величину принято называть константой. Существует множество вариантов таких головоломок разной степени сложности.

Видео:Как решать магический квадратСкачать

История и современное применение

Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.

В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.

С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.

Видео:Магические квадратыСкачать

Квадрат нечётного порядка

Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.

Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:

Оставшуюся клетку занимает девятка.

Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.

Видео:Magic cube **72 shapes** How to assemble all the molds?/Магический куб **72 фигуры** Как собрать?Скачать

Одинарная чётность

Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.

Вычисление магической константы

Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.

Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.

Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.

Дальнейшие действия

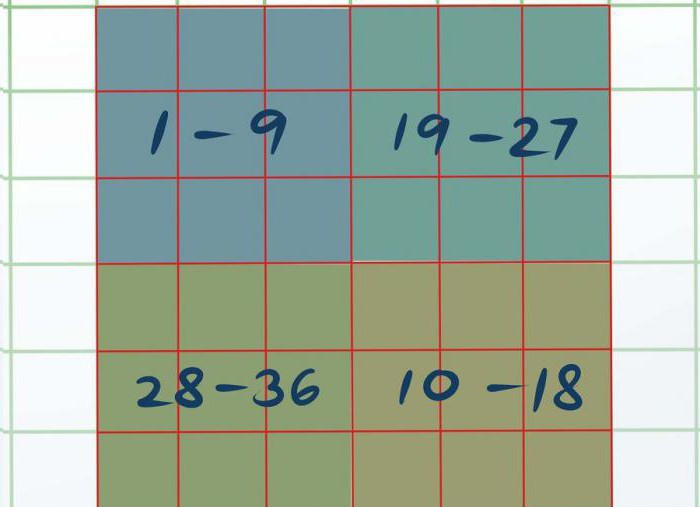
Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.

Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:

Далее переходят в квадрант D и формируют обособленную область D.

Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.

Видео:🔥 ФОКУС с треугольником #shortsСкачать

Двойной порядок

Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.

Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:

В четвёртой строке слева пишется 13, а справа — 16.

По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.

Видео:Как это решить?Скачать

Как решить магический квадрат (3 класс)? Пособия для школьников

Математических загадок существует невообразимое количество. Каждые из них уникальны по-своему, но их прелесть заключается в том, что для решения неизбежно нужно приходить к формулам. Конечно же, можно попытаться решить их, как говорится, методом тыка, но это будет очень долго и практически безуспешно.

В данной статье будет говориться об одной из таких загадок, а чтобы быть точнее — о магическом квадрате. Мы детально разберем, как решить магический квадрат. 3 класс общеобразовательной программы, конечно, это проходит, но возможно не каждый понял или вовсе не помнит.

Видео:МАГИЧЕСКИЕ КВАДРАТЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Что это за загадка?

Магический квадрат, или, как его еще называют, волшебный, — это таблица, в которой число столбцов и строк одинаково, и все они заполнены разными цифрами. Главная задача, чтобы эти цифры в сумме по вертикали, горизонтали и диагонали давали одинаковое значение.

Помимо магического квадрата, есть еще и полумагический. Он подразумевает то, что сумма чисел одинакова лишь по вертикали и горизонтали. Магический квадрат «нормальный» только в том случае, если для заполнения использовались натуральные числа от единицы.

Еще есть такое понятие, как симметричный магический квадрат — это когда значение суммы двух цифр равно, в то время, когда они располагаются симметрично по отношению к центру.

Важно также знать, что квадраты могут быть любой величины помимо 2 на 2. Квадрат 1 на 1 также считается магическим, так как все условия выполняются, хотя и состоит он из одного-единственного числа.

Итак, с определением мы ознакомились, теперь поговорим про то, как решить магический квадрат. 3 класс школьной программы вряд ли все так детально разъяснит, как эта статья.

Видео:Магические квадраты от моего Папы!Скачать

Какие есть решения

Те люди, которые знают, как решить магический квадрат (3 класс точно знает), сразу же скажут, что решения только три, и каждое из них подходит для разных квадратов, но все же нельзя обойти стороной и четвертое решение, а именно «наугад». Ведь в какой-то мере есть вероятность того, что незнающий человек все же сможет решить данную задачку. Но данный способ мы отбросим в длинный ящик и перейдем непосредственно к формулам и методикам.

Видео:Великая скрытая сила и мощь треугольника - Садхгуру на РусскомСкачать

Первый способ. Когда квадрат нечетный

Данный способ подходит только для решения такого квадрата, у которого количество ячеек нечетное, например, 3 на 3 или 5 на 5.

Итак, в любом случае изначально необходимо найти магическую константу. Это число, которое получится при сумме цифр по диагонали, вертикали и горизонтали. Вычисляется она с помощью формулы:

В данном примере мы рассмотрим квадрат три на три, поэтому формула будет выглядеть так (n — число столбцов):

Итак, перед нами квадрат. Первое, что надо сделать — это вписать цифру один в центре первой строки сверху. Все последующие цифры необходимо располагать на одну клетку правей по диагонали.

Но тут сразу встает вопрос, как решить магический квадрат? 3 класс вряд ли использовал данный метод, да и у большинства появится проблема, как это сделать таким способом, если данной клетки нет? Чтобы сделать все правильно, необходимо включить воображение и дорисовать аналогичный магический квадрат сверху и получится так, что число 2 будет находиться в нем в нижней правой клетке. Значит, и в наш квадрат мы вписываем двойку в то же место. Это означает, что нам необходимо вписать цифры так, чтобы в сумме они давали значение 15.

Последующие цифры вписываются точно так же. То есть 3 будет находиться в центре первого столбца. А вот 4 по такому принципу вписать не удастся, так как на ее месте уже стоит единица. В таком случае цифру 4 располагаем под 3, и продолжаем. Пятерка — в центре квадрата, 6 — в правом верхнем углу, 7 — под 6, 8 — в верхний левый и 9 — по центру нижней строки.

Вы теперь знаете, как решить магический квадрат. 3 класс Демидова проходил, но у этого автора были чуть попроще задания, однако, зная данный способ, удастся разгадать любую подобную задачу. Но это, если число столбцов нечетное. А что же делать, если у нас, например, квадрат 4 на 4? Об этом дальше по тексту.

Видео:ПОЧЕМУ НЕЛЬЗЯ ЗАХОДИТЬ В КРАСНЫЙ КВАДРАТ ЭТОГО ЖИТЕЛЯ В МАЙНКРАФТ | Компот MinecraftСкачать

Второй способ. Для квадрата двойной четности

Квадратом двойной четности называют тот, у которого количество столбцов можно разделить и на 2, и на 4. Сейчас мы рассмотри квадрат 4 на 4.

Итак, как решить магический квадрат (3 класс, Демидова, Козлова, Тонких — задание в учебнике математики), когда количество его столбцов равно 4? А очень просто. Проще, чем в примере до этого.

В первую очередь находим магическую константу по той же формуле, что приводилась в прошлый раз. В данном примере число равно 34. Теперь надо выстроить цифры так, чтобы сумма по вертикали, горизонтали и диагонали была одинаковой.

В первую очередь надо закрасить некоторые ячейки, сделать это вы можете карандашом или же в воображении. Закрашиваем все углы, то есть верхнюю левую клеточку и верхнюю правую, нижнюю левую и нижнюю правую. Если квадрат был бы 8 на 8, то закрашивать надо не одну клеточку в углу, а четыре, размером 2 на 2.

Теперь необходимо закрасить центр этого квадрата, так, чтобы его углы касались углов уже закрашенных клеточек. В данном примере у нас получится квадрат по центру 2 на 2.

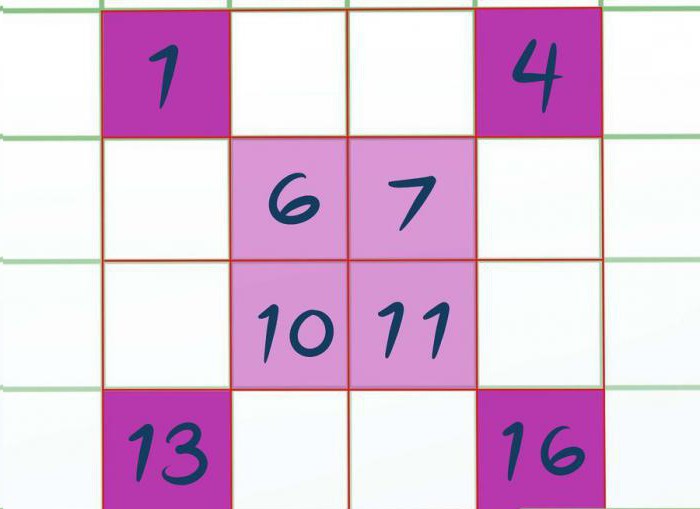
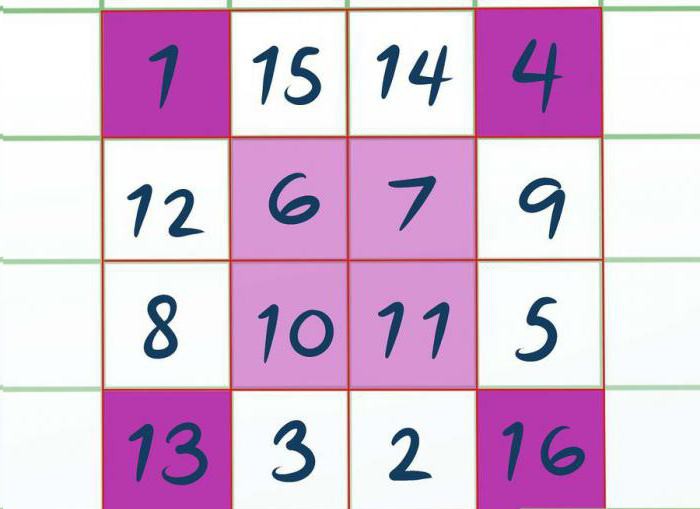
Приступаем к заполнению. Заполнять будем слева направо, в том порядке, в котором расположены ячейки, только вписывать значение будем в закрашенные клетки. Получается, что в верхний левый угол вписываем 1, в правый — 4. Потом центральный заполняем 6, 7 и дальше 10, 11. Нижний левый 13 и правый — 16. Думаем, порядок заполнения понятен.

Остальные ячейки заполняем точно так же, только в порядке убывания. То есть так как последняя вписанная цифра была 16, то вверху квадрата пишем 15. Далее 14. Потом 12, 9 и так далее, как показано на картинке.

Теперь вы знаете второй способ, как решить магический квадрат. 3 класс согласится, что квадрат двойной четности намного легче решается, чем другие. Ну а мы переходим к последнему способу.

Видео:Мы построили двухэтажную кровать в чемодане! Хорошая vs плохая мамаСкачать

Третий способ. Для квадрата одинарной четности

Квадратом одинарной четности называется, тот квадрат, число столбцов которого можно разделить на два, но нельзя на четыре. В данном случае это квадрат 6 на 6.

Итак, вычисляем магическую константу. Она равна 111.

Теперь нужно наш квадрат визуально поделить на четыре разных квадрата 3 на 3. Получится четыре маленьких квадрата размером 3 на 3 в одном большом 6 на 6. Верхний левый назовем А, нижний правый — В, верхний правый — С и нижний левый — D.

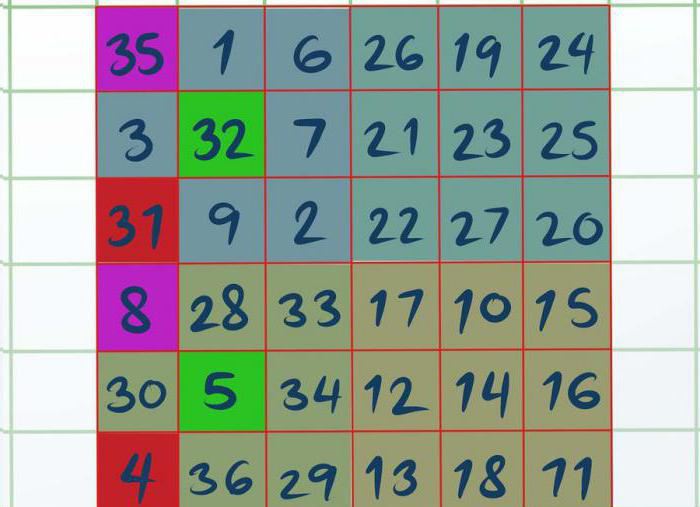
Теперь необходимо каждый маленький квадрат решить, используя самый первый способ, что приведен в этой статье. Получится так, что в квадрате А будут числа от 1 до 9, в В — от 10 до 18, в С — от 19 до 27 и D — от 28 до 36.

Как только вы решили все четыре квадрата, работа начнется над А и D. Необходимо в квадрате А визуально или при помощи карандаша выделить три ячейки, а именно: верхнюю левую, центральную и нижнюю левую. Получится так, что выделенные цифры — это 8, 5 и 4. Точно так же надо выделить и квадрат D (35, 33, 31). Все, что остается сделать, это поменять местами выделенные цифры из квадрата D в А.

Теперь вы знаете последний способ, как можно решить магический квадрат. 3 класс квадрат одинарной четности не любит больше всего. И это неудивительно, из всех представленных он самый сложный.

Видео:Магические квадратыСкачать

Вывод

Прочтя данную статью, вы узнали, как решить магический квадрат. 3 класс (Моро — автор учебника) предлагает подобные задачи только с несколькими заполненными ячейками. Рассматривать его примеры нет смысла, так как зная все три способа, вы с легкостью решите и все предлагаемые задачи.

📽️ Видео

Как решать магические квадратыСкачать

Как сложить доллар треугольником. Магия денег. Привлекаем деньги. Видео ютуб. Канал ТУТСИ.Скачать

Решите задачу про магический квадрат за 1 минуту. Сможете?Скачать

Магический квадрат. Угадай какие числа пропущены?Скачать

Учимся решать "Магический квадрат"Скачать

24 Часа в ЛИФТЕ !Скачать

Магические квадраты. Урок 129. Математика 2 классСкачать

Треугольник в квадрате Magical Triangle - Think Outside The Box!Скачать