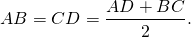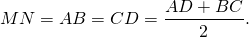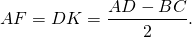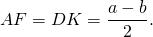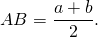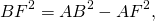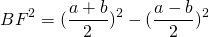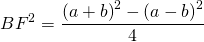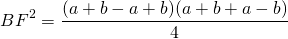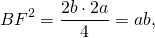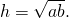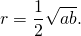Укажите номера верных утверждений.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «В любую равнобедренную трапецию можно вписать окружность.» — неверно, не в любую равнобедренную трапецию можно вписать окружность.
2) «Диагональ параллелограмма делит его углы пополам.» — неверно, диагональ параллелограмма делит его углы пополам только в том случае, когда параллелограмм является ромбом.
3) «Площадь прямоугольного треугольника равна половине произведения его катетов.» — верно, это теорема планиметрии.
Аналоги к заданию № 311763: 311915 311959 Все
Видео:Окружность, вписанная в трапециюСкачать
Любую равнобедренную трапецию можно вписать окружность верно
Какие из следующих утверждений верны? Запишите их номера без пробелов и других дополнительных символов в порядке возрастания.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов
1) В любую равнобедренную трапецию можно вписать окружность — неверно. Так как в трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
2) Диагональ параллелограмма делит его углы пополам — неверно. Так как для этого требуется условие равенства всех сторон параллелограмма.
3) Площадь прямоугольного треугольника равна половине произведения его катетов — верно.
Ответ: 3
2 1 8 0 1 0 2
Видео:В равнобедренную трапецию Р=40, S=80 можно вписать окружность. Найдите расстояние от точки пересеченСкачать
Вписанная в равнобедренную трапецию окружность
Какими свойствами обладает вписанная в равнобедренную трапецию окружность?
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.
Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
Если MN —
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
По свойству равнобедренной трапеции,
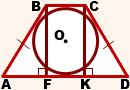
Из прямоугольного треугольника ABF по теореме Пифагора
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
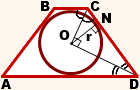
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
📺 Видео
Трапеция. Практическая часть - решение задачи. 8 класс.Скачать
В равнобедренную трапецию, периметр которой равен 180, а площадьравна 1620, можно вписать...Скачать
№700. Докажите, что в любой ромб можно вписать окружность.Скачать
Задача про трапецию, описанную около окружностиСкачать
Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать
В любой ромб можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Кто нибудь знает при каких условиях в трапецию можно вписать окружность Как описать тест УчителюСкачать
8 класс, 38 урок, Вписанная окружностьСкачать
Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать
19 задание огэ математика 2023 ВСЕ ТИПЫ геометрияСкачать
Любой прямоугольник можно вписать в окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Если в четырёхугольник можно вписать окружностьСкачать
Стереометрия 10 класс. Часть 1 | МатематикаСкачать
Окружность, вписанная в четырёхугольник | МатематикаСкачать
Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать
СРЕДНЯЯ ЛИНИЯ. ТРАПЕЦИЯ. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. Контрольная № 2 Геометрия 8 классСкачать
Через любую точку, лежащую вне окружности ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Разбор задания 13 ОГЭ по математикеСкачать
