Логико математический анализ темы треугольники (5 видео)

Логико-математический анализ темы: «Подобие треугольников»

В школьном курсе геометрии тема ‘Подобие треугольников’ рассматриваются в 8 классе.

В учебнике по “Геометрии 7-9 класс” Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина данная тема рассматривается после темы “Площади”.

Возьмем этот учебник за основной и проанализируем его:

1. Структурные особенности ученика.

1.1. Учебник одновременно является задачником, каждый параграф состоит из теоретической и задачной части.

1.2. Материал учебника состоит из 14 глав, каждая из которых разбита на параграфы. Весь теоретический материал учебника разбит на 127 пунктов, нумерация пунктов сквозная.

В каждом параграфе задачный материал следует за теоретическим.

1.3. Задачный материал представляет собой: вопросы и задачи, дополнительные задачи, а также в некоторых параграфах отдельным блоком выделены задачи на применение знаний изученных в параграфе при решении конкретных задач (Применение векторов к решению задач, средняя линия трапеции).

1.4. При изложении материала для выделения главного используется жирный шрифт и обособление цветом. Встречаются исторические справки по теме параграфа. На форзаце учебника помещены признаки равенства и подобия треугольников, формулы площадей, теорема синусов и косинусов, простейшие действия с векторами. К каждой формуле представлен чертеж. Также рисунки представлены при объяснении учебного материала.

2. Методические особенности учебника.

2.1. Теоретический материал изложен дедуктивным методом. Новые предложения выводятся логическим путем из ранее известных предложений.

2.2. Важные моменты учебного материала (правила, теоремы, определения) выделены красной полосой над текстом. Каждое понятие сопровождается рисунком для наглядного представления и лучшего понимания данного понятия.

2.3. В конце каждой главы имеется материал для повторения выделенный отдельным блоком.

2.5. В конце учебника имеются приложения содержащие интересную и полезную информацию. Приведены ответы и указания к упражнениям и предметный указатель.

2.5. Нет разбиения материала на работу в классе и домашнюю работу, эта возможность предоставлена учителю.

3.1. В учебнике четко выделен теоретический и задачный материал, материал для запоминания.

3.2. Каждое понятие сопровождается рисунком или чертежом.

3.3. Содержание учебника соответствует программе для общеобразовательных школ, гимназий, лицеев.

Проанализируем учебник “Геометрия 7-11” Погорелова А.В.

Тема подобие фигур рассматривается после параграфа векторы, что отличает его от предыдущего.

1.Сруктурные особенности учебника.

1.1. Учебник одновременно является и задачником, т.е. все параграфы состоят из теоретической и задачной части.

1.2. Материал учебника разделен на два раздела планиметрия(7,8,9 класс) и стереометрия(10,11 класс) и состоит из 22 параграфов, нумерация параграфов сквозная, каждый из параграфов разделен на пункты, нумерация пунктов также сквозная.

Каждый параграф содержит теоретический материал и примеры или задачи на применение данного материала, после теории отдельными пунктами следуют контрольные вопросы по теме параграфа и задачный материал.

1.3. Задачный материал не разделяется на блоки, задания повышенной трудности помечены знаком «*».

В основном присутствуют текстовые задачи.

1.4 При изложении материала не используются дополнительные цвета, важный материал выделен курсивом или жирным шрифтом На форзаце учебника размещены объёмы и поверхности тел, признаки равенства треугольников, признаки параллельности прямых, соотношения в треугольнике, значения тригонометрических величин, буквы греческого и латинского алфавитов.

2. Методические особенности учебника.

2.1 Теоретический материал рассматривается дедуктивным методом.

2.2. Материал для заучивания формулировки теорем и утверждений выделяются жирным шрифтом, а определяемые понятия курсивом.

Анализ и коррекция причин эмоционально личностной дезадаптации школьника
Как это хорошо известно из детской психологии, любое нормальное развитие ребенка не обходится без определенных кризисов (Л. И. Божович, Д. Б. Эльконин и др.). В период кризисов ребенок переживает состояние повышенного психического напряжения, так как новая социальная ситуация развития предъявляет н .

Понятие «леворукость»
Изучение особенностей левшей осложняется тем, что левши вовсе не являются однородной группой. Существуют различные причины левшества, от которых может зависеть развитие тех или иных качеств у ребенка. Кроме того, встречается «скрытое левшество». Но и это не все. Ребенок может быть леворуким, но не .

Анализ комплексных воспитательно-образовательных программ и парциальных программ по экологическому воспитанию для дошкольных образовательных учреждений
Во второй главе нашего исследования мы проанализировали ряд комплексных воспитательно-образовательных программ и парциальных программ по экологическому воспитанию дошкольников с целью — определить, обращается ли внимание в данных экологических программах на развитие речи детей старших дошкольников. .

Содержание

Элементы рабочей программы учителя по математике
Логико-дидактический анализ темы «Треугольники».
У: А давайте поможем незнайке найти сколько ему надо проплыть по маршруту Кос – Патмос– Астипалея ?
Технологическая карта урока
Логико-математический анализ урока;
Цели, задачи урока;
Методика работы с понятием и с теоремой;
Анализ задачного материала;
Методика работы с одной задачей;
Формы контроля;
Логико-дидактический анализ темы «Подобные треугольники » по учебнику Атанасяна Л.С.
📹 Видео

Видео:Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Элементы рабочей программы учителя по математике

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Логико-дидактический анализ темы «Треугольники».

Треугольник является важнейшей фигурой планиметрии, и потому в первую очередь изучают элементы и свойства этой фигуры. С треугольником связаны многие методы, используемые при решении различных геометрических задач. В школьном курсе геометрии тему «Треугольники» изучают в 7 классе в первом полугодии, далее в 8 классе изучается подобие треугольников, формулы площади треугольников. На протяжении всего курса общеобразовательного обучения Геометрии ученики сталкиваются с треугольниками. Рассмотрим изучение треугольников в 7 классе. А именно главу 2.

Выработать умение: распознавать и изображать треугольники на чертежах и рисунках; сформулировать и доказывать первый, второй и третий признак равенства треугольников, теорему о перпендикуляре к прямой, теоремы о свойствах равнобедренного треугольника; решать задачи, связанные с признаками и свойствами треугольников, несложные задачи на построение с помощью циркуля и линейки.

Иметь представление: что такое теорема и доказательство теоремы, о геометрической фигуре «треугольник» его элементах; о перпендикуляре к прямой, медиане, биссектрисе и высоте треугольника, и их свойствах; о равнобедренном треугольнике.

В изучении этой темы включены:

Основные определения (треугольника, перпендикуляра к прямой, медианы, высоты, биссектрисы, окружности и др.);

Применение теорем в решении задач;

Задачи на построение с помощью циркуля и линейки.

Весь курс по теме «Треугольники» строится в систематическом порядке. Степень сложности упражнений и их решения постепенно усиливается. Есть условные обозначения в каждой теме для запоминания и материал, который важно знать.

Ожидаемые результаты – ученики должны уметь распознавать треугольники; доказывать теоремы на первый, второй и третий признак равенства треугольников, на свойства равнобедренного треугольника; проводить доказательные рассуждения при решении задач; решать задачи на построение с помощью циркуля и линейки.

Обязательные результаты обучения теме:

Таким образом, в ходе работы над темой в школьном курсе алгебры 7 класса учащиеся

определение треугольника, равнобедренного и равностороннего треугольника;

определение перпендикуляра к прямой, медианы, высоты и биссектрисы;

три признака равенства треугольников;

свойства равнобедренного треугольника;

теорему о перпендикуляре к прямой.

определять вид треугольника (остроугольный, прямоугольный, тупоугольный равнобедренный, равносторонний, разносторнние);

применять признаки равенств треугольников в решении задач;

применять свойства равнобедренного треугольника в решении задач;

доказательно рассуждать при решении задач;

делать построения с помощью циркуля и линейки.

Метапредметным результатом изучения курса является формирование универсальных учебных действий (УУД).

В ходе изучения темы учащийся должен извлекать необходимую информацию. Применять полученные знания при решении различного вида задач.

Учащиеся самостоятельно выбирают уровень освоения темы, выбирают задачи. Осуществляют самопроверку, составляют план своих действий при изучении темы и оценивают свою работу, свои действия при изучении темы.

При изучении данной темы учащийся должен научиться высказывать свои мысли, формулировать вопросы и участвовать в дискуссии по теме, работать в группе, давать полные формулировки. Учащийся учиться разбирать и анализировать ошибки в ходе решения. Ученику даётся возможность выступить с сообщением по теме «Треугольники».

Личностные универсальные учебные действия включают: смысло-образование, нравственно-этическое оценивание, самопознание и самоопределение. На уроках по данной теме ученик должен определиться с результатами своей деятельности при решении задач на данную тему, своих мотивов.

Логико-математические связей понятия «Треугольники»

Включения историко-математического материала при изучении темы «Треугольники»

При изучении данной темы может быть рассмотрен следующий перечень вопросов:

История возникновения треугольников;

Треугольники в жизни человека;

Логико-дидактического анализа учебного материала темы «Треугольники»

При проведении логико-дидактического анализа выделены особенности структурного построения и методического изложения материала учебника, определено представление задачного материала. На основании данного анализа сделаны выводы.

Компоненты анализа учебника

Геометрия 7-9 класс (учебник) Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.

Материал в учебнике по данной теме представлен в второй главе в § 1, 2, 3, 4. Каждый параграф делится на пункты. Упражнения и вопросы следуют после параграфов.

Представление задачного материала

Задачный материал разбит на следующие основные блоки в соответствии с теоретическим материалом

Отработка основных понятий, связанных с треугольниками и его элементами;

Первый признак равенства треугольников;

Свойства равнобедренного треугольника;

Второй и третий признак равенства треугольников;

Задачи на построение с помощью циркуля и линейки.

представление текста задачи

В § 1 и 2 есть Практические задание для отработки определений и задачи среднего уровня сложности.

В § 3 и 4 Вопросы и задачи среднего уровня сложности.

В конце главы есть вопросы для повторения и дополнительные задачи, содержащие задания уровнем выше среднего, и задания повышенной сложности, отмеченные значком *

Другие структурные особенности

При изложении материала используются: Определения, теоремы, разобраны доказательства теорем, алгоритмы построения с помощью циркуля и линейки, вопросы для повторения.

Теоретический материал рассматривается в начале каждого параграфа, далее следуют задания и задачи на отработку практических навыков. Стиль изложения доступный. В конце каждой главы присутствуют вопросы на повторение и дополнительные задачи.

использование цвета, особых выделений главного

Материал для запоминания выделен жирным шрифтом.

Имеются рисунки и чертежи для наглядного представления теоретического и задачного материала.

Задачи на повторение расположены только в конце учебника.

Доступно излагается теоретический материал. Много заданий на отработку материала.

Анализ дидактической единицы темы

В теме представлены понятия: теорема, доказательство, треугольник и его элементы, свойства равнобедренного треугольника, окружность. Признаки равенства треугольников. Решение задач при помощи теорем, рассмотренных в данной главе.

Основная цель – выработать умения решать задачи с помощью признаков равенства треугольников, свойств равнобедренного треугольника.

В начале темы приводятся примеры решения задач на нахождение элементов треугольников с помощью теорем. Этот материал систематизируется.

Учащиеся овладевают способом решения задач на построения геометрических фигур с помощью чертежных инструментов.

Анализ задачного материала темы

При проведении анализа задачного материала темы определён вид задач и их дидактическая цель. Задачный материал классифицирован по способу задания, характеру требования, способу решения.

По характеру требования

По дидактической цели

На первый признак равенства треугольников

Задачи представлены математическим текстом

Начертить треугольник и выполнить условия

Отработка первого признака равенства треугольников

На первый признак равенства треугольников

Задачи представлены математическим текстом. №90-99

Доказать, что треугольники равны или найти элементы треугольника

Отработка первого признака равенства треугольников

На свойства равнобедренного треугольника и элемента треугольника

Задачи представлены математическим текстом. №100-104

Начертить треугольник и выполнить условия

Отработка свойств равнобедренного треугольника, первого равенства треугольников, нахождение элементов треугольника

На свойства равнобедренного треугольника и элемента треугольника

Задачи представлены математическим текстом. №105-120

Доказать, что треугольники равны или найти элементы треугольника

На второй и третий признак равенства треугольников

Задачи представлены математическим текстом. №121-142

Доказать, что треугольники равны или найти элементы треугольника

Отработка второго и третьего признака равенства треугольников и нахождение элементов треугольников.

Задачи на построение

Задачи представлены математическим текстом. №143-147

Доказать равенство углов или хорд.

Нахождение углов и хорд.

Задачи на построение

Задачи представлены математическим текстом. №148-155

Отработка умения решать задачи на построение с помощью графических инструментов

В результате выполнения анализа задач была проведена их классификация по уровню сложности и виду:

Задачи на первый признак равенства треугольников

Задачи на свойства равнобедренного треугольника

Задачи на второй и третий признак равенства треугольников

Задачи на построение с помощью циркуля и линейки

Ход урока на тему: « Глава 2. Треугольники. §2 Медианы, биссектрисы и высоты треугольника. п. 18 Свойства равнобедренного треугольника.»

Организационный момент (1 минуты)

Учитель(У): Ребята! Я рада вас видеть сегодня на уроке в хорошем настроении. Ведь самый лучший день

У: Самый лучший отдых?

У: Самая лучшая работа?

У: Самая большая потребность?

У: Самая большая радость?

У: Самая главная задача для нас?

У: А теперь улыбнитесь друг другу и пожелайте хорошего настроения на уроке.

Д: *Поворачиваются к соседу по парте и желают хорошего урока*

У: Я тоже вам желаю сегодня хорошей работы. У кого-нибудь есть вопросы по Домашнему заданию?

Актуализация знаний (3 минуты)

У: Давайте вспомним, что такое треугольник? Что называется, вершиной и стороной треугольника.

Д: Это геометрическая фигура, которая состоит из 3 точек, не лежащих на одной прямой, и трех отрезков попарно соединяющие точки. Где отрезки называются сторонами треугольника, а точка соединяющая две стороны называется вершиной треугольника.

У: Что такое периметр?

Д: Сумма длин всех сторон.

У: А давайте поможем незнайке найти сколько ему надо проплыть по маршруту Кос – Патмос– Астипалея ?

У: Ребят, а какие треугольники мы с Вами уже знаем?

Д: Остроугольные, тупоугольные, прямоугольные. (они же в 4 классе уже оговаривают это. Прямоугольные точно знают)

У: А как вы думаете все ли мы знаем о треугольниках?

Д: Нет. Мне кажется, мы много еще не знаем, возможно, есть какие-нибудь другие виды треугольников.

Изучение нового материала (15 минут)

У: Сегодня мы на уроке узнаем новые виды треугольников: Разносторонние, равнобедренные и равносторонние. Поподробнее рассмотрим равнобедренный треугольник и дадим определение равносторонним и разносторонним треугольников.

Давайте откроем свои тетрадочки и запишем тему урока «Свойства равнобедренного треугольника»

Посмотрите на доску. Как вы думаете, какой треугольник равносторонний? Равнобедренный? Разносторонний?

Д: Первый- равносторонний, второй- разносторонний, третий- равнобедренный.

У: А где мы могли видеть эти треугольники в жизни?

Д: Равнобедренный: крыша дома, грани пирамид, украшения, орнаменты на тканях и т.д. Равносторонние: булочки в столовой (треугольные), пакеты с молоком (которые выдавали в 4 классе) и т.д.

У: Правильно! А Почему вы выбрали именно крушу дома, булочки? По каким признакам вы отбирали, ведь нас окружают столько треугольников?

Д: У равностороннего треугольника все стороны равны. А у равнобедренного треугольника 2 стороны равны. У разностороннего треугольника все стороны разной длинны.

У: Хорошо! Вот вы сами определили, какой треугольник будем называть равнобедренным, разносторонний, а какой равносторонний. Сформулируйте определение равнобедренного треугольника и равностороннего.

Д: Треугольник называется равнобедренным, если две его стороны равны. И равносторонний если все стороны равны.

У: Правильно, но есть еще один признак по которому можно определить какого вида этот треугольник. Давайте посмотрим, что нам предлагает автор нашего учебника. откройте страницу 35.

Д: *открывают учебник. Один из учеников читает определение в слух*

У: Какой признак у треугольников мы не заметили?

У: Давайте в своих конспектах запишем определение и рядом сделаем рисуночки. У равнобедренного треугольника подпишем какие стороны как называются. (все делается параллельно и на доске — учителем, и еще раз обговаривается все детали определений (равенство сторон, углов)

У: О разносторонним треугольнике мы больше ничего не можем сказать. Ни про равенство его углов, ни сторон. Давайте запишем определение. *Диктует определение*.

Таким образом, разносторонние треугольники можно нарисовать по-разному, но чтобы ни стороны, ни углы не были равны.

Равносторонний треугольник начертить можно тоже по-разному, можно его переворачивать, крутить под определенным углом, увеличивать/уменьшать его сторону. Но он всегда будет остроугольный т.к его углы все равны 60°.

Что же можно сказать о равнобедренном треугольнике? Может ли он быть прямоугольный? А остроугольный? А тупоугольный?

У: Вася, изобрази на доске равнобедренный тупоугольный треугольник. Лена, а ты равнобедренный прямоугольный. Вова, а ты попробуй начертить равнобедренный остроугольный.

У: Ребят покажите на рисунке какие углы и стороны равны.

У: А ни у кого не возникает вопрос «Почему мы говорим, что у равнобедренных треугольников точно углы при основаниях равны?»

У: Это одно из свойств равнобедренных треугольников. А давайте это докажем.

Я на доске вы в своих тетрадочках.

В равнобедренном треугольнике углы при основании равны:

— Что надо доказать?

— Как нам можно это доказать? Какие треугольники равны? Почему они равны? Что из этого следует?

Доказать, что А=С.

Построим ВД – биссектрису треугольника АВС.

ВАД= ВСД -по I признаку равенства треугольников т.к.

ВА=ВС (по условию),

1=2 (ВД — биссектриса)).

Из равенства треугольников ВАД и ВСД следует, что А=С. Теорема доказана.

Есть еще одно свойство у равнобедренных треугольников, но об этом мы поговорим на следующем уроке.

У: Давайте сделаем физминутку:

Физминутка для улучшения мозгового кровообращения.

Исходное положение – сидя на стуле. Отвести голову назад и плавно наклонить назад, на счет 1-2, 3-4 – голову наклонить вперед. Повторить 3 раза.

Исходное положение – сидя, руки на поясе. 1- поворот головы налево, 2 – И.п., 3 поворот головы направо, 4 – И.п. Повторить 3 раза.

Исходное положение – стоя или сидя, руки на поясе. 1 – махом левую руку занести через правое плечо, голову повернуть налево, 2- И.п., 3 – то же правой рукой, 4 – И.п. Повторить 3 раза.

Физминутка для снятия напряжения с глаз.

1) Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5.

2) Крепко зажмурить глаза (считать до 3, открыть их и посмотреть вдаль (считать до 5)).

3) Вытянуть правую руку вперед. Следить глазами, не поворачивая головы, за медленными движениями указательного пальца вытянутой руки влево и вправо, вверх и вниз.

4) В среднем темпе проделать 3-4 круговых движения глазами в правую сторону, столько же в левую сторону. Расслабив глазные мышцы, посмотреть вдаль.

Первичное закрепление (10 минут)

У: Отдохнули, поразмялись. А теперь порешаем задачки. Список номеров, которые надо решить в классе – на доске (номер 108, 112, 116 (устно))

Первичный контроль (7 минут)

Раздается каждому ученику по карточке. Всего 4 варианта. Через 7 минут карточки собираются.

2. В равнобедренном треугольнике основание равно 7см, а периметр равен 17см. Вычислите боковую сторону треугольника.

Найдите KBA.

3. В равнобедренном треугольнике боковая сторона равна 6см, а периметр 22см. Вычислите основание треугольника.

4. В равностороннем треугольнике периметр равен 21см. Вычислите сторону треугольника.

Найдите KBA.

Подведение итогов урока (5 минут)

У: Вы сегодня огромные молодцы. Давайте обсудим, что нового сегодня мы узнали.

Д: По очереди – Я научился…Было трудно…Сегодня я узнал…У меня получилось…Теперь я могу…

Информация о домашнем задании (1 минута)

У: Хорошего Вам дня! Домашнее задание на доске (п.18 учить определение и доказательство теоремы. №107,117. При помощи линейки начертить равнобедренный треугольник, вырезать и проверить равенство углов при основании. И наоборот. При помощи циркуля начертить треугольник и проверить равенство сторон)

В тетрадях учеников:

П 18. Свойства равнобедренного треугольника.

Треугольник, все стороны и углы которого равны, называется равносторонним.

Треугольник называется равнобедренным, если две его стороны равны.

Равные стороны называются боковыми, а третья сторона – основанием равнобедренного треугольника.

Разносторонним называется треугольник, у которого все стороны имеют разную длину.

Теорема: В равнобедренном треугольнике углы при основании равны.

Построим ВД – биссектрису треугольника АВС.

ВАД= ВСД -по I признаку равенства треугольников т.к.

ВА=ВС (по условию),

1=2 (ВД — биссектриса)).

Из равенства треугольников ВАД и ВСД следует, что А=С. Теорема доказана.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Технологическая карта урока

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

2. Актуализация знаний (3 мин.)

Актуализация опорных знаний, понадобившихся на уроке.

Напомнить детям основные определения. Подвести учеников к теме урока.

Активно отвечают на вопросы учителя. Повторяют изученный ранее материал.

Коммуникативные: умение выражать свои мысли,

Познавательные: умение строить высказывания, формулирование проблемы.

3. Изучение нового материала (15 мин.)

Обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы.

Сформулировать вместе с детьми основные определения.

Направлять учеников в решении задач.

Вникать в новый материал,

Умение ориентироваться в учебнике;

понимание каждым ребенком правила и теоремы;

умение логически рассуждать и сделать правильный вывод из доказанного;

проявляют положи тельные эмоции при встрече с новым;

-участвуют в коллективном поиске решения учебной задачи;

-выдвигают свои предложения;

-инициативны в дискуссии.

Коммуникативные: постановка вопросов, инициативное сотрудничество.

Познавательные: самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство.

Регулятивные: планирование, прогнозирование.

4. Рефлексия ( 3 мин.)

Применение физминутки помогает детям снять напряжение, побуждает к дальнейшей деятельности, усиливает веру в свои возможности, переключает внимание.

После снятия утомления, учащиеся продолжают деятельность переходят к закреплению изученного материала.

5.Первичное закрепление знаний

Установление правильности и осознанности изучения темы.

Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу.

Организует работу учащихся. Помогает в правильности решения задач. Направляет на правильность решения.

Ребята делают предположения, обосновывают свои ответы, записывают решение в тетрадях. Сверяют с доской.

Регулятивные: контроль, оценка, коррекция.

Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач.

Коммуникативные: контроль, коррекция.

6.Первичный контроля ( 7 мин.)

Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков.

Самостоятельная работа в 4 вариантах. Состоит из 2 номеров. Первая на нахождение сторон. Вторая на нахождения углов при помощи теоремы.

Самостоятельное решение в тетради.

Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;

7. Подведение итогов урока.(5 мин.)

Дать качественную оценку работы класса и отдельных обучаемых

-Что изучили сегодня на уроке?

Какие были трудности на пути изучения нового материала. Что, наоборот, давалось без затруднений. Оценить отдельных учащихся.

Оценивают свою работу на уроке. Подводят итоги по усвоению материала.

Регулятивные: оценка-осознание уровня и качества усвоения; контроль

8. Информация о домашнем задании (1 мин)

Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.

Формулирует домашнее задание, записывает номера задач на доске, отвечает на вопросы учащихся.

Записывают домашнее задание в дневник, читают задачи, задают вопросы.

Видео:Треугольник ПаскаляСкачать

Логико-математический анализ урока;

Цель: Формировать знание понятия равнобедренного треугольника, его элементов, свойств углов при основании равнобедренного треугольника, навыки применения полученных знаний при решении задач.

Выделяются основные теоретические части: Виды треугольников (?)Треугольники бывают – остроугольные, прямоугольные, тупоугольные.

Выделение основных задач: Задачи на прямое применения теорем. Задачи, решающие при помощи полученных ранее и новых знаний. Задачи на нахождении длины стороны. Задачи на нахождение углов.

Установление взаимосвязи материала темы и ранее изученного материала: На данном уроке нам надо было актуализировать знания, полученные ранее, а именно вспомнить в целом, что такое треугольник (вершина, стороны, углы — внешние/внутренние) На какие виды делятся треугольники (остроугольные, прямоугольные, тупоугольные). Как находится периметр (для решения задач) Первый признак равенства треугольников. Понятия биссектрисы, высоты и медианы.

В процессе обучения целесообразно использовать следующие формы контроля:

Самостоятельные работы (воспроизведения, прямого назначения и творческие применения)

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Цели, задачи урока;

Цель урока: изучить и доказать свойства равнобедренного треугольника.

повторить основные понятия по теме «Треугольник»,

изучить какие треугольники называются равнобедренные и равносторонние;

доказать свойства равнобедренного треугольника;

формировать умение применять эти свойства,

развивать логическое и пространственное мышление, творческую и мыслительную деятельность учащихся, способность к «видению» проблемы;

формировать способности к оценке собственной деятельности,

формировать осознанное и ответственное отношение к своей деятельности;

формировать информационную и коммуникативную компетенции.

Тип урока : урок изучения нового материала.

Оборудование и материалы урока : компьютер, интерактивная доска, проектор, презентация; раздаточный материал: текст самостоятельной работы.

Организационный момент (1 мин.)

Актуализация знаний (3 мин.)

Изучение нового материала (15 мин.)

Физ.минутка (3 мин.)

Первичное закрепление знаний (10 мин.)

Первичный контроля (7 мин.)

Подведение итогов урока (5 мин.)

Информация о домашнем задании (1 мин)

Познавательные: Умение строить высказывания, умение структурировать знания, выбор наиболее эффективных способов решения задач. давать определения понятиям.

Коммуникативные: умения выражать свои мысли,

Видео:Решение задач на тему "Подобные треугольники". 8 классСкачать

Методика работы с понятием и с теоремой;

Определение: Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием

С данным определение я согласна. Лишнего нет. В будущем я бы проговаривала с детьми о равенстве углов. (Треугольник называется равнобедренным, если 2 стороны и 2 угла прилежащие к основанию называется равнобедренным) Но так как мы изучаем равнобедренные треугольники впервые, то мы обговариваем это в теореме.

Теорема: В равнобедренном треугольнике углы при основании равны.

Мотивация изучения теоремы и раскрытие ее содержания.

После прочтения определения данный автором, детям было предложено на доске изобразить разные виды равнобедренных треугольников и отметить равные элементы. На что потом был задан вопрос «Почему мы утверждаем равенство углов?» Детки начали предполагать. В итоге пришли к выводу, что это не так очевидно и надо это доказать.

Доказательства теоремы (все в конспекте)

Закрепление теоремы. Еще раз проговорить теорему и начать решать задачи (т.к. это первичные урок то вы решаем в основном прямые задачи и явные.).

Говорим деткам, что существует обратная теорема, но для ее доказательства нам надо еще кое-то узнать.

Видео:Задача, которую боятсяСкачать

Анализ задачного материала;

По характеру требования

По дидактической цели

На определение равнобедренного треугольника

Задачи представлены математическим текстом.

Найти стороны треугольника

Отработка определения равнобедренного треугольника

На свойства равнобедренного треугольника, свойства вертикальных углов.

Задачи представлены математическим текстом. с представленным рисунком

Доказать, что углы равны

Провести доказательные рассуждения

Отработка свойств равнобедренного треугольника, повторения свойства углов

На свойства равнобедренного треугольника

Задачи представлены математическим текстом.

Найти стороны треугольника

Отработка определения равнобедренного треугольника.

На свойства равнобедренного треугольника

Задачи представлены математическим текстом. с представленным рисунком

Отработка свойств равнобедренного треугольника.

На свойства равнобедренного треугольника и элементы равнобедренного треугольника

Задачи представлены математическим текстом.

Найти элементы треугольника

Провести доказательные рассуждения

Отработка свойств р/б треугольника

Задачи в случае быстрого темпа (на запас)

На свойства равнобедренного треугольника, элемента треугольника и первый признак равенства треугольников

Задачи представлены математическим текстом.

Доказать, что треугольник(и) равны или найти элементы треугольника

Провести доказательные рассуждения

Отработка свойств равнобедренного треугольника, первого равенства треугольников.

На свойства равнобедренного треугольника и элементы р/б треугольника

Задачи представлены математическим текстом.

Найти элементы треугольника

Отработка свойств р/б треугольника

В самостоятельной работе

На свойства равнобедренного треугольника

Задачи представлены математическим текстом.

Найти стороны треугольника

Отработка определения равнобедренного треугольника.

На свойства равнобедренного треугольника

Задачи представлены математическим текстом. с представленным рисунком.

Найти углы треугольника

Отработка свойств равнобедренного треугольника.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Методика работы с одной задачей;

При решении геометрических задач обычно используются три основных метода: геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем. Алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений. Комбинированный – когда на одних этапах решение ведется геометрическим методом, а на других — алгебраическим.

Решим Задачу 117 на стр. 37.

Эта задача позволит отработать свойства р/б треугольников.

На рисунке дано 2 равнобедренных треугольника с общей вершиной. Надо доказать, что 2 угла равны. Доказательство данной задачи является прямым (можно построить цепочку рассуждений от условия к заключения..без дополнительных построений.). Решается она только при помощи знания о равнобедренных треугольниках и его свойствах +вертикальные углы.

Подведение детей на решение данной задачи.

Рассмотреть каждый равнобедренный треугольник по отдельности. Детки быстро сообразят о равенстве углов.

Рассмотрим вертикальные углы. По свойству вертикальных углов они равны.

Из вышесказанного можно делать вывод о равенстве нужных углов. Обговорив с детьми о равенстве всех рассмотренных углов.

Какие могут возникнуть проблемы /вопросы:

Не сообразили/вспомнили о вертикальных углах.

Начали искать решение данной задачи в первом признаке треугольников.

Доказать: CAB =С ED

Рассмотрим  DCE – равнобедренный.

По теореме  DCE= С ED.

Рассмотрим  ABC – равнобедренный.

По теореме  BCA=CAB.

 BCA = DCE – как вертикальные углы.

Т.к. CAB =  BCA =  DCE =  С ED из этого следует

При решении задач ученик получает возможность:

овладеть символическим языком геометрии;

развить изобразительные умения;

развить логическое мышление и речь – умения логически обосновывать суждения;

проводить несложные систематизации;

использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства в решении задач

Формируются такие УУД:

креативность мышления, инициатива, находчивость, активность при решении геометрических задач;

способность к восприятию математических объектов, задач, решений, рассуждений;

умение строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;

умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;

умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;

умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы;

умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;

умение контролировать процесс и результат учебной математической деятельности;

умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения.

Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

Формы контроля;

Вид контроля: входной контроль

Формы организации контроля: т.к. у нас это первичный контроль данного пункта, то я бы устроила самостоятельную работу с самоконтролем (а на 2ом уроке самостоятельную работу в конце урока по всему пункту или через урок в начале (после выполненного ДЗ и заданных вопросов по нему)).

Формы контроля: Самооценка учащихся своих работ. На дом даю что-то на подобие лабораторной контрольной.

Сама самостоятельная работа: Состоит из 4 вариантов. По сложности все варианты одинаковые (можно для умненьких сделать посложнее, но я этого делать не стала т.к все же первичный контроль и все же не на оценку.). Как уже где-то выше писалось в первом задании задачи на нахождение сторон (через периметр), во втором номере надо найти углы с помощью изученной теоремы, так же в некоторых задачах понадобится знания свойств о смежных и вертикальных углах.

Найдите KBA.

3. В равнобедренном треугольнике боковая сторона равна 6см, а периметр 22см. Вычислите основание треугольника.

4. В равностороннем треугольнике периметр равен 21см. Вычислите сторону треугольника.

Найдите KBA.

Система оценивания: Самоконтроль. Посчитать сколько человек решили все задачи, сколько по одной. Выяснить какие трудности были в решении данных задач, и учесть их в планировании следующего урока.

Помимо этого, есть контроль домашнего задания. Проверить у всех наличие ДЗ у всех, у кого нет совсем ничего оценить его в оценку 1. Ответить на вопросы учеников. Кое-какие сделать на доске. После главы 2 собрать тетрадки и выставить среднюю оценку за главу по ДЗ.

Видео:Вся геометрия 7–9 класс с нуля | ОГЭ МАТЕМАТИКА 2023Скачать

Логико-дидактический анализ темы «Подобные треугольники » по учебнику Атанасяна Л.С.

Тема подобные треугольники в учебнике Атанасяна Л.С. вводиться в 8 классе и включает в себя четыре параграфа, каждый из которых делиться на пункты.

§1. Определение подобных треугольников.

§2. Признаки подобия треугольников.

§3. Применение подобия к доказательству теорем и решению задач.

§4. соотношения между сторонами и углами прямоугольного треугольника.

В первом параграфе вводятся такие новые понятия как «пропорциональные отрезки», «сходственные стороны», «подобные треугольники», «коэффициент подобия».

Понятие пропорциональных отрезков вводиться описательно с использованием ранее изученного факта (об отношении двух отрезков), и рассматривается конкретный пример на применение нового определения. Далее оговаривается, что понятие пропорциональности может вводиться и для большого числа отрезков.

Прежде чем ввести определение подобных треугольников предлагается разобраться с подобием в реальной и повседневной жизни, и с подобием фигур в геометрии вообще. После этого используя рисунок двух треугольников и равенство углов описательно вводиться определение сходственных сторон. После словесной формулировки предлагается другая запись с использованием буквенной символики, таким образом, подобие треугольников даётся не на основе преобразования подобия, а через равенство углов и пропорциональности сходственных сторон. Пусть треугольники АВС и А₁В₁С₁ подобны тогда (1); (2) из последнего отношения вытекает понятие коэффициента подобия.

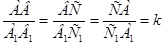
Рассмотрев все основные понятия анализируемого параграфа, переходят к изучению следующей теоремы: «Отношение площадей подобных треугольников равно квадрату коэффициента подобия», доказательство основано на применение теоремы об отношении площадей треугольника, имеющих по равному углу и определение подобных треугольников.

Во втором параграфе рассматриваются только признаки подобия треугольников с доказательством и отсутствуют новые понятия.

Оказывается, что подобие треугольников можно установить, проверив только некоторые из равенств определения подобных треугольников (1) или (2). Для доказательства этого факта рассматриваются три признака подобия треугольников. Первый признак доказывается, опираясь на теорему о сумме углов треугольника и на ранее изученную теорему об отношении площадей треугольников имеющих по одному равному углу. Второй и третий признак доказывается по общей схеме:

1. Рассматривается треугольник АВС₂;

2. Доказывается, что треугольники АВС₂ и А₁В₁С₁ подобны (по первому признаку);

3. Доказывается равенство треугольников АВС и АВС₂.

В изложенном материале третьего параграфа рассматриваются новые понятия: «средняя линия треугольника», «среднее пропорциональное», «метод подобия», каждое из определений вводиться описательно.

Именно в этом параграфе доказывается теорема о средней линии треугольника и на основании этой теоремы решается очень важная задача геометрии: «Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины».

Для доказательства следующих утверждений

1 0 Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делит гипотенуза этой высоты;

2 0 Катет прямоугольного треугольника, есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключённым между катетом и высотой, проведенной из вершины прямого угла; решается задача: «Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных треугольника, каждый из которых подобен данному треугольнику». Решение опирается на рассмотрение различных треугольников и доказательства их подобия.

Для формирования практической значимости подобия треугольников рассматривается метод подобия, после описания, которого предлагаются задачи с решениями.

Уже в последнем пункте вводиться понятие подобия произвольных фигур и коэффициент подобия фигур. Эти понятия вводятся через сопоставление двух точек M, N одной фигуры F, точкам M₁, N₁ другой фигуры F₁ и , где k-одно и тоже положительное число для всех точек. Далее делается вывод, что каждая точка фигуры F₁ оказывается сопоставленной какой-то точке фигуры F. Здесь же предлагается способ построения подобных фигур.

В последнем параграфе анализируемой темы учащиеся знакомятся с элементами тригонометрии, необходимые для решения прямоугольных треугольников. Здесь вводятся новые понятия синуса, косинуса, тангенса. Их определения даются через отношения сторон прямоугольного треугольника друг к другу. Причём тангенс определяется как отношение синуса к косинусу. При рассмотрении данных понятий вводятся их обозначение. Далее формулируется и доказывается утверждение о том, что из равенства острых углов следует равенство значений тригонометрических функций соответствующих данным углам. Сначала доказывается подобие треугольников, из которых следует пропорциональность сходственных сторон треугольников, пользуясь полученными равенствами, получаем доказываемый материал. Здесь же доказывается sin 2 A+cos 2 A=1 называемое основным тригонометрическим тождеством. При доказательстве опираются на новые понятия синуса, косинуса и на теорему Пифагора. Значения синуса, косинуса и тангенса для углов 30 0 , 45 0 , 60 0 находятся через основное тригонометрическое тождество, Через теорему о катете лежащем против угла в 30 0 , через теорему Пифагора. Полученные результаты отображены в таблице. Материал, связанный с подобием, позволяет содержательно реализовать межпредметные связи с алгеброй (пропорциональность, уравнения, квадратичные корни) и с физикой (например, геометрическая оптика). В систему упражнений включено более 50 задач. Большая часть направлена на прямое или опосредованное применение теории. Много задач познавательного характера, способствующие получению новых фактов, которые используются при решении других задач (№534, 537, 569,…), задачи с практическим содержанием (№546, 579, 580, 581, 583,…).

Изучая тему «Подобные треугольники», можно подробно остановиться на примерах из реального мира, необходимо рассказать об истории возникновения и развития подобия, подробно рассказать легенду о Фалесе, который измерил высоту пирамиды без всяких приборов по отбрасываемой ею тени. Познакомить учащихся с золотым треугольником, золотым прямоугольником, золотым сечением, которое является одним из удивительно красивых объектов, интерес к которым проявляли учёные, художники на протяжении многих веков.