Наиболее простым и наглядным методом решения задачи линейного программирования (ЗЛП) является графический метод. Он основан на геометрической интерпретации задачи линейного программирования и применяется при решении ЗЛП с двумя неизвестными:
Будем рассматривать решение этой задачи на плоскости. Каждое неравенство системы функциональных ограничений геометрически определяет полуплоскость с граничной прямой апх, + + aj2х2 = bn i = 1, т. Условия неотрицательности определяют полуплоскости с граничными прямыми х <= 0, х2 = 0 соответственно. Если система совместна, то полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек; координаты каждой из этих точек являются решением данной системы. Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, ограниченным и неограниченным многоугольником.
Геометрически ЗЛП представляет собой отыскание такой угловой точки многоугольника решений, координаты которой доставляют максимальное (минимальное) значение линейной целевой функции, причем допустимыми решениями являются все точки многоугольника решений.
Линейное уравнение описывает множество точек, лежащих на одной прямой. Линейное неравенство описывает некоторую область на плоскости.
Определим, какую часть плоскости описывает неравенство 2х <+ Зх2 0, j = 1, п). Координаты любой точки, принадлежащей области определения, являются допустимым решением задачи.
Для нахождения экстремального значения целевой функции при графическом решении ЗЛП используют вектор-градиент, координаты которого являются частными производными целевой функции:
Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая c[xl + с2х2 = f(x0), перпендикулярная вектору-градиенту, является линией уровня целевой функции (рис. 2.2.2). В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине а. Меняя значение а, получим семейство параллельных прямых, каждая из которых является линией уровня целевой функции.
Рис. 2.2.2. Вектор-градиент и линии уровня
Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в д р у г у ю сторону — только убывает.
Графический метод решения ЗЛП состоит из четырех этапов:
- 1. Строится область допустимых решений (ОДР) ЗЛП.
- 2. Строится вектор-градиент целевой функции (ЦФ) с началом в точке х0 (0; 0): V = (с,, с2).
- 3. Линия уровня CjXj + с2х2 = а (а — постоянная величина) — прямая, перпендикулярная вектору-градиенту V, — передвигается в направлении вектора-градиента в случае максимизации целевой функции f(xv х2) до тех пор, пока не покинет пределов ОДР. При минимизации /(*,, х2) линия уровня перемещается в направлении, противоположном вектору-градиенту. Крайняя точка (или точки) ОДР при этом движении и является точкой максимума (минимума) f(xpjc2).
Если прямая, соответствующая линии уровня, при своем движении не покидает ОДР, то минимума (максимума) функции f(xр х2) не существует.
Если линия уровня целевой функции параллельна функциональному ограничению задачи, на котором достигается оптимальное значение ЦФ, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и, соответственно, любая из этих точек является оптимальным решением ЗЛП.
4. Определяются координаты точки максимума (минимума). Для этого достаточно решить систему уравнений прямых, дающих в пересечении точку максимума (минимума). Значение f(x<, х2), найденное в полученной точке, является максимальным (минимальным) значением целевой функции.
Возможные ситуации графического решения ЗЛП представлены в табл. 2.2.1.
Видео:Графический метод решения задач линейного программирования | Высшая математика TutorOnlineСкачать
Лекции по исследованию операций, учебное пособие (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 |
,
То есть решение Х* также является оптимальным.
Теорема 1 указывает принцип решения задач ЛП: вместо исследования бесконечного множества допустимых решений необходимо исследовать конечное число угловых точек.
1.3. Графический метод решения задачи ЛП с двумя переменными
Дана задача ЛП с двумя переменными
Графический метод решения основан на возможности графического изображения ОДР задачи и нахождения в ней оптимального решения.
1. Строят ОДР задачи как пересечение областей решений каждого из заданных ограничений. ОДР может быть выпуклый многоугольник; выпуклая многоугольная неограниченная область; пустая область; луч; отрезок; единственная точка. Если ОДР является пустым множеством, задача не имеет решения виду несовместности системы ограничений.
2. Если ОДР непусто, определяют направление возрастания целевой функции Z(X).
При произвольном фиксированном значении 
уравнение 
определяет на плоскости 
прямую, являющуюся линией уровня целевой функции − прямой, на которой целевая функция задачи принимает постоянное значение. Общий вид уравнения линии уровня: с1×1+с2×2=l, l=const. Все линии уровня параллельны между собой. Их нормаль 
. Направление 
является направлением возрастания Z(X).
Таким образом, на 2-ом шаге строят нормаль линий уровня и одну из линий уровня (имеющую общие точки с ОДР).
3. Линию уровня перемещают параллельно в направлении нормали в задаче на максимум, в противоположном направлении в задаче на минимум. В какой-то момент она займет предельное положение: 1) будет иметь хотя бы одну общую точку с ОДР, 2) ОДР будет находиться в одной полуплоскости по отношению к линии уровня. Такая линия уровня называется опорной прямой. ОДР любой задачи ЛП имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.
4. Если при перемещении линии уровня по ОДР в соответствующем направлении линия уровня уходит в бесконечность, то задача не имеет оптимального решения ввиду неограниченности целевой функции. Пишут Z(X)→
.
5. Если задача имеет оптимальное решение, для его нахождения необходимо решить совместно уравнения прямых, ограничивающих ОДР и имеющих общие точки с опорной прямой.
6. Вычисляют значение целевой функции на оптимальном решении.
В зависимости от вида ОДР и целевой функции Z(X) задача ЛП может иметь единственное решение, бесконечное множество решений, не иметь оптимального решения (см. рис. 1, 2 ,3).
 | ||||||||
 | ||||||||
На рис.1 линия уровня дважды становится опорной по отношению к многоугольнику решений. Минимальное значение Z(X) достигается в т. А, максимальное – в т. С. На рис.2 опорная прямая совпадает с одной из сторон многоугольника решений. Оптимальным решением является любая выпуклая линейная комбинация точек отрезка АЕ. На рис.3 ОДР не ограничена в сторону увеличения значений Z(X). Пример 1. Решим графически задачу ЛП:
Построим многоугольник решений (рис.4). Для этого в системе координат X10X2 на плоскости изобразим граничные прямые: 3х1 + 2х2 = 13 (L2); Взяв какую-либо точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, на рис.4 показаны стрелками. Областью решений является многоугольник OABCD. Строим линию уровня Z = 3х1 + 4х2 = 0 и вектор-градиент Точка С лежит на пересечении прямых L1 и L3. Для определения ее координат решим систему уравнений:
Оптимальный план задачи х1=2,4; х2=1,4. Подставляя значения х1 и х2 в линейную функцию, получим:
1.4. Решение задач линейного программирования симплекс-методом Приведение задач ЛП к канонической форме Если математическая модель задачи ЛП имеет вид:
то говорят, что задача представлена в канонической форме на минимум (максимум). Более компактная запись: (1) и (2) – координатные записи канонической задачи ЛП. Векторная запись канонической задачи:
где Матричная запись канонической задачи: где Любую задачу ЛП можно свести к канонической по следующим правилам. 1. Переход от задачи на max к задаче на min (и обратно) осуществляется изменением знака целевой функции
Исходная и полученная задачи имеют одно и то же оптимальное решение Х*, а значения целевых функций 2. Если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства
В целевую функцию дополнительные переменные вводятся с нулевыми коэффициентами, в этом случае они не влияют на значение Z(X)
3. Если некоторая переменная xk не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными: Пример 1. Приведем к канонической форме (на минимум) задачу ЛП:
1. Перейдем к задаче на минимум
2. Введем в каждое ограничение системы ограничений выравнивающие переменные x4, x5, x6. Система запишется в виде равенств.
3. В канонической форме записи задач ЛП все переменные, входящие в систему ограничений, должны быть отрицательными. Допустим, что Подставляя данное выражение в систему ограничений и целевую функцию и записывая переменные в порядке возрастания индекса, получим задачу ЛП, представленную в канонической форме:
Принцип работы симплекс-метода Решение задач ЛП на основе симплекс-метода состоит в целенаправленном переборе угловых точек ОДР в направлении улучшения значения целевой функции. Сначала находится какое-либо допустимое решение, соответствующее одной из угловых точек ОДР. Проверяются смежные с ней угловые точки, то есть расположенные на той же границе ОДР, что и текущая угловая точка (для двухмерной ОДР – на той же стороне многоугольника, для трехмерной – на том же ребре многогранника и т. д.). Можно доказать, что переход из одной угловой точки ОДР в другую (смежную) соответствует замене одной переменной в базисе. Такая замена означает, что одна из небазисных переменных (имевшая нулевое значение) включается в базис, т. е. увеличивается, а одна из базисных переменных уменьшается до нуля, т. е. исключается из базиса. Выбор таких переменных выполняется по определенным правилам, обеспечивающим максимально быстрое улучшение целевой функции. Если ни в одной из смежных угловых точек значение целевой функции не улучшается, то решение задачи завершается; текущая угловая точка ОДР соответствует оптимальному решению задачи. Если имеются смежные угловые точки ОДР, для которых значение целевой функции улучшается, то выполняется переход в ту из них, для которой достигается наиболее быстрое улучшение значения целевой функции. Для новой угловой точки ОДР процесс повторяется. Перебор угловых точек происходит до тех пор, пока не будет найдено оптимальное решение, т. е. пока не будет достигнута угловая точка ОДР, для которой ни в одной из смежных точек значение целевой функции не улучшается. Метод называется симплексным, т. к. области допустимых решений задач, которые рассматривались на начальном этапе развития метода, имели простейший (simple) вид (рис.1):
1.Задача приводится к канонической форме. 2.Строится исходная симплекс-таблица и определяется начальное допустимое решение (начальная угловая точка). 3.Выполняются преобразования симплекс-таблиц, соответствующие перебору угловых точек ОДР, до получения оптимального решения. Рассмотрим реализацию данного алгоритма при решении задачи линейного программирования:
где 1. Перепишем задачу в каноническом виде, добавив дополнительные неизвестные
где 2. Запишем первую симплекс-таблицу: Если в последней строке (среди чисел —c1,…., —c2) нет отрицательных коэффициентов, то базисное решение (когда свободные неизвестные х1 =…= хn =0) будет оптимальным. Действительно, если увеличить от 0 хотя бы одно из свободных неизвестных, то функция будет убывать. Пусть, например, —c1 0, то при равенстве 0 всех остальных свободных неизвестных х1 можно увеличивать не более чем до числа b1/a11. Если a11 3. Ограничимся случаями, когда в первом столбце среди чисел a11,…, ak1 есть положительные коэффициенты: Для новой симплекс-таблицы, если в последней строке нет отрицательных коэффициентов, соответствующее базисное решение будет оптимальным (функция Пример 2. Для выполнения работ по изготовлению изделий 1-го и 2-го типа имеется 10 единиц 1-го сырья и 8 единиц 2-го сырья. На каждое изделие 1-го типа расходуется по 2 единицы каждого сырья, а для каждого изделия 2-го типа расходуется 4 и 1 единицы сырья каждого типа. Спланировать производство так, чтобы суммарное число изделий было наибольшим. Пусть изделий 1-го и 2-го типа производится x1 и x2 единиц, тогда сырья 1-го типа будет израсходовано Введем вспомогательные неизвестные x3 и x4 (остатки сырья 1-го и 2-го типа) и получим каноническую задачу:
где Видео:Графический метод решения задачи линейного программирования (ЗЛП)Скачать  Целевая функция в задаче ЛП с двумя переменнымиВ задаче с двумя переменными целевая функция имеет вид Предположим, что Z = 3x1 + x2. Выясним, как графически можно представить целевую функцию в координатной плоскости Х10Х2. Для этого придадим Z какое-либо постоянное значение, например, Z= 3. Тогда получаем Это уравнение задает в координатной плоскости Х10Х2 прямую с угловым коэффициентом, равным (-3). Напомним, что угловой коэффициент прямой — это коэффициент, стоящий при аргументе х1, который равен тангенсу угла наклона прямой к оси 0Х1 и, следовательно, задает ее наклон. Нанесем эту прямую на график, представленный на рис. 3.5. Заметим, что для всех точек, принадлежащих данной прямой, значение целевой функции одинаково (постоянно) и равно 3, поскольку все точки прямой удовлетворяют уравнению 3х1 + x2=3. Положим теперь Z = 5. Тогда в Х10Х2 получаем новую прямую (рис, 3.5), уравнение которой
Заметим, что угловой коэффициент новой прямой, также как и первой (Z = 3), равен (-3). Следовательно, прямые Z=3и Z=5 параллельны друг другу. Пусть теперь Z = 6. Рассуждая аналогично, можно построить на графике прямую, задаваемую и этим уравнением. Она также будет параллельна первым двум прямым линиям Z = 3 и Z = 5, поскольку угловой коэффициент и в этом случае остался равным (-3). Причем по мере удаления от начала координат величина Z возрастает, а при перемещении к началу координат — уменьшается. Легко прийти к выводу: разным значениям целевой функции Z соответствует семейство параллельных прямых. Для нахождения наибольших и наименьших значений целевой функции необходимо в первую очередь научиться определять, в каком направлении следует перемещать какую-либо линию Z = const, чтобы значение Z возрастало (убывало). Это можно сделать двумя способами. Первый рассмотрен выше: построив пару прямых для разных значений Z и сопоставив их взаимное расположение, определяют направление возрастания или убывания целевой функции. Однако сделать это удобнее на основе использования некоторых сведений из математического анализа, а именно: • Если задана функция двух переменных Z = f(x1 х2), то линии в Х10Х2 для которых Z = f(x1 х2) = const, называют линиями уровня. Иначе говоря, это те линии, во всех точках которых величина Z постоянна. • В задачах линейного программирования линиями уровня являются прямые Z = const. Во всех точках, принадлежащих какой-либо линии уровня, значение целевой функции одинаково. • Важным свойством линий уровня для линейных целевых функций является то, что при их параллельном смещении в одну сторону величина Z только возрастает, а при перемещении в другую сторону — только убывает. • Определить направление возрастания целевой функции можно с помощью специального вектора, называемого градиентом функции Z = f(x1 х2). Для его обозначения используют символ • Вектор-градиент обладает следующим свойством: в каждой точке он перпендикулярен соответствующей линии уровня и указывает направление ее возрастания. • В задачах линейного программирования с целевой функцией Z = с1х1 + c2x2 координатами вектора
x2
Эти утверждения позволяют строить только одну прямую Z = const и далее определять с помощью вектора с координатами Проведенный анализ позволяет сделать следующие выводы. • Эффективным инструментом для анализа поведения целевой функции являются линии уровня. • Линии уровня в задачах линейного программирования с двумя переменными — это прямые, во всех точках которых величина Z постоянна. • Вектор • При изменении коэффициентов (c1, c2) целевой функции Z = с1х1+ c2x2 линии уровня меняют наклон и направление возрастания. 🎦 ВидеоПрямая и двойственная задачи линейного программирования (ЗЛП)Скачать  Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать  Линейное программирование Часть 1. Постановка задачиСкачать  Решение задачи линейного программирования при помощи надстройки Поиск решенияСкачать  Cимплексный метод решения задачи линейного программирования (ЗЛП)Скачать  СИМПЛЕКС МЕТОД: ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯСкачать  Геометрический метод решения задачи линейного программированияСкачать  Математика без Ху!ни. Функции нескольких переменных. Область определения. Линии уровня.Скачать  Урок 2. Экономический смысл двойственной задачиСкачать  Графический метод решения задачи линейного программирования.Скачать  Лекция 1. Комментарии к дистанционной лекции по линейному программированию.Скачать  Практическая работа "Решение задач линейного программирования графическим методом".Скачать  Линейное программированиеСкачать  Практика 2 Способы переходов между формами задач линейного программированияСкачать  Лекция 4 Анализ чувствительности решения задачи линейного программированияСкачать  Симплексный метод (табличный оформление №1) решения задачи линейного программирования.Скачать  Поверхности и линии уровняСкачать  Решение задачи линейного программирования графическим методомСкачать  |
. Прямую Z = 0 перемещаем параллельно самой себе в направлении вектора 
.
(1)
(2)
(3)
(4)
.
на этом решении отличаются лишь знаком.
→ 
→ 
.
, где 
.
.
, где 
.
.
:
0, то неравенство не накладывает ограничений на рост числа х1 (тогда х1 можно увеличивать сколько угодно). Поэтому, если все коэффициенты a11,…, ak1 неположительны, то х1 может расти неограниченно и, при этом, функция 
будет нарастать также неограниченно. В этом случае оптимального решения нет.
, тогда число х1 можно увеличивать до величины x0=min
. Пусть min достигается в строке 
и пусть i1=1. Перейдем к базису, переводя х1 в базис вместо хn+1. Получим новую симплекс-таблицу, для которой значение функции 
х0>0.
, где числа 
,…, 
, а сырья 2-го типа 
. Требуется найти максимум функции 
при неотрицательных целых значениях аргумента.
.
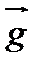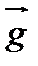=(с1,с2)