Конспект урока
Геометрия, 10 класс
Урок № 8 Перпендикулярность прямой и плоскости
Перечень вопросов, рассматриваемых по теме
- Ввести понятие перпендикулярных прямых в пространстве;
- Доказать лемму о перпендикулярности двух параллельных прямых;
- Решать задачи по теме.
Глоссарий по теме
Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости
Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл. Базовый и профильный уровень. М.: Просвещение, 2015. С.1-10.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 9 класса. Базовый и профильный уровень
Зив Б.Г. Геометрия. Дидактические материалы. 10-11 класс М.: Просвещение, 2015.
Открытые электронные ресурсы:
Перпендикулярность прямой и плоскости. http://school-collection.edu.ru // Единая коллекция цифровых образовательных ресурсов.
Перпендикулярность прямой и плоскости. https://www.yaklass.ru // Я-класс. Образовательный портал Сколково.
Теоретический материал для самостоятельного изучения
Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой..
Через точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с. Так как а ⊥ с, то ∠АМС=90 о .
Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между ними равен 90 о , т.е. b ‖ МА, с ‖ МС, угол между МА и МС равен 90 о
Это означает, что угол между прямыми b и с также равен 90 о , то есть b ⊥ с.
Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Проведем какую-нибудь прямую x в плоскости α, т.е. x ∊ α.Так как а ⊥ α, то а ⊥ x.
По лемме о перпендикулярности двух параллельных прямых к третьей а1 ⊥ x.
Таким образом, прямая а1 перпендикулярна к любой прямой, лежащей в плоскости α, т. е. а1 ⊥ α
Теорема. Ели две прямые перпендикулярны плоскости, то они параллельны.
Через какую-нибудь точку М прямой b проведем прямую b1, параллельную прямой а.
Докажем, что прямая b1 совпадает с прямой b. Тем самым будем доказано, что а ‖ b. Допустим, что прямые b1 и b не совпадают. Тогда в плоскости β, содержащей прямые b и b1, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а ‖ b, т.е. b ∊ β, b1 ∊ β, α 
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.
Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку М проходит единственная прямая с, перпендикулярная плоскости α.
Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b – линия пересечения плоскостей α и γ.
В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.
Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.
Предположим, что существует прямая с1, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с1 перпендикулярны плоскости α. Значит, прямые с и с1 параллельны. Но по построению прямые с и с1пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.
Теоретический материал для углубленного изучения
Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.
Доказательство (см. рис. 1)
Пусть нам дана прямая а и точка М. Докажем, что существует плоскость γ, которая проходит через точку М и которая перпендикулярна прямой а.
Через прямую а проведем плоскости α и β так, что точка М принадлежит плоскости α. Плоскости α и β пересекаются по прямой а. В плоскости α через точку М проведем перпендикуляр MN (или р) к прямой а, 
Примеры и разборы решения заданий тренировочного модуля
Выбор элемента из выпадающего списка
Выпишите ребра, перпендикулярные плоскости (DC
Правильный вариант/варианты (или правильные комбинации вариантов):
Неправильный вариант/варианты (или комбинации):
Подсказка: в кубе все углы по 


- Разбор задания: Куб – это геометрическая фигура у которой все углы прямые, следовательно нужно увидеть ребра которые перпендикулярны к плоскости (DC
), к грани куба (DDC
).Эти ребра — AD, A1D1, BC, B1C1
Закончите предложение, чтобы получилось верное утверждение.
- Две прямые называются перпендикулярными, если …..
- Если плоскости перпендикулярна одной из двух параллельных прямых, то она ……
- параллельны
- один
- она перпендикулярна к любой прямой, лежай в этой плоскости.
- перпендикулярна плоскости.
Правильный вариант/варианты (или правильные комбинации вариантов):
Две прямые называются перпендикулярными, если …
угол между ними равен 90
Если плоскость перпендикулярна одной из двух параллельных прямых, то она …
перпендикулярна и другой
Неправильный вариант/варианты (или комбинации):
Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к третьей прямой.
Теорема: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

Лекция по геометрии на тему: «Перпендикулярность в пространстве». 10-й класс
Разделы: Математика
Класс: 10
Тема: Перпендикулярность прямой и плоскости.
Определение: Две прямые в пространстве могут пересекаться. (Привести примеры перпендикулярных прямых, используя окружающую обстановку).
Лемма: Если одна из двух прямых перпендикулярна к третьей прямой, то другая прямая перпендикулярна к этой прямой.
Дано: a || b, a 
Доказать: b 
Через т.М | М 






Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
(Возможна запись: a 


Прямая, перпендикулярная к плоскости пересекает эту плоскость.
a 





Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая также перпендикулярна к этой плоскости.
Дано: a || b, a 
Доказать: b 
Проведем в плоскости 



Теорема (обратная): Если 2 прямые перпендикулярны к плоскости, то они параллельны.
(Доказать предлагается учащимся самостоятельно).
Теорема: Если прямая, не лежащая в плоскости перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то прямая и плоскость перпендикулярны.
Предлагается 2 способа доказательства.
Дано: a 




Доказать: a 
Проведем в плоскости 

































Дано: m



Доказать: l 
Проведем прямую p так, чтобы O 











Замечание: Еще одно доказательство теоремы в учебнике “Геометрия 10-11” Л.С. Атанасяна и др.
Свойства перпендикулярных прямой и плоскости:
 и
и  перпендикулярны к прямой а ,то они параллельны.
перпендикулярны к прямой а ,то они параллельны.Теорема: Через любую точку пространства не принадлежащую плоскости проходит прямая перпендикулярная к данной плоскости, и притом только одна.
Дано: 

Доказать: 


Доказательство:
- Проведем в
произвольную прямую а; построим плоскость
а, проходящую через т.А
=b В плоскости
через А проведем прямую с | c
(c
b по построению c
а, т.к.
). Значит, с и есть искомая прямая.
- Докажем, что она единственная. Допустим, что это не так и существует прямая с1
, тогда с || c1 ,что не возможно т.к. с х с1=А. Таким образом, через А проходит только одна прямая к
. Что и требовалось доказать
Можно предложить учащимся подготовить к семинару ответы на следующие вопросы:
 , а b
, а b 

. Существует ли прямая перпендикулярная к прямым а и b?
Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Лемма о перпендикулярности двух параллельных прямых
Скачать
презентацию
Дано:а llв , а^c Доказать:в ^c. Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой,то и другая прямая перпендикулярна к этой прямой.
Слайд 4 из презентации «Условие перпендикулярности прямой и плоскости». Размер архива с презентацией 415 КБ.
Видео:Перпендикулярность прямых в пространстве. 10 класс.Скачать

Геометрия 10 класс
«Площадь поверхности конуса» — Как вычислить длину окружности. Урок геометрии. Как вычислить длину дуги. Площадь полной поверхности конуса. Развёртка боковой поверхности конуса. Площадь развёртки. Изготовьте развёртку боковой поверхности конуса. Выполните вычисления. Модель конуса. Радиус основания конуса. Площади поверхностей двух конусов. Вычислите площадь. Найденное выражение. Площадь поверхности конуса. Вывод формулы. Положительные числа.
«Определение двугранных углов» — Теорема трёх перпендикуляров. Ромб. Грани параллелепипеда. Построение линейного угла. Построим BK. Данная пирамида. Свойства. Точка К удалена от каждой стороны. Концы отрезка. Точка на ребре может быть произвольная. Определение и свойства. Точка К. Перпендикуляр , наклонная и проекция. Точка А. Задача. Где можно увидеть теорему трёх перпендикуляров. Основание пирамиды. Перпендикулярные плоскости. Фигура, образованная прямой а и двумя полуплоскостями.
«Следствия из аксиом стереометрии» — Аксиомы стереометрии и некоторые следствия из них. Аксиомы стереометрии. Объяснение нового материала. Стереометрия. Планиметрия. Опрос домашнего задания. Проведите прямую. Раздел геометрии. Аксиомы планиметрии. Плоскость и прямая. Постройте изображение куба. Слайды по геометрии. Пересечение прямой с плоскостью. Решение. Самостоятельная работа. Найдите прямую пересечения плоскостей. Элементы куба. Различные прямые.
«Двугранный угол, перпендикулярность плоскостей» — Признак перпендикулярности двух плоскостей. Найдите тангенс угла. Планиметрия. Перпендикулярность плоскостей. Сечение. Диагональ. Плоскость и не лежащая в ней прямая. Плоскости стены и пола. Линейный угол двугранного угла. Четырехугольник. Квадрат диагонали прямоугольного параллелепипеда. Диагональ куба. Расстояние между скрещивающимися прямыми. Найдите угол. Все шесть граней – прямоугольники. Двугранные углы.
«Примеры симметрии в природе» — Виды симметрии. Симметрия в географии. Примеры симметричного распределения. Симметрия в геологии. Симметрия в биологии. Природные объекты. Симметричные фигуры. Что такое симметрия. Симметрия является фундаментальным свойством природы. Человек, многие животные и растения обладают двусторонней симметрией. Симметрия в природе. Симметрия в физике. Симметрия цилиндра. Симметрия внешней формы кристалла.
«Введение в стереометрию» — Плоскость. Подведение итогов урока. Стереометрия -. Фигуры. Кроссворд. Геометрические знания применялись. Мобильные жилища индейцев называются Типи. Возьмём 6 спичек. Журнал «Квант». Тела. Школьная геометрия. Планиметрия. Арифметика. Многогранник. Переведем на язык площадей. Геометрические знания помогали.
Всего в теме «Геометрия 10 класс» 54 презентации
🎥 Видео
Параллельные прямые | Математика | TutorOnlineСкачать

10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Параллельность прямых. 10 класс.Скачать

Геометрия 10 класс (Урок№9 - Признак перпендикулярности прямой и плоскости.)Скачать

Геометрия 10 класс (Урок№8 - Перпендикулярность прямой и плоскости.)Скачать

10 класс, 23 урок, Признак перпендикулярности двух плоскостейСкачать

10 класс, 18 урок, Теорема о прямой, перпендикулярной к плоскостиСкачать

Геометрия. 7 класс. Теоремы. Т2. Теорема о двух прямых, перпендикулярных к третьей.Скачать

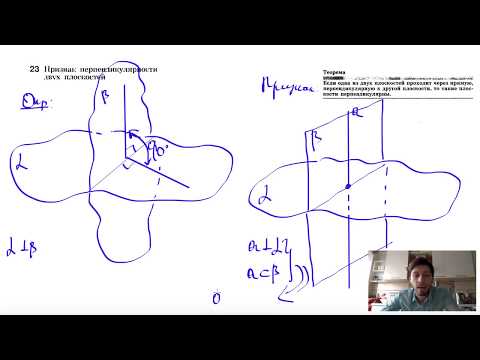
23. Признак перпендикулярности двух плоскостейСкачать
Доказательство 2 и 3 признаков параллельности прямых.Скачать

Теорема о трех перпендикулярах. Теория.Скачать

5. Параллельность трех прямыхСкачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Теорема 13.2 Если две прямые параллельны третьей, то они параллельны ||Геометрия 7 класс||Скачать

10 класс, 15 урок, Перпендикулярные прямые в пространствеСкачать









 ), к грани куба (DDC
), к грани куба (DDC ).Эти ребра — AD, A1D1, BC, B1C1
).Эти ребра — AD, A1D1, BC, B1C1












