 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
Рис.1 Инверсор Липкина-Поселье Рис.2. Инверсор Гарта
На лекции, используя свойства преобразования инверсии, объясняется работа инверсоров Липкина – Поселье и Гарта.
Дальнейшие исследования в этом направлении, которые завершил англичанин Альфред Кемпе, показали, что любая алгебраическая кривая ( F ( x , y ) =0, F –полином от двух переменных) может быть теоретически точно начерчена с помощью некоторого шарнирного механизма . Можно построить, тем самым, шарнирные механизмы, которые будут рисовать параболы, гиперболы, эллипсы. Это, конечно, очень красивая и важная теорема. Правда, если взглянуть на эту теорему глазами практика, пожелавшего построить своими руками шарнирный механизм даже для какой-нибудь простой кривой, то он оказывается очень громоздким – при его помощи трудно чертить, а сделать «в материале» еще труднее. В современной теории при разработке деталей машин и конструировании роботов, манипуляторов и т. д. приходится использовать уже не только такие прямолинейные шарнирные механизмы, а более замысловатые; но классические корни и основы этой теории как раз и обсуждаются на лекции.
К вопросу о шарнирных механизмах мы возвращаемся в курсе анализа при изучении кривых Уатта, их классификации и задачи Чебышева о наилучшем приближении функций алгебраическими многочленами.
По итогам проводится к оллоквиум по теме «Инверсия»
1. Г. , , Новые встречи с геометрией. –М.: Наука 1978.
2. Р. Курант, Г. Роббинс, Что такое математика? – М.: МЦНМО, 2001.
3. , Шарнирные механизмы. Кривые Уатта. – Журнал «Квант», 1(1977).
4. – архитектор и строитель математического знания. – Журнал «Потенциал», 6(2007),
Лекция 19. Задача Аполлония
Рассматривается один из классических примеров применения преобразования инверсии.
Задача Аполлония. Построить (при помощи циркуля и линейки) окружность, касающуюся трех данных окружностей.
Изложение традиционно ….. и на лекции рассматривается сразу все случаи, когда хотя бы две окружности касаются друг друга (внутренним или внешним образом).
Поскольку мы причисляем к окружностям и точки и прямые, то общая задача Аполлония позволяет построить окружность или прямую, касающуюся:
1) трех данных окружностей;
2) данной прямой и двух данных окружностей;
3) двух данных прямых и данной окружности;
4) трех данных прямых;
5) данной точки и двух данных окружностей;
6) данной точки, данной прямой и данной окружности;
7) данной точки и двух данных прямых;
8) двух данных точек и данной окружности;
9) двух данных точек и данной прямой;
10) трех данных точек.
Все перечисленные задачи на построения подробно обсуждаются на упражнениях. Обращается внимание на одну задачу (см…..) и возможные ее варианты обобщения (в частности, для подготовки докладов для участия в научных конференциях школьников).
Замечание . Аполлоний (ок.262-190 г. г. до н. э.) родился в г. Перга – одной из колоний Греции в Малой Азии. Долгое время работал в Александрии. Его главное сочинение (в восьми книгах) называется «О конических сечениях». Метод, который он применял в этом сочинении привел позднее Декарта и Ферма к созданию аналитической геометрии. Ввел многие термины: асимптота, абсцисса, ордината, аппликата.
1. , Инверсия и задача Аполлония. –Журнал «Квант», 8(1971).
2. , Аполлоний Пергский. — — М.: МЦНМО, 2004.
3. , , Геометрические свойства кривых второго порядка. –М.:МЦНМО, 2007.
Лекция 20. Прямая Эйлера
Доказательство основного здесь результата основано на двух леммах.
Лемма 1. Пусть АВС – треугольник; О – его центр описанной окружности; Н – ортоцентр. Тогда угол АВО равен углу НВС (аналогично равны углы ВАО и САН; ВНС и АСО).
Лемма 2. Расстояние от вершины треугольника до ортоцентра равно 2 R , умноженное на модуль косинуса угла в этой вершине.
Теорема Эйлера. Пусть АВС – треугольник, Н – его ортоцентр, О – центр описанной окружности, G – барицентр. Точки H , G , O лежат на одной прямой, причем HG : GO =2:1 (эта прямая называется «прямой Эйлера»).
Замечание. Основной конструкцией здесь является рисунок, который получается после продолжения высоты, медианы и биссектрисы одного угла до пересечения с описанной окружностью данного треугольника.
Дополнительно рассматриваются некоторые задачи (отвечающие теме) на построение при помощи циркуля и линейки. В качестве примера приведем результат, который появился сначала в качестве одного из вопросов на уроках, а затем вылился в самостоятельную исследовательскую работу учащихся.
Теорема («о Н2О») Множество всех точек плоскости π, где могут находиться вершины треугольников (рис.1) представляет из себя плоскость, из которой удалены окружность Г1 без Н с диаметром Н G и внутренность круга с диаметром GH 1 , где Н – такая точка плоскости, что 2О G = GH (ортоцентр треугольника), а Н1 – точка, симметричная Н относительно О. При этом (А – одна из вершин треугольника, G – его центр тяжести, О – центр описанной окружности, Г3 – окружность с диаметром НН1):
1. Если А принадлежит Г3, то треугольник – прямоугольный.
2. Если А расположена внутри Г3, но вне Г1 и «запретной зоны», то
треугольник – тупоугольный и А – острый.
3. Если А расположена внутри Г1, то треугольник – тупоугольный, А – тупой.
4. Если А расположена вне Г3, то треугольник остроугольный.
1. Г. , , Новые встречи с геометрией. –М.: Наука 1978.
2. Р. Курант, Г. Роббинс, Что такое математика? – М.: МЦНМО, 2001.
3. , Избранные лекции по геометрии. – Алматы, Дарын, 1999.
Лекция 21. Проективные теоремы Паппа и Брианшона
Целью этой лекции является знакомство с двумя классическими теоремами проективного характера.
Теорема Паппа. Если вершины шестиугольника лежат поочередно на двух пересекающихся прямых, то точки пересечения их противоположных прямых лежат на одной прямой.
Теорема Брианшона. Если стороны шестиугольника проходят поочередно через две данные точки, то три диагонали, соединяющие противоположные вершины шестиугольника, кокуррентны.
Сходство этих теорем бросается в глаза, если обе теоремы выписать рядом на доске, разделив ее на две части. Проводя такой анализ, указывается на общий принцип двойственности.
Внутренняя причина принципа двойственности (а не прямые доказательства двойственных теорем) в проективной плоскости устанавливается нами позже.
На лекциях и на семинарских занятиях учащимся сообщаются сведения исторического характера. Отметим здесь особо, что Блез Паскаль () доказал свою теорему «о мистическом шестиугольнике» в возрасте 16 лет.
1. Р. Курант, Г. Роббинс, Что такое математика? – М.: МЦНМО, 2001.
2. , Проективная геометрия в задачах. – М.: Физматгиз, 1954.
Лекция 22. Теорема Евклида о трех параллелограммах
Медиана А D треугольника АВС делит его на два равновеликих по площади треугольника. Кроме того, отметим, что точка Р внутри треугольника АВС принадлежит медиане треугольника, тогда и только тогда, когда [ВАР] = [САР]; здесь и всюду в дальнейшем [ F ] обозначает площадь F .
Рассмотрим теперь параллелограмм и точку Р внутри него. Проведем через Р прямые KL и MN , параллельные соответственно сторонам AD и AB параллелограмма ABCD . Тогда, если точка Р расположена на диагонали АС этого параллелограмма, то [ PMDL ] = [ PKBN ]. Это равенство площадей является следствием того, что диагональ параллелограмма делит его на два равновеликих по площади треугольника.
Теорема 1 . (О мотыльке). Пусть Р — точка внутри параллелограмма и через нее проведены прямые, параллельные его сторонам, которые делят его на четыре других параллелограмма. Точка Р принадлежит диагонали исходного параллелограмма тогда и только тогда когда равновелики два из четырех указанных параллелограммов, расположенных по разные стороны от нее.
Важным дополнением к теореме о мотыльке является следующий классический результат.
Теорема 2 (Евклид). Пусть Р — произвольная точка внутри параллелограмма АВС D , через которую проведены прямые KL и MN , параллельные сторонам параллелограмма (рис.5). Тогда прямые DK , BM и CP (диагонали трех параллелограммов или их продолжений) пересекаются в одной точке.
Замечание 1. Теорема 2, конечно, остается справедливой, если мы выбираем три параллелограмма, о которых идет речь, и другим образом. (А сколько всего различных случаев имеется?) При выборе таких параллелограммов нужно лишь позаботиться о том, чтобы любая пара из них имела ровно одну общую вершину. А это можно обеспечить так: выберем из девяти точек пересечения двух троек параллельных между собой прямых три точки так, чтобы на каждой прямой была выбрана ровно одна точка. Любой выбор такой тройки точек и задает те общие вершины у нужных параллелограммов (стороны треугольника, показанные на рис.1, с вершинами в таких точках, являются другими диагоналями выбираемой тройки параллелограммов, а не тех диагоналей, о которых идет речь в теореме).
Простым следствием теоремы о трех параллелограммах является еще одна классическая теорема.
Теорема 3 (Прямая Гаусса для четырехугольника). Если противоположные стороны AB , CD и AD , BC четырехугольника ABCD пересекаются (при продолжении) в точках X и Y , то середины его диагоналей AC , BD и середина отрезка XY принадлежат одной прямой.
Вернемся к теореме о трех параллелограммах. В этой теореме речь идет о том, что три прямые пересекаются в одной точке. Другими словами, она носит «проективный характер». А что понимается под этим?
Представим себе, что одну из возможных картинок, показанных на рис.1, при помощи параллельной проекции мы спроектировали на какую-то другую плоскость (тень рисунка от пучка параллельных лучей). Параллельная проекция прямой есть прямая (если только эта прямая не параллельна направлению проекции) и, кроме того, параллельная проекция сохраняет параллельность прямых. С другой стороны, величины углов, параллельная проекция, вообще говоря, не сохраняет. Поэтому, чтобы доказать теорему о трех параллелограммах можно решить задачу сначала для прямоугольников. Затем нужно будет только показать, что рисунок из теоремы о трех параллелограммов можно получить из рисунка для трех прямоугольников при помощи некоторой параллельной проекции. Попробуйте самостоятельно доказать, что такая процедура всегда возможна.
Кроме параллельной проекции имеется еще и центральная проекция (как при фотографировании), когда пучок параллельных прямых заменяется пучком прямых, проходящих через одну точку («тень» от пучка лучей от точечного источника света). Центральная проекция сохраняет факт о принадлежности трех точек одной прямой, но, вообще говоря, не сохраняет свойство параллельности прямых. Например, если расположить нужный рисунок на одной грани прозрачного параллелепипеда и выбрать центр проекции как показано на рис. 2, то на плоскости, которая содержит основание параллелепипеда, мы получим «тень» рисунка с боковой грани (Объясните построение этой «тени»)
Наличие такой проекции показывает, что верна такая теорема: Если три прямые, имеющие одну общую точку О1 , пересекаются тремя параллельными прямыми (рис. 3), то три выделенные на рисунке прямые пересекаются в одной точке.
Поместим теперь рис.3 на боковую грань параллелепипеда и посмотрим на его «тень» после центральной проекции из центра О2. Ясно, что на плоскости содержащей нижнюю грань параллелепипеда мы получим «тень», похожую на рис.4.
Мы не будем здесь точно формулировать полученный результат. Отметим лишь, что перевоплощения параллелограммов после двух центральных проекций привели нас к довольно общей теореме о точках пересечения двух троек прямых (каждая тройка имеет общую точку), где никаких параллельностей нет.
Мы только чуть-чуть прикоснулись к теоремам проективного характера. Изучением свойств фигур, которые не меняются после конечного числа центральных проекций – это предмет так называемой проективной геометрии.
1. Евклид, Начала. Кн. I — YI . –М.-Л.: Гостехиздат, 1948.
2. , Проективная геометрия в задачах. – М.: Физматгиз, 1954.
3. , Геометрические метаморфозы. — Журнал «Квант», 6(1997).
Лекция 23. Построения одной линейкой и задачи Штейнера
Задачи на построение при помощи только линейки заимствованы из одной работы Я. Штейнера, в которой им было установлено, что если на плоскости задан круг с его центром, то все построения при помощи циркуля и линейки могут быть реализованы только линейкой. По этому поводу см. [1].
Задачи на построение, которые рассматриваются (на лекциях и упражнениях):
1. а) На прямой р заданы три такие точки А, В,С, что С есть середина отрезка АВ. Построить прямую, параллельную р и проходящую через заданную точку Х.
б) Даны две различные параллельные прямые. Разделить отрезок пополам, который расположен на одной из этих прямых.
в) Через данную точку провести прямую параллельную двум различным параллельным прямым.
г) Разделить отрезок АВ на n равных частей, если задана прямая, параллельная АВ.
2. Дан параллелограмм.
а) Через данную точку провести прямую, параллельную данной прямой.
б) Увеличить данный отрезок в n раз.
в) Разделить данный отрезок на n равных частей.
3. Дан неподвижный круг с центром.
а) Провести через данную точку прямую, параллельную данной прямой.
б) Увеличить (уменьшить) данный отрезок в n раз.
в) Провести через данную точку перпендикуляр к данной прямой.
4. Две данные прямые пересекаются в точке А за пределами чертежа. Постройте прямую, соединяющую данную точку В с точкой А.
5. Провести прямую через данные точки, между которыми расстояние больше, чем длина линейки.
6. На плоскости дан отрезок АВ и область F . Желательно продолжить прямую АВ за область F . Как это можно сделать одной линейкой, чтобы в процессе построения не перекрывать линейкой никакой части области F ?
7. Одна пара прямых пересекается в точке А, а другая пара – в точке В; обе точки А и В находятся за пределами чертежа. Построить ту часть прямой АВ, которая находится в пределах чертежа.
На упражнениях рассматриваются также задачи, связанные с построениями одной двусторонней линейкой.
1. Р. Курант, Г. Роббинс, Что такое математика? – М.: МЦНМО, 2001.
2. Ж. Адамар, Элементарная геометрия. Часть1: Планиметрия. — М.: Просвещение, 1957.
3. , , Геометрические построения на плоскости. –М.: Учпедгиз, 1957.
4. , Проективная геометрия. –М.: Гос. изд-во ИЛ, 1949.
Лекция 24. Лемма Архимеда и площадь треугольника
Лемма Архимеда . Пусть D – середина дуги АС окружности и В некоторая точка этой дуги. Тогда основание Е перпендикуляра, опущенного из точки D на ломаную АВС, делит эту ломаную пополам.
Одно из доказательств в пересказе арабского математика аль — Беруни (гг.) содержится в [2]. Мы приводим другое доказательство.
Архимед на три века раньше Герона Александрийского (жившего, вероятно, в I веке) получил формулу для площади треугольника АВС через длины его сторон a , b , c :
[ABC] =
При выводе этой формулы для площади треугольника Архимед, используя свою лемму, показал, что площадь заданного треугольника равна разности площадей двух подобных равнобедренных треугольников (тесно связанных с исходным); подробности см. в [2].
1. Архимед, Сочинения. –М.: Физматгиз, 1962.
2. , Геометрические задачи древнего мира. –М.: ФАЗИС, 1997. (Библиотека «Ступени знаний, серия «Математика»).
Лекция 25. Парабола и касательная
Пусть на плоскости заданы точка F и прямая d . Параболой ( F ; d ) называется множество точек плоскости P , равноудаленных от точки F и прямой d ; при этом, F называется фокусом параболы, а d — ее директрисой.
Для построения точек параболы проведем окружность радиуса r с центром в фокусе F и прямую, параллельную директрисе d на расстоянии r от неё; если эта прямая пересекает окружность, то точки пересечения принадлежат параболе. Отсюда, в частности, следует, что парабола симметрична относительно прямой, проходящей через точку F и перпендикулярна прямой d ; ось симметрии будем обозначать через l .
Вершина параболы – точка пересечения параболы с ее осью симметрии.
Параболический сегмент — фигура, граница которой состоит их дуги параболы и стягивающей ее хорды.
Устанавливаются следующие свойства:
1 . Парабола делит плоскость на две области: расстояние от любой точки первой области до фокуса параболы меньше расстояния от этой точки до директрисы параболы (внутренность параболы), а для второй области (внешность параболы) указанные расстояния связаны противоположным неравенством.
2 . Для произвольной точки Р параболы ( F ; d ) через P ’ обозначим (здесь и всюду в дальнейшем) точку пересечения директрисы d с прямой, содержащей точку Р и параллельной оси симметрии параболы.
Касательной к параболе ( F ; d ) в ее точке Р назовем серединный перпендикуляр отрезка РР’(медиатрису отрезка РР’).
а) Касательная к параболе имеет с ней только одну общую точку.
б) Для любой точки Р параболы касательная в ее вершине пересекает касательную к параболе в точке Р в середине отрезка FP ’.
в) (Оптическое свойство параболы). Пусть прямая, параллельная оси параболы пересекает ее в точке Р и t – касательная в этой точке. Тогда прямые FP и PP ’ образуют равные углы с касательной t .
3. Прямая, перпендикулярная касательной t к параболе в точке Р, называется нормалью к параболе (обозначим через n ) в ее точке Р.
Для параболы ( F , d ) и ее точки Р через S и Q обозначим соответственно точки пересечения нормали n и касательной t (обе в точке Р) с осью параболы l ; пусть Т обозначает точку пересечения прямой, проходящей через Р и параллельной директрисе d с ее осью симметрии l . Тогда
а) ST = FF ’ и QF = FS ;
б) четырехугольник QFPP ’ — параллелограмм.
4. Пусть А и В две точки параболы ( F , d ) и касательные к параболе в этих точках пересекаются в точке S . Тогда S — центр описанной окружности треугольника A ’ B ’ F .
Видео:Лемма АрхимедаСкачать

Математика. Леммы Архимеда, доказательство + задачи. Теорема Фейрбаха.
Лемма Архимеда
Пусть прямая пересекает данную окружность в точках K и M. Рассмотрим произвольную окружность, касающуюся данной в точке P, а прямой KM в точке L. Тогда прямая PL проходит через середину одной из двух дуг KM, на которые данная окружность разделена прямой KM.
Доказательство: Рассмотрим для определенности случай, изображенный на рисунке. Пусть О – центр данной окружности О1 – центр построенной окружности. Точки О, О1 и Р лежат на одной прямой. Пусть прямая РL пересекает данную окружность в точке Е. Треугольники РО1L и РОЕ равнобедренные. У них есть общий угол – угол при вершине Р.Значит, они подобны, и О1L параллельна ОЕ. Но O1L перпендикулярна КМ. Следовательно, ОЕ также перпендикулярна КМ. Значит, Е – середина дуги. Лемма доказана
Приведем еще одно доказательство леммы Архимеда. Рассмотрим прямую, касающуюся обеих окружностей в точке Р. Обозначим через Q точку её пересечения с прямой КМ; Е – точка пересечения PL с большей окружностью. Углы PLM и QPL равны, так как PQ = LQ как касательные. Но угол PLM измеряется полусуммой дуг КЕ и РМ, а угол QPL = углу QPE и измеряется половиной дуги РМЕ или полусуммой дуг РМ и МЕ. Значит, дуги КЕ и МЕ равны.
Решение Архимеда
Рассмотрим окружность, касающуюся BD то точке L, дуги AD – в точке Р и полуокружности AB — в точке F. Согласно лемме, прямая PL проходит через точку С, а прямая GL – через А. Проведем через L в посторонней окружности диаметр LN. Углы NPL и APC – прямые (как опирающиеся на диаметры в соответствующей окружности), поэтому точки P,N и A лежат на одной прямой. Точно так же на одной прямой лежат точки N,F и B. (Прямые являются углы NFL и AFB.)Обозначим теперь через G точку пересечения AL с большей полуокружностью. Рассмотрим треугольник ALC. Высотами в нем являются LB, AP и CG.
Продолжим их до пересечения в одной точке, которую обозначим через S. Из подобия треугольников SNL и SAB получаем. Но прямые NB и SC параллельны, так как они перпендикулярны AL. Cледует, что NL , при этом NL — диаметр одной из окружностей, вписанных в части арбелоса. Понятно, что находя диаметр второй окружности, мы придем к тому же равенству.
Видео:Лемма Архимеда. Лемма Варьера. Геометрия для олимпиадСкачать

Задача Архимеда об арбелосе
Возможно, на фоне удивительных достижений науки и техники, с которыми вы встречаетесь буквально на каждом шагу, геометрия может показаться каким – то малосовременным, неразвивающимся предметом, не нужным современному человеку, в чью жизнь прочно вошли компьютеры, авиалайнеры,iPhonы, iPodы, лазеры и многое, многое другое.
Да, в целом человечество за свою долгую жизнь стало намного умнее и совершеннее. А вот стал ли умнее и совершеннее сам человек? Сегодня мы знаем больше своих предков потому, что «стоим на их плечах».
Развитие человечества – это, прежде всего, развитие человеческой мысли. И история геометрии является своего рода зеркалом истории этого развития, удивительной сокровищницей, хранящей высшие достижения человеческого гения, жемчужины которой создавались величайшими мыслителями.
Кто не слышал об удивительном ученом Древней Греции Архимеде! Этот великий человек жил в III столетии до н. э. в городе Сиракузы на Сицилии, бывшим в то время греческой колонией. Много прекрасных открытий и изобретений сделал Архимед за свою долгую жизнь. Будучи уже зрелым ученым, в 50 лет, он увлекся геометрией и не расставался с ней до конца своих дней. Говорят, что последними словами Архимеда перед тем, как его убил римский легионер, были: «Осторожно, не наступи на мои круги».
В своих занятиях геометрией Архимед много внимания уделял изучению свойств фигуры, носящей название арбелос, или скорняжный нож. Это название фигура получила из– за сходства с очертаниями ножа, использовавшегося скорняками для разделки кожи.
Если взять на прямой три последовательные точки A, B и C и построить три полуокружности с диаметрами AB, BC, AC, расположенные по одну сторону от прямой, то фигура, ограниченная этими полуокружностями, и является арбелосом.
Видео:Задача №16. Пересекающиеся и касающиеся окружности.Скачать

Задача Архимеда
Проведем в арбелосе через точку B прямую, перпендикулярную AC, и обозначим её точку пересечения с большей полуокружностью через D. Рассмотрим две окружности, вписанные в два образовавшихся криволинейных треугольника. Первая касается отрезка BD, полуокружности AB и дуги DА. Вторая касается отрезка BD, полуокружности ВС и дуги DС. Докажите, что эти две вписанные окружности равны.
Решение Архимеда опиралось на одно простое свойство касающихся окружностей, которое мы назовем леммой Архимеда.
Видео:Лемма Архимеда в задаче с очного тура олимпиады Физтех 2022Скачать

Лемма Архимеда
Пусть прямая пересекает данную окружность в точках K и M. Рассмотрим произвольную окружность, касающуюся данной в точке P, а прямой KM в точке L. Тогда прямая PL проходит через середину одной из двух дуг KM, на которые данная окружность разделена прямой KM.
Доказательство: Рассмотрим для определенности случай, изображенный на рисунке. Пусть О – центр данной окружности О1 – центр построенной окружности. Точки О, О1 и Р лежат на одной прямой. Пусть прямая РL пересекает данную окружность в точке Е. Треугольники РО1L и РОЕ равнобедренные. У них есть общий угол – угол при вершине Р.Значит, они подобны, и О1L параллельна ОЕ. Но O1L перпендикулярна КМ. Следовательно, ОЕ также перпендикулярна КМ. Значит, Е – середина дуги. Лемма доказана
Приведем еще одно доказательство леммы Архимеда. Рассмотрим прямую, касающуюся обеих окружностей в точке Р. Обозначим через Q точку её пересечения с прямой КМ; Е – точка пересечения PL с большей окружностью. Углы PLM и QPL равны, так как PQ = LQ как касательные. Но угол PLM измеряется полусуммой дуг КЕ и РМ, а угол QPL = углу QPE и измеряется половиной дуги РМЕ или полусуммой дуг РМ и МЕ. Значит, дуги КЕ и МЕ равны.
Видео:СЕКРЕТНАЯ "Лемма 255" в №16 из ЕГЭ 2020 по профильной МАТЕМАТИКЕСкачать

Решение Архимеда
Рассмотрим окружность, касающуюся BD то точке L, дуги AD – в точке Р и полуокружности AB — в точке F. Согласно лемме, прямая PL проходит через точку С, а прямая GL – через А. Проведем через L в посторонней окружности диаметр LN. Углы NPL и APC – прямые (как опирающиеся на диаметры в соответствующей окружности), поэтому точки P,N и A лежат на одной прямой. Точно так же на одной прямой лежат точки N,F и B. (Прямые являются углы NFL и AFB.)Обозначим теперь через G точку пересечения AL с большей полуокружностью. Рассмотрим треугольник ALC. Высотами в нем являются LB, AP и CG. Продолжим их до пересечения в одной точке, которую обозначим через S. Из подобия треугольников SNL и SAB получаем. Но прямые NB и SC параллельны, так как они перпендикулярны AL. Cледует, что NL , при этом NL — диаметр одной из окружностей, вписанных в части арбелоса. Понятно, что находя диаметр второй окружности, мы придем к тому же равенству.
📽️ Видео
Один день с МО и планиметрией. Убийство №16 леммой Архимеда. ЕГЭ2021Скачать

9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Лемма АрхимедаСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

01.10.2022 Лекция 6. Принцип Архимеда. Теорема Кантора, лемма Бореля-ЛебегаСкачать

Поступайте правильно Математика ЕГЭСкачать
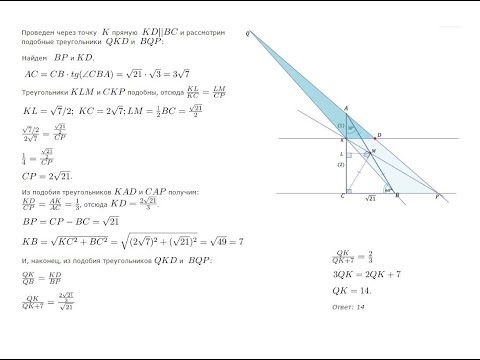
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Касание окружностей | Задачи 11-15 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Задание 24 Две пересекающиеся окружностиСкачать
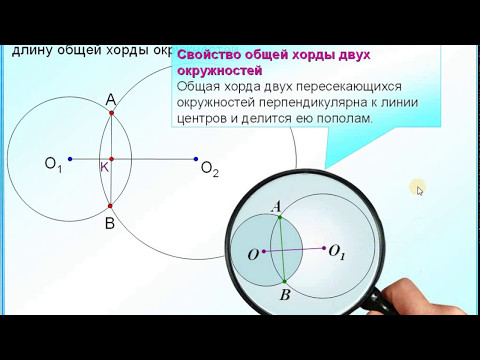
КАСАЮЩИЕСЯ ОКРУЖНОСТИСкачать

25.09.2021 Лекция 6. Принцип Архимеда и его следствия, теорема Кантора, лемма Бореля-ЛебегаСкачать

#7str. Как использовать инверсию?Скачать

Лекальные кривые. Спираль Архимеда. Эвольвента окружности. ЦиклоидаСкачать

Инверсия и арбелос АрхимедаСкачать

Матанализ. Лекция 1. Аксиома Архимеда, сечения ДедекиндаСкачать










