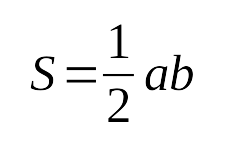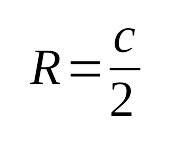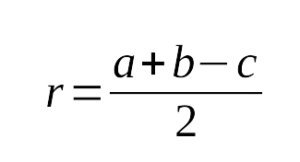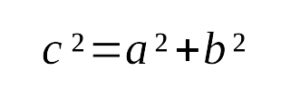Квадрат вписан в треугольник свойства

Видео:Решали пол-урока, а оказалось очень простоСкачать

Определение

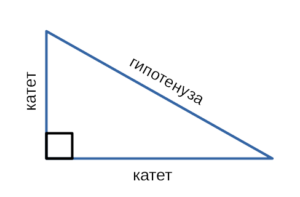
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.

Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.

Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.

Видео:✓ Квадрат вписан в прямоугольный треугольник | Ботай со мной #129 | Борис ТрушинСкачать

Свойства прямоугольного треугольника

В прямоугольном треугольнике:

1. Сумма острых углов 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
3. Медиана, проведенная к гипотенузе, равна ее половине.
4. Центр описанной окружности — середина гипотенузы.
   

Формулы:

1. Площадь прямоугольного треугольника равна
   половине произведения катетов:
   
2. Радиус описанной окружности около прямоугольного
   треугольника равен половине гипотенузы:
   
3. Радиус вписанной окружности в прямоугольный треугольник
   выражается следующим образом:
   
4. Квадрат гипотенузы равен сумме квадратов катетов:

Видео:Задача про квадрат в треугольнике и 2 способа её решения: с помощью геометрии и с помощью логикиСкачать

Признаки равенства прямоугольных треугольников

С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.

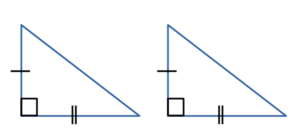
1. По двум катетам:
   Если два катета одного прямоугольного треугольника соответственно
   равны двум катетам другого прямоугольного треугольника,
   то такие треугольники равны.
   
2. По катету и гипотенузе:
   Если катет и гипотенуза одного прямоугольного треугольника соответственно
   равны катету и гипотенузе другого прямоугольного треугольника,
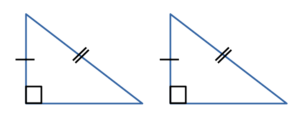
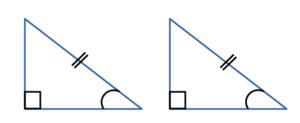
   то такие треугольники равны.
   
3. По гипотенузе и острому углу:
   Если гипотенуза и острый угол одного прямоугольного треугольника соответственно
   равны гипотенузе и острому углу другого прямоугольного треугольника,
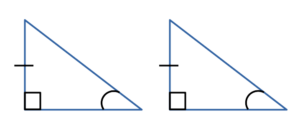
   то такие треугольникиравны.
   
4. По катету и острому углу:
   Если катет и острый угол одного прямоугольного треугольника соответственно
   равны катету и острому углу другого прямоугольного треугольника,
   то такие треугольники равны.

Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Признаки прямоугольного треугольника

С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.

1. По теореме Пифагора:
   Если квадрат стороны равен сумме квадратов двух других сторон,
   то треугольник прямоугольный.
2. По центру описанной окружности:
   Если центр описанной окружности лежит на стороне треугольника,
   то треугольник прямоугольный.
3. По медиане:
   Если медиана треугольника равна половине стороны, к которой она проведена,
   то треугольник прямоугольный.
4. По площади:
   Если площадь треугольника равна половине произведения двух его сторон,
   то треугольник прямоугольный.
5. По радиусу описанной окружности:
   Если радиус описанной окружности равен половине,
   то треугольник прямоугольный.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Признаки подобия прямоугольных треугольников

С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Please wait.

Видео:Сможешь найти площадь квадрата? Задача про квадрат, вписанный в прямоугольный треугольникСкачать

We are checking your browser. mathvox.ru

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d9f2e4a2e1876ad • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Видео:Геометрия В правильный треугольник вписан квадрат, сторона которого равна m. Найти стонуСкачать

Прямоугольный треугольник. Теорема Пифагора.

теория по математике 📈 планиметрия

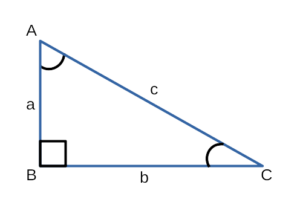
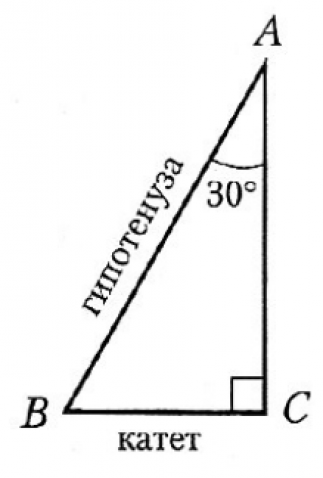
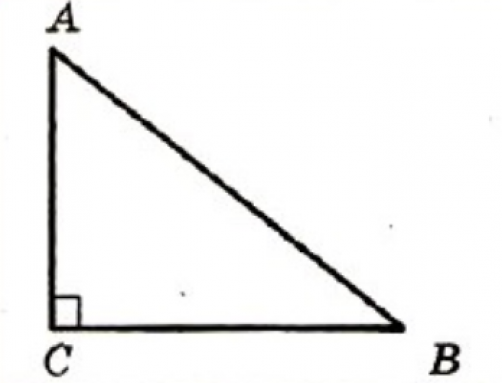
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

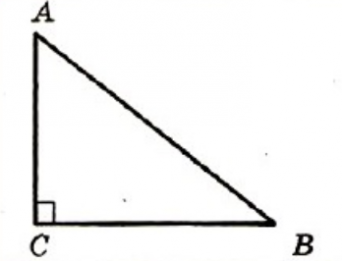
На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Свойства прямоугольного треугольника

• В прямоугольном треугольнике гипотенуза является наибольшей стороной.
• В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .

Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .

• Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
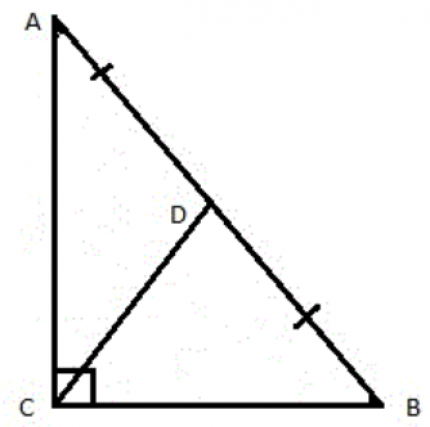
• Медиана, проведенная к гипотенузе, равна её половине.

На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Видео:Геометрия В прямоугольный треугольник с катетами a и b вписан квадрат, имеющий с треугольником общийСкачать

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

1. по катетам;
2. по катету и прилежащему острому углу;
3. по гипотенузе и острому углу;
4. по гипотенузе и катету.

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.

💡 Видео

Нужно найти площадь большого квадратаСкачать

Найдите площадь правильного треугольника внутри квадратаСкачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Задание 26 Вписанный квадратСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Геометрия В треугольник ABC вписан квадрат так, что две его соседние вершины принадлежат стороне ACСкачать

Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать