Квадрат с вершинами на осях окружности как построить

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Техническое черчение

Popular

Основы черчения

Строительное

Машиностроительное

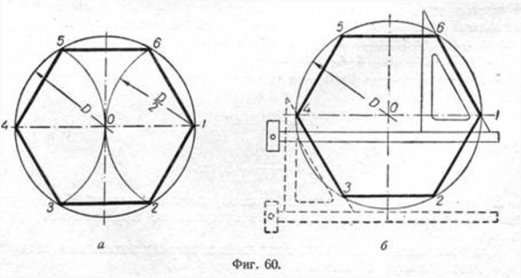
Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

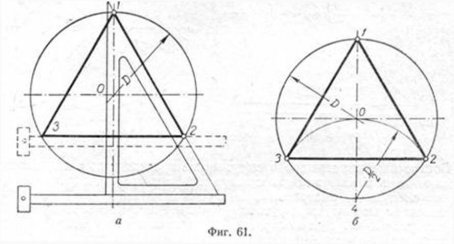
Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

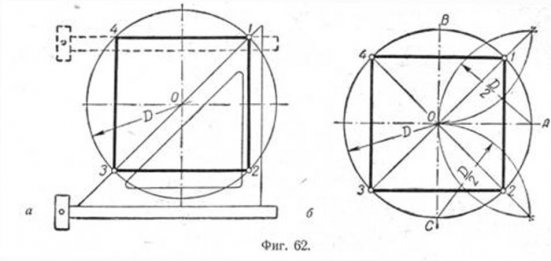
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

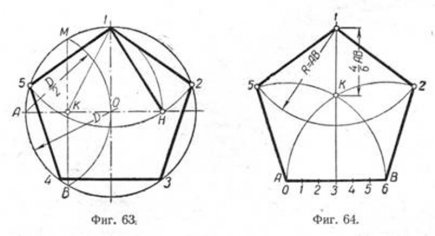
Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

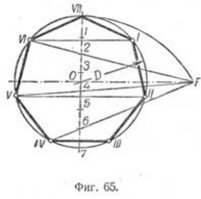
Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

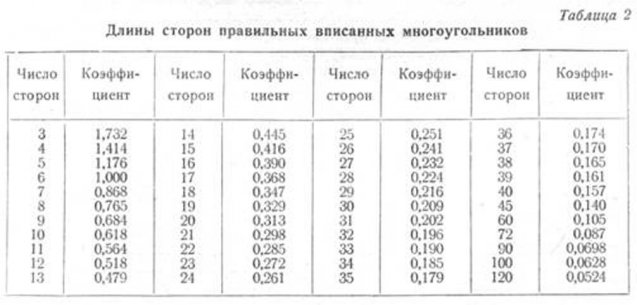
Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Видео:Как построить квадрат, два способаСкачать

Как построить квадрат в окружности с помощью циркуля?

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Как построить циркулем?

1. Циркулем проводим окружности с центром в точках A и B радиусом AB.
2. Находим точки пересечения P и Q двух построенных окружностей (дуг).
3. По линейке проводим отрезок или линию, проходящую через точки P и Q.
4. Находим искомую середину отрезка AB — точку пересечения AB и PQ.

Видео:Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

Как вычислить квадрат в окружности?

S = 4 × r 2 , где r — это радиус вписанной окружности.

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Как найти диагональ в квадрате?

Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Соответствие круга и квадрата в перспективе.

Анализируя различные положения квадрата и окружности относительно точки зрения и линии горизонта а также правила их изображения в перспективе легко обнаружить общие закономерности. Геометричес­кая связь этих фигур определяется тем, что вокруг любой окружности можно описать квадрат, а также в лю­бой квадрат можно вписать окружность.

Как вписать окружность в квадрат?

Рассмотрите рисунок 48. Квадрат и вписанная в него окружность имеют общий центр — точку пересече­ния диагоналей квадрата. Окружность касается сторон квадрата в точках 1,2,3,4.Точки касания делят стороны квадрата пополам. Для того чтобы изобразить вписанную в квадрат окружность (в перспективном рисунке — эл­липс) необходимо определить положение осей эллипса и найти точки, задающие его размеры (точки 1 — 4).

Горизонтальный квадрат.

Найдите точки касания на перспективном рисунке горизонтально расположенного квадрата (рис.49): для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и ухо­дящие с ними в одну точку схода.

Окружность, лежащая в горизонтальной плоскости, изображается в виде эллипса с вертикальной и го­ризонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллип­са. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения ди­агоналей квадрата (центра окружности) ближе к зрителю (рис.50). Таким образом, мы получили две оси эл­липса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями ка­рандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1,2,3,4. Проверьте симметричность полученного эллипса относительно его осей (рис. 51).

перспективный рисунок простых геометрических тел

Вертикальный квадрат.

При вертикальном положении квадрата точки 1,2,3,4найдите, как и в предыдущем примере: прове­дите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис.52). Несколь­ко сложнее определить направление осей эллипса. Для решения этой задачи представьте, что изображаемый нами эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 53). Ось цилиндра всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось ци­линдра через точку пересечения диагоналей квадрата. Ее направление можно найти, опираясь на знание и опыт рисования куба, или взять с натуры, если таковая имеется. Таким образом, мы определили положение малой оси эллипса. А большая ось будет ей перпендикулярна и пройдет через точку, смещенную от пересе­чения диагоналей — центра окружности — ближе к зрителю (рис.54). На двух осях и по четырем точкам сна­чала наметьте эллипс легкими линиями, а затем уточните рисунок (рис.55).

Заметим, что эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и исправлений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигу­ры, близкие к ним. Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспекти­ве, поэтому задачу грамотного изображения квадрата современная методика рисования предлагает решать с помощью эллипса, вокруг которого описывается квадрат.

Видео:Уравнение окружности (1)Скачать

Перечертите квадрат в тетрадь построй окружность так чтобы все вершины квадрата оказались на окружности обьясни план построения окружности проведи все оси симметрии квадрата является ли они осями симм?

Математика | 1 — 4 классы

Перечертите квадрат в тетрадь построй окружность так чтобы все вершины квадрата оказались на окружности обьясни план построения окружности проведи все оси симметрии квадрата является ли они осями симметрии окружности Поясни свой ответсторона квадрата 4 см.

Вспоминаем, что клетки в тетради по 5 мм или на 1 см нужно 2 клетки.

Осей симметрии у квадрата — четыре — зеленым нарисованы.

Две по середине стороны и две по диагоналям.

Вот и ПРОЩЕ центр окружности найти на пересечении ДИАГОНАЛЕЙ.

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Начертить в тетради квадрат с длиной стороны 3см?

Начертить в тетради квадрат с длиной стороны 3см.

Проведи его оси симметрии.

Сколько осей симметрии у квадрата?

Выбери верный ответ : 2, 4, 6.

Видео:Как построить шестиугольник вписанный в окружностьСкачать

Начерти квадрат с длиной стороны 4см?

Начерти квадрат с длиной стороны 4см.

Чему равна площадь этого квадрата?

Проведи все оси симметрии квадрата.

Сколько осей у тебя получилось?

Видео:Построение 8 угольника циркулемСкачать

Петя говорит, что квадрат это прямоугольник, поэтому диагональ квадрата не является его осью симметрии?

Петя говорит, что квадрат это прямоугольник, поэтому диагональ квадрата не является его осью симметрии.

Поясни свой ответ.

Видео:Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Начерти в тетради окружность, радиус которого равен 3 см?

Начерти в тетради окружность, радиус которого равен 3 см.

Проведи диаметр и построй на нём, как на диагонали, квадрат.

Где будут расположены вершины этого квадрата?

Видео:Изображение в изометрической проекции окружностей, вписанных в кубСкачать

Начерти в тетради квадрат с длиной стороны 3 см ?

Начерти в тетради квадрат с длиной стороны 3 см .

Проведи его оси симметрии.

Сколько осей симметрии у квадрата?

Видео:Как вписать квадрат в окружностьСкачать

Построй квадрат со стороной 4 сантиметра сколько у него осей симметрии произведите их?

Построй квадрат со стороной 4 сантиметра сколько у него осей симметрии произведите их.

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Перечерти квадрат в тетрадь?

Перечерти квадрат в тетрадь.

Построй окружность так, чтобы все вершины квадрата оказались на окружности.

Объясни план построения окружностей.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Построй квадрат со стороной 4 см?

Построй квадрат со стороной 4 см.

Сколько у него осей симметрии?

Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Все ли оси симметрии квадрата проведены?

Все ли оси симметрии квадрата проведены?

Отметь знаком свой ответ.

Видео:Построение пятиугольника циркулемСкачать

Любой квадрат является прямоугольником?

Любой квадрат является прямоугольником.

У квадрата 4 оси симметрии значит у любого прямоугольника тоже 4 оси симметрии верни ли ход рассуждений и вывод ?

Вы открыли страницу вопроса Перечертите квадрат в тетрадь построй окружность так чтобы все вершины квадрата оказались на окружности обьясни план построения окружности проведи все оси симметрии квадрата является ли они осями симм?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 1 — 4 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

1) 14 + 14 + 2 = 30 2)1×43 = 43÷1 3)18 — 18 = 16 — 16 4)0 + 20 = 12 + 8 с первым можно и подругому. Например, 12 + 5 + 13 = 30 или 11 + 11 + 8 = 30, вариантов много. Подписывайся)))♤.

1) x + x + x = 30 ; x = 10 2)x * 43 = 43 : x ; x = 1 3)x — 18 = 16 — 16 ; x = 18 4) x + 20 = 12 + 8 ; x = 0.

Вот так наверное я думаю.

7, 12 * 7, 12 = 50, 7 50. 7 — 0, 6044 = 50, 0956 = 50, 1 a.

Любое однозначное число должно иметь двух соседей c этой же цифрой и среди других однозначных чисел таких соседей, очевидно, нет, т. Е. на круге есть двузначные числа. Значит на круге есть и число 9 и его минимально возможные соседи 19 и 29, откуда..

1)28 : 4 = 7 учеников занимаются спортом 2) 12 : 3 = 4 птицы улетели 12 — 4 = 8 птиц осталось.

— 2•( — 4) + 10•( — 2)•x•y Ну я не уверенна.

— 2х + 8 + 10т — 20 = — 2х + 10т — 12 всееееееееее.

А)245 + 35 * 18 = 5040, б) (87 + 35) * 25 = 3050 , в)10260 : 36 + 164 = 449 прости (г) не смог.

Видео:Математика это не ИсламСкачать

Соответствие круга и квадрата в перспективе.

Анализируя различные положения квадрата и окружности относительно точки зрения и линии горизонта а также правила их изображения в перспективе легко обнаружить общие закономерности. Геометричес­кая связь этих фигур определяется тем, что вокруг любой окружности можно описать квадрат, а также в лю­бой квадрат можно вписать окружность.

Как вписать окружность в квадрат?

Рассмотрите рисунок 48. Квадрат и вписанная в него окружность имеют общий центр — точку пересече­ния диагоналей квадрата. Окружность касается сторон квадрата в точках 1,2,3,4.Точки касания делят стороны квадрата пополам. Для того чтобы изобразить вписанную в квадрат окружность (в перспективном рисунке — эл­липс) необходимо определить положение осей эллипса и найти точки, задающие его размеры (точки 1 — 4).

Горизонтальный квадрат.

Найдите точки касания на перспективном рисунке горизонтально расположенного квадрата (рис.49): для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и ухо­дящие с ними в одну точку схода.

Окружность, лежащая в горизонтальной плоскости, изображается в виде эллипса с вертикальной и го­ризонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллип­са. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения ди­агоналей квадрата (центра окружности) ближе к зрителю (рис.50). Таким образом, мы получили две оси эл­липса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями ка­рандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1,2,3,4. Проверьте симметричность полученного эллипса относительно его осей (рис. 51).

перспективный рисунок простых геометрических тел

Вертикальный квадрат.

При вертикальном положении квадрата точки 1,2,3,4найдите, как и в предыдущем примере: прове­дите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис.52). Несколь­ко сложнее определить направление осей эллипса. Для решения этой задачи представьте, что изображаемый нами эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 53). Ось цилиндра всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось ци­линдра через точку пересечения диагоналей квадрата. Ее направление можно найти, опираясь на знание и опыт рисования куба, или взять с натуры, если таковая имеется. Таким образом, мы определили положение малой оси эллипса. А большая ось будет ей перпендикулярна и пройдет через точку, смещенную от пересе­чения диагоналей — центра окружности — ближе к зрителю (рис.54). На двух осях и по четырем точкам сна­чала наметьте эллипс легкими линиями, а затем уточните рисунок (рис.55).

Заметим, что эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и исправлений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигу­ры, близкие к ним. Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспекти­ве, поэтому задачу грамотного изображения квадрата современная методика рисования предлагает решать с помощью эллипса, вокруг которого описывается квадрат.

💥 Видео

КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Построение квадрата циркулем по заданной сторонеСкачать