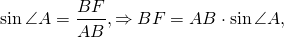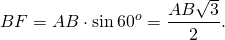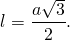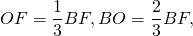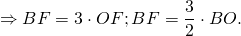Ак биссектриса равностороннего треугольника

В данной публикации мы рассмотрим основные свойства биссектрисы равностороннего треугольника, а также разберем пример решения задачи по данной теме.

Примечание: напомним, что равносторонним называется треугольник, в котором равны как все стороны, так и все углы.

Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Свойства биссектрисы равностороннего треугольника

Свойство 1

Любая биссектриса равностороннего треугольника одновременно является и медианой, и высотой, и серединным перпендикуляром.

BD – биссектриса угла ABC, которая также является:

• высотой, опущенной на сторону AC;
• медианой, делящей сторону AC на два равных отрезка (AD = DC);

Свойство 2

Все три биссектрисы равностороннего треугольника равны между собой.

Свойство 3

Биссектрисы равностороннего треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.

Свойство 4

Точка пересечения биссектрис равностороннего треугольника является центром описанной и вписанной окружностей.

• r – радиус вписанной окружности;
• R – радиус описанной окружности;
• R = 2r.

Свойство 5

Биссектриса равностороннего треугольника делит его на два равновеликих (равных по площади) прямоугольных треугольника.

Примечание: Три биссектрисы равностороннего треугольника делят его на 6 равновеликих прямоугольных треугольников.

Свойство 6

Любая из внешних биссектрис угла равностороннего треугольника параллельна стороне, лежащей напротив данного угла.

• AD и AE – внешние биссектрисы, параллельные BC;
• BK и BL – внешние биссектрисы, параллельные AC;
• CM и CN – внешние биссектрисы, параллельные AB.

Свойство 7

Длину биссектрисы ( l_a ) равностороннего треугольника можно выразить через его сторону.

где a – сторона треугольника.

Видео:Задание 9 ОГЭ от ФИПИСкачать

Пример задачи

Радиус вписанной в равносторонний треугольник окружности равен 4 см. Найдите длину его стороны.

Решение

Согласно Свойствам 3 и 4, рассмотренным выше, радиус вписанной окружности составляет 1/3 часть от биссектрисы равностороннего треугольника. Следовательно, вся ее длина равняется 12 см (4 см ⋅ 3).

Теперь мы можем найти сторону треугольника с помощью формулы ниже (получена из Свойства 7):

Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Биссектриса равностороннего треугольника

Какими свойствами обладает биссектриса равностороннего треугольника? Как, зная сторону правильного треугольника, найти его биссектрису? Чему равна длина биссектрисы через радиус вписанной и описанной окружностей?

(свойство биссектрисы равностороннего треугольника)

В равностороннем треугольнике биссектриса, проведённая к любой стороне, является также его медианой и высотой.

Пусть в треугольнике ABC AB=BC=AC.

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.

Проведем биссектрису BF.

По свойству равнобедренного треугольника, BF является также его медианой и высотой.

Аналогично, треугольник ABC — равнобедренный с основанием BC, треугольник ABC — равнобедренный с основанием AB, а его биссектрисы AK и CD — еще и медианы и высоты.

Что и требовалось доказать .

(свойство биссектрис равностороннего треугольника)

Все три биссектрисы равностороннего треугольника равны между собой.

Пусть в треугольнике ABC AB=BC=AC.

AK, BF CD — биссектрисы треугольника ABC.

В треугольниках ABF, BCD и CAK:

• AB=BC=CA (по условию)
• ∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника)
• ∠ABF=∠BCD=∠CAK (как как AK, BF CD — биссектрисы равных углов).

Значит, треугольники ABF, BCD и CAK равны (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон: AK=BF=CD.

Что и требовалось доказать .

Из теорем 1 и 2 следует, что в равностороннем треугольнике все биссектрисы, медианы и высоты равны между собой.

1) Найдём биссектрису равностороннего треугольника через его сторону.

В треугольнике ABC AB=BC=AC=a.

BF — биссектриса, BF=l.

По свойствам равностороннего треугольника, BF — высота ∆ ABC, ∠A=60º.

Из прямоугольного треугольника ABF по определению синуса

Таким образом, формула биссектрисы равностороннего треугольника по его стороне:

2) Найдём биссектрису равностороннего треугольника через радиусы вписанной и описанной окружностей.

В правильном треугольнике ABC центры вписанной и описанной окружностей совпадают.

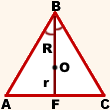
Центр вписанной окружности — точка пересечения биссектрис треугольника. Биссектрисы равностороннего треугольника также являются его медианами. Медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины.

Следовательно, точка O — центр вписанной и описанной окружностей, OF — радиус вписанной окружности, OF=r, BO — радиус описанной окружности, BO=R и BO:OF=2:1.

Таким образом, длина биссектрисы через радиус вписанной окружности равна

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

2) АК — биссектриса равностороннего треугольника АВС?

Геометрия | 5 — 9 классы

2) АК — биссектриса равностороннего треугольника АВС.

Докажите, что прямая ВС касается окружности с центром в точке А и радиусом АК.

Биссектриса любого угла равностороннего треугольника является и медианой, и, что важно для данного случая, — высотой, т.

Радиус АК перпендикулярен ВС, как мы только что выяснили, поэтому ВС касается окружности в точке К.

Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

В треугольник АВС с прямым углом С вписана окружность с центром О, касающаяся сторон треугольника АВ, ВС, АС в точках М , Т , Р соответственно?

В треугольник АВС с прямым углом С вписана окружность с центром О, касающаяся сторон треугольника АВ, ВС, АС в точках М , Т , Р соответственно.

Расстояние от точки пересечения биссектрис треугольника АВС до вершины С равно корню из 8 см.

Найдите радиус окружности, угол ТОР и угол ТМР.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

В окружность с центром в О вписан треугольник АВС?

В окружность с центром в О вписан треугольник АВС.

Окружность, которая проходит через точки А, В и О, касается прямой АС в точке А.

Известно, что угол АСВ = 40° Найти угол АВС.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Ребята, помогите?

Две окружности радиусов 4 и 8 касаются в точке А.

Через точку А проведена прямая, пересекающая большую окружность в точке В, а меньшую – в точке С.

Найдите АВ, если известно, что ВС = 6 корень из 2.

Точка Р лежит на дуге окружности, описанной около равностороннего треугольника АВС.

Докажите, что РС = РА + РВ.

Видео:Формулы равностороннего треугольника #shortsСкачать

Из точки A проведены две прямые, касающиеся окружности радиуса R в точках C и B, причём треугольник ABC — равносторонний?

Из точки A проведены две прямые, касающиеся окружности радиуса R в точках C и B, причём треугольник ABC — равносторонний.

Найдите его площадь.

Видео:Найдите биссектрису прямоугольного треугольника с катетами 3 и 5 ★ Как решать?Скачать

Точка D — середина основания АВ равнобедренного треугольника АВС ?

Точка D — середина основания АВ равнобедренного треугольника АВС .

Докожите что прямая АВ касается окружности с центром в точке С и радиусом CD срочно!

Только понятно для восьмого класса.

Видео:ОГЭ 16🔴Скачать

Основание АС равнобедренного треугольника АВС равно 10?

Основание АС равнобедренного треугольника АВС равно 10.

Окружность радиусом 7, 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается АС в его середине.

Найти радиус окружности, вписанной в треугольник АВС.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Докажите, что стороны равностороннего треугольника касаются окружностей, проведенных с центрами в его вершинах и радиусами, равными любой из его биссектрис ?

Докажите, что стороны равностороннего треугольника касаются окружностей, проведенных с центрами в его вершинах и радиусами, равными любой из его биссектрис !

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

А) Отрезок АВ гипотенуза прямоугольного треугольника АВС?

А) Отрезок АВ гипотенуза прямоугольного треугольника АВС.

Докажите что прямая ВС является касательной к окружности с центром А радиуса АС, а прямая АВ не является касательной к окружности с центром С радиуса ВС.

(Рисунок чертежа внизу кто не знает как нарисовать) б)В прямоугольном треугольнике АВС гипотенуза Ав равна 20 см и угол А = 60 градусов.

Каким должен быть радиус окружности с центром А чтобы она : а) касалось прямой ВС б) не имела с прямой ВС общих точек в) имела с прямой ВС две общие точки?

В)В прямоугольном треугольнике АВС катеты АС и ВС равны и АВ = 10 см.

Каково ваимное расположение АВ и окружности с центром С радиусом 5см.

Видео:3 свойства биссектрисы #shortsСкачать

25 баллов геометрия?

25 баллов геометрия.

Точка D — середина основания АВ равнобедренного треугольника АВС .

Докожите что прямая АВ касается окружности с центром в точке С и радиусом CD.

Видео:Построение биссектрисы в треугольникеСкачать

Окружность, вписанная в треугольник АВС, касается сторон ВС в точке D?

Окружность, вписанная в треугольник АВС, касается сторон ВС в точке D.

Докажите, что если луч AD — биссектриса угла треугольника, то АВ = АС.

Перед вами страница с вопросом 2) АК — биссектриса равностороннего треугольника АВС?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Сумма внутреннего и внешнего углов равна 180° Находим внутренний угол при вершине b (т. Е. ∠abc) : 180 — 140 = 40° Поскольку треугольник abc — равнобедренный, следовательно углы при основании равны, следовательно∠abc = ∠acb = 40°.

Tgα = ВД(высоты) / 0, 5 * АС⇒10 / 7 = ВД / 14 ВД(высота) = 10 * 14 / 7 = 20⇒Sавс = 1 / 2 * 28 * 20 = 280.

1) 6 : 2 = 3 см — середина АВ и середина СD , так как они равны. 6 см + 3 см + 3 см = 12 см Ответ : 12 см 2) Не знаю как решать , извини. 3) Возьмем АВ за х AM = MB = x 2 Тогда MN = BN = MB 2 = x 4 AM : MN = x 2 : x 4 = 2 : 1 BN : AM = x ..

SΔ = (a * ha) / 2 SΔ = (14 * 6) / 2 = 42 см².

По твоему чертежу, но без окружности : А 0 — центр окружности I А0 — радиус I 0В — радиус I 0С — радиус I0___________C ∠А0С = ∠В0С = 90° I Соедини· А и· С I Получим равнобедренныйΔ А0С I А0 = 0С (это радиусы) I В равнобедренномΔ углы при основании B ..

1)х + х + 160 = 180 2х = 20 х = 10 2)160 + 10 = 170.

Так как треугольник авс равнобедренный ав = вс то и ам = ск тогда треугольник вмк равнобедренный.

Дано : угол АВ, угол АD = 80градусов, угол ВD, угол AC = углуCB (это равенствопоказывает то, что С — биссектриса АВ), уголAD = углуDC. Найти : уголBD Решение : 1) уголAD× 2 = углуAC уголAC = углуCB 80× 2 = 160 — угол CB 2) уголDC + уголCB = углуBD 8..

АС = 50 + 16 = 66 М = АВ / 2 = 50 / 2 = 25 см К = ВС / 2 = 16 / 2 = 8 МК = 66 — 33 = 33 см.

1) а не параллельно b, т. К. угол4 = 180 — 60 = 120градусов (т. К. угол3 и угол4 смежные)угол4 и угол 1 являются накрест лежащими, но они не равны, значит а не параллельна b. 2) угол3 + угол4 = 180градусов, т. К. они односторонние. Пусть угол3 =..

🎥 Видео

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

№272. В равностороннем треугольнике ABC проведена биссектриса AD. Расстояние от точки DСкачать

Построение биссектрисы угла. 7 класс.Скачать

ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Геометрия Равносторонний треугольникСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать