Квадрат описанный вокруг окружности рисунок

Квадрат – ромб, у которого все углы прямые.

Квадрат – прямоугольник с равными сторонами.

Квадрат – параллелограмм, у которого все стороны равны и все углы равны.

Видео:ОГЭ Площадь квадрата, описанного около окружности #огэ #огэ2023 #алгебра #огэматематикаСкачать

Свойства квадрата

Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.

Видео:Найти площадь квадрата описанного около окружности радиуса 19Скачать

Признаки квадрата

Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.

2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.

Видео:Найдите площадь квадрата, описанного вокруг ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Описанная окружность

Около квадрата можно описать окружность. Сторона и радиус окружности связаны соотношением:

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Вписанная окружность

В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением:

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Площадь квадрата

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:2026 Найдите площадь квадрата описанного около окружности радиуса 14Скачать

РИСУНОК КВАДРАТА, ОПИСАННОГО ВОКРУГ ОКРУЖНОСТИ В ПЕРСПЕКТИВЕ

ЦЕЛЬ ЗАДАНИЯ. Научиться рисовать правильный квадрат в перспективе, описывая его вокруг окружности.

ПОСТАНОВКА ЗАДАНИЯ. Изобразите несколько горизонтальных и вертикальных окружностей в перспективе (эллипсов), опишите вокруг эллипсов квадраты в угловой и фронтальной перспективах.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Горизонтальная окружность. Нарисуйте окружность, лежащую на горизонтальной плоскости. Вы уже знаете, что на перспективном рисунке такая окружность изображается как эллипс, оси которого – горизонтальная и вертикальная прямые.

В угловой перспективе стороны горизонтального квадрата имеют две точки схода. Сначала задайте одно из направлений, соответствующее любым двум параллельным сторонам квадрата, а затем найдите второе, ему перпендикулярное. Для этого проведите прямую произвольного направления (среднюю линию квадрата) через центр окружности (рис. 2.18). Полученные на пересечении этой прямой с эллипсом точки 1 и 3 являются точками касания сторон квадрата к окружности. Проведите касательные через эти точки. Обратите внимание, что на рисунке полученные прямые (две стороны квадрата) сходятся в перспективе. Теперь проведите вторую среднюю линию квадрата, параллельную уже нарисованным сторонам (рис. 2.19). Она пройдет через центр окружности и даст нам на пересечении с эллипсом еще пару точек – 2 и 4. Эти точки также являются точками касания сторон квадрата к окружности. Проведите прямые, касательные к эллипсу в этих точках. Эти касательные параллельны прямой 7 – 3, т. е. уходят вместе с ней в одну точку схода на горизонте (рис. 2.20). Внимательно проверьте рисунок. В полученном квадрате прямые 1 – 3 и 2 – 4 параллельны соответствующим сторонам квадрата, а точки 1, 2, 3, 4 делят его стороны пополам. Проведите диагонали квадрата – они должны пересекаться в центре окружности.

Во фронтальной перспективе квадрат имеет две горизонтальные стороны и две стороны, сходящиеся в точке схода на линии горизонта. Построение такого квадрата ведется по той же схеме, что и построение квадрата в угловой перспективе. Средняя линия 1 – 3 совпадает с малой осью эллипса. Изобразите горизонтальные стороны квадрата как касательные к эллипсу в точках 1 и 3 (рис. 2.21). Проведите горизонтальную среднюю линию через центр окружности (рис. 2.22). Касательные к эллипсу в точках 2 и 4 определяют положение двух других сторон квадрата. Полученная таким образом фигура, ограниченная четырьмя касательными и есть описанный вокруг эллипса квадрат (рис. 2.23). Проверьте правильность построения квадрата при помощи диагоналей.

Вертикальный квадрат. Последовательность построения вертикального квадрата, описанного вокруг окружности, рассмотрим на примере, когда перед рисующим ставится задача описать вокруг горизонтального цилиндра четырехгранную призму, лежащую на горизонтальной плоскости. При таком положении цилиндра окружности его оснований будут вертикальными.

Начните построение с ближнего к вам основания. Описанный вокруг него квадрат имеет две вертикальные стороны, которые остаются вертикальными и на перспективном рисунке. Проведите две вертикальные касательные к эллипсу и найдите точки 2 и 4. Прямая, соединяющая их, будет иметь горизонтальное направление (рис. 2.24). Теперь проведите вертикальную прямую через центр окружности (точку, смещенную относительно центра эллипса дальше от зрителя) и найдите точки 1 и

3 (рис. 2.25). Прямые, касательные к эллипсу в этих точках, параллельны прямой 4 – 2, уходят с ней в одну точку схода на горизонте и определяют положение двух горизонтальных сторон квадрата (рис. 2.26). Второе основание призмы можно получить путем аналогичных построений. Соединив соответствующие вершины ближнего и дальнего оснований, завершите рисунок призмы, описанной вокруг цилиндра (рис. 2.27). Проверить правильность рисунка можно, проследив параллельность длинных сторон боковых граней призмы: они должны уходить в одну точку схода с осью цилиндра и его образующими.

Для закрепления этого материала подобные построения рекомендуется проделать несколько раз. Свободное владение этими навыками позволит вам перейти к перспективному изображению куба и других геометрических тел.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:Задание 3 ЕГЭ по математике. Урок 47Скачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:Построение правильного квадрата.Скачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:ОГЭ 17 заданиеСкачать

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:Геометрия Во сколько раз площадь квадрата, описанного около окружности больше площади квадратаСкачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Видео:Построить описанную окружность (Задача 1)Скачать

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Видео:Как построить квадрат, два способаСкачать

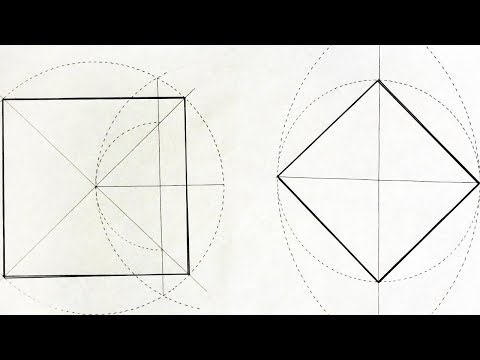
Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Видео:Найдите площадь квадрата, описанного около окружности радиуса 4.Скачать

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

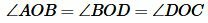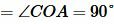(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

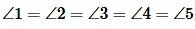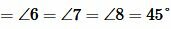(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

📺 Видео

Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать