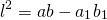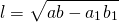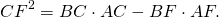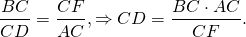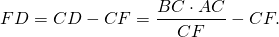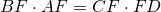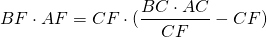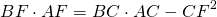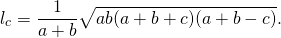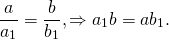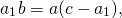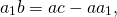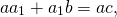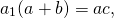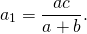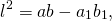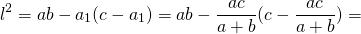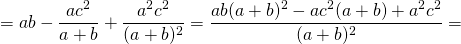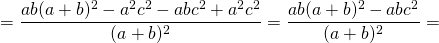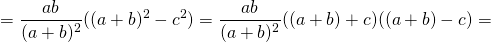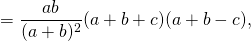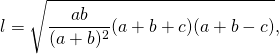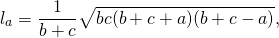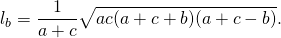Квадрат биссектрисы в треугольнике равен (2 видео)

Длина биссектрисы треугольника

Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.

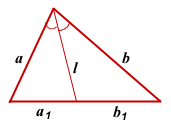
I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.

Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Дано:

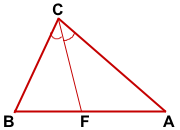
СF — биссектриса ∠ABC

Доказательство:

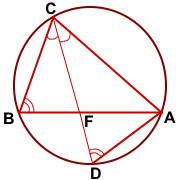
Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.

Рассмотрим треугольники BCF и DCA.

∠BCF=∠DCA (по условию);

Значит, треугольники BFC и DCA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Что и требовалось доказать.

II. Через три стороны треугольника

Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле

По свойству биссектрисы треугольника:

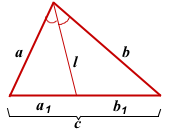
Согласно утверждению 1,

Что и требовалось доказать.

III Через две стороны треугольника и угол между ними.

Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле

Видео:Формула для биссектрисы треугольникаСкачать

Все формулы биссектрисы в треугольнике

L — биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b — стороны треугольника

с — сторона на которую опущена биссектриса

d, e — отрезки полученные делением биссектрисы

γ — угол ABC , разделенный биссектрисой пополам

p — полупериметр, p =(a+b+ c )/2

Длина биссектрисы через две стороны и угол, ( L ):

Длина биссектрисы через полупериметр и стороны, ( L ):

Длина биссектрисы через три стороны, ( L ):

Длина биссектрисы через стороны и отрезки d , e , ( L ):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Докажите, что квадрат биссектрисы треугольника равен произведению сторон, её заключающих, без произведения отрезков третьей стороны, на которые она разделена биссектрисой.

Пусть M — точка пересечения продолжения биссектрисы CD треугольника ABC с описанной около этого треугольника окружностью. Тогда треугольник CBD подобен треугольнику CMA по двум углам. Поэтому

= , или CD(CD + DM) = AC . BC,