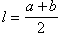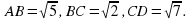Квадрат abcd вписан в окружность хорда

БАЗА ЗАДАНИЙ

Задание № 16. Планиметрия с доказательством.

1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.

2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3

3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2.
Ответ: б) 18√3

4. В треугольнике ABC точки A ₁ , B ₁ , C ₁ — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A₁, B₁, C₁, H— лежат на одной окружности.
б) Найдите A₁ H, если BC = 2√3.

5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10

6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4

7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6

8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.

9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.

10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.

11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88

12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC = 55°.

13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.

14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C ₁ , B ₁ соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB ₁ C ₁ .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B ₁ C ₁ =6 и площадь треугольника AB ₁ C ₁ в восемь раз меньше площади четырёхугольника BCB ₁ C _{1 .}

15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.

16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.

17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65

18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4

19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC = (KL+KM-LM)/2 .

б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2

20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3

21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1

22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36

23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4

24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.

25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.

26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.

27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.

28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Задача 16 (С4). Планиметрия. Комбинация окружности и четырехугольника.

Продолжим разговор о различных свойствах окружности, рассмотрим задачи на комбинации окружности и четырехугольника.

Конспект занятия «Задача 16 (С4). Планиметрия. Комбинация окружности и четырехугольника.»

Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

Две несмежные стороны четырехугольника называются противоположными. Две вершины, не являющиеся соседними, называются также противоположными.

Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма

противолежащие стороны равны;

противоположные углы равны;

диагонали точкой пересечения делятся пополам;

сумма углов, прилежащих к одной стороне, равна 180°;

сумма квадратов диагоналей равна сумме квадратов всех сторон:

Четырехугольник является параллелограммом, если:

Две его противоположные стороны равны и параллельны.

Противоположные стороны попарно равны.

Противоположные углы попарно равны.

Диагонали точкой пересечения делятся пополам.

Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны.

Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией.

Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

ее средняя линия параллельна основаниям и равна их полусумме;

если трапеция равнобокая, то ее диагонали равны и углы при основании равны;

если трапеция равнобокая, то около нее можно описать окружность;

если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.

Четырехугольник является трапецией, если его параллельные стороны не равны

Прямоугольником называется параллелограмм, у которого все углы прямые.

Свойства прямоугольника

все свойства параллелограмма;

Параллелограмм является прямоугольником, если:

Один из его углов прямой.

Его диагонали равны.

Ромбом называется параллелограмм, у которого все стороны равны.

Свойства ромба

Все свойства параллелограмма;

диагонали являются биссектрисами его углов.

Параллелограмм является ромбом, если:

Две его смежные стороны равны.

Его диагонали перпендикулярны.

Одна из диагоналей является биссектрисой его угла.

Квадратом называется прямоугольник, у которого все стороны равны.

Свойства квадрата

все углы квадрата прямые;

диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.

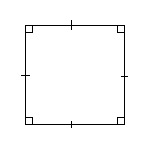
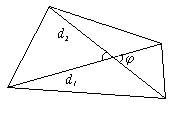
Произвольный выпуклый четырехугольник
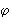
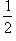
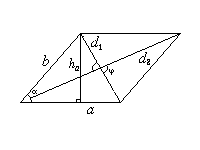
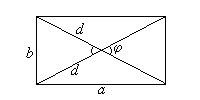
d₁, d₂ — диагонали; — угол между ними; S — площадь.

S =d₁d₂ sin

Параллелограмм
a и b — смежные стороны; 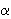— угол между ними; h_a — высота, проведенная к стороне a.

S = ab sin

S =d₁d₂ sin

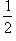
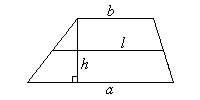
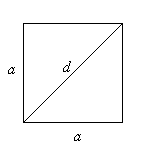
Трапеция
a и b — основания; h — расстояние между ними; l — средняя линия.

Прямоугольник

S =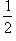d₁d₂ sin

Ромб

S = a 2 sin

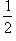
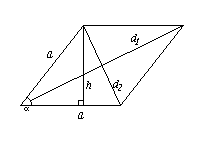
S =d₁d₂

Квадрат
d — диагональ.

S =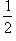d 2

Определить острый угол ромба, в котором сторона есть среднее геометрическое его диагоналей.

На сторонах квадрата ABCD отмечены точки M , N и K , где M – середина AB , N лежит на стороне BC , причем 2 BN = NC , K лежит на стороне DA , причем 2 DK = KA . Найти синус угла между прямыми MC и NK .

В па­рал­ле­ло­грам­ме ABCD бис­сек­три­сы углов при сто­ро­не AD делят сто­ро­ну BC точ­ка­ми M и N так, что BM : MN = 1 : 2. Най­ди­те BC если AB = 12.

В па­рал­ле­ло­грамм впи­са­на окруж­ность.

а) До­ка­жи­те, что этот па­рал­ле­ло­грамм — ромб.

б) Окруж­ность, ка­са­ю­ща­я­ся сто­ро­ны ромба, делит её на от­рез­ки, рав­ные 3 и 2. Най­ди­те пло­щадь четырёхуголь­ни­ка с вер­ши­на­ми в точ­ках ка­са­ния окруж­но­сти со сто­ро­на­ми ромба.

Сто­ро­на CD пря­мо­уголь­ни­ка ABCD ка­са­ет­ся не­ко­то­рой окруж­но­сти в точке M. Про­дол­же­ние сто­ро­ны AD пе­ре­се­ка­ет окруж­ность в точ­ках P и Q, причём точка P лежит между точ­ка­ми D и Q. Пря­мая BC ка­са­ет­ся окруж­но­сти, а точка Q лежит на пря­мой BM.

б) Из­вест­но, что CM = 17 и CD = 32. Най­ди­те сто­ро­ну AD.

Квад­рат ABCD впи­сан в окруж­ность. Хорда CE пе­ре­се­ка­ет его диа­го­наль BD в точке K.

а) До­ка­жи­те, что

б) Най­ди­те от­но­ше­ние CK и KE, если .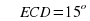

Четырехугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке P .

а) Докажите, что AD * BP = BC * DP .

б) Найдите площадь треугольника APC , если известно, что BD =2 AC , а площадь четырехугольника ABCD равна 36.

Высота равнобедренной трапеции ABCD (В C и AD — основания) равна длине ее средней линии.

а) докажите, что диагонали трапеции перпендикулярны.

б) Найдите радиус окружности, касающейся сторон AB , BC и CD трапеции, если известно, что BC =4, AD =6.

Четырехугольник ABCD со взаимно перпендикулярными диагоналями AC и BD вписан в окружность.

а) Докажите, что квадрат диаметра окружности равен сумме квадратов противоположных сторон четырехугольника.

б) Найдите площадь четырехугольника ABCD , если известно что

Видео:Математика 11, задача по геометрии, 2-я часть ЕГЭ, задача 16Скачать

Задания по теме для самостоятельного решения

Задание 1

Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Задание 2

Бис­сек­три­са угла ADC па­рал­ле­ло­грам­ма ABCD пе­ре­се­ка­ет пря­мую AB в точке E. В тре­уголь­ник ADE впи­са­на окруж­ность, ка­са­ю­ща­я­ся сто­ро­ны AE в точке K и сто­ро­ны AD в точке T. Най­ди­те угол BAD, если из­вест­но, что AD = 6 и KT = 3. Ответ запишите числом в градусах без пробелов и знаков препинания.

Задание 3

В четырёхугольнике ABCD известно, что ABD = ACD = 45 o , BAC = 30 o , BC = 1. Найдите AD. В ответ запишите квадрат искомой величины.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В квадрат ABCD, длина стороны которого равна а, вписана окружность. Окружность касается стороны CD в точке Е. Найдите длину хорды, соединяющей точки, в которых

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Ваш ответ

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

решение вопроса

Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,921
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

🎬 Видео

ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать

Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

ЕГЭ-2016. Математика. Задание 16 (планиметрия)Скачать

Задание 26 Вписанный квадратСкачать

ЕГЭ. Задачи на окружность. ХордаСкачать

ОГЭ по математике. Задание 16Скачать

ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружность, диаметр, хорда геометрия 7 классСкачать

Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Сможешь найти длину хорды? Окружность, вписанная в квадратСкачать

Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать