Куб с окружностями рисунок

Здравствуйте, подписчики моего блога!

Многие сталкивались со сложностью в рисовании, когда хотели изобразить сложный по форме объект. Дело в том, что в основе всех сложных структур скрываются простые формы. И куб – одна из таких форм. Сегодня мы подробно разберем, как построить куб.

Видео:Изображение в изометрической проекции окружностей, вписанных в кубСкачать

Перспектива

Куб – это геометрическое тело, состоящее из 6 плоскостей. Знаете, чем отличается куб от квадрата? Куб – это объемная фигура. А при рисовании любых объемных фигур нужно помнить о перспективе.

Из-за законов перспективы стороны куба будут сокращаться, иными словами становиться меньше.

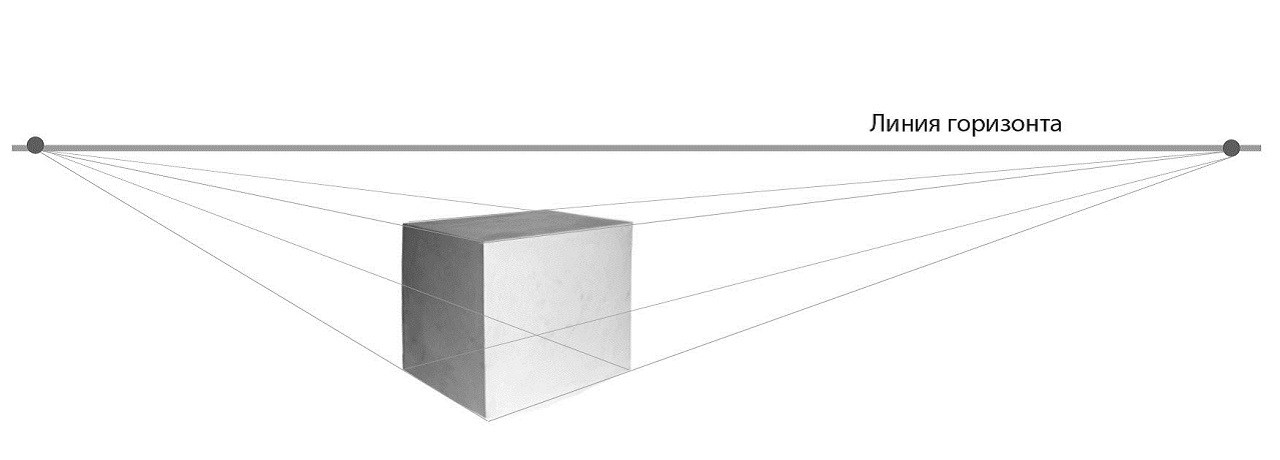
Для начала нужно определить линию горизонта. Это необходимо для того, чтобы правильно построить куб в перспективе.

Линия горизонта – это уровень глаз художника. На ней будут располагаться две точки схода. В каждую из этих точек придёт по 4 линии. Наглядно такой рисунок будет выглядеть следующим образом:

Видео:Изображение окружности в перспективе. Эллипс.Скачать

Рисуем пошагово

Чтобы было проще воспринять последовательность действий, давайте нарисуем куб пошагово.

Прежде чем заниматься перспективой куба, нужно наметить верные размеры предмета и определить его положение в листе. Куб не должен быть слишком маленьким или, наоборот, слишком большим.

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

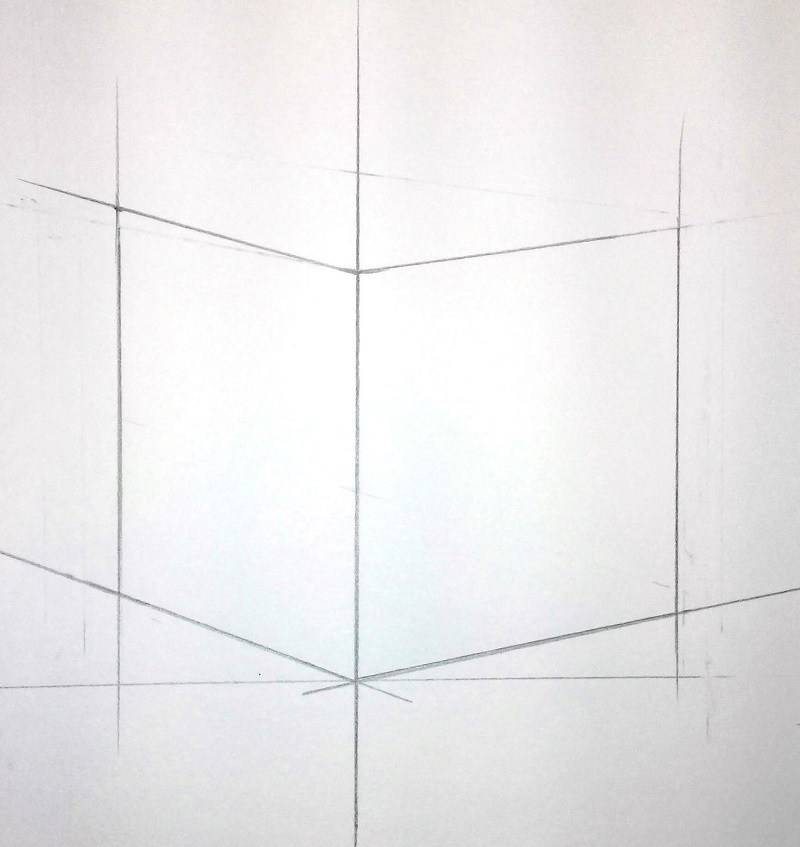
Шаг 1 — Композиция

Композиция – это начало любой работы. От точного нахождения композиции зависит 50% успеха работы.

Следует оставить чуть больше расстояния сверху, чем снизу. Это придаст ощущение весомости.

Начинаем рисунок с самого ближнего к нам ребра куба. Наметьте его так, чтобы оно не совпадало с центром листа. Легкими засечками определяем высоту этого ребра. Так как оно находится ближе всего, его высота будет больше остальных ребер.

Видео:УРОК 1.КАК НАРИСОВАТЬ КУБ.Академический рисунок.Перспектива.Рисунок карандашом.Скачать

Шаг 2 — Сокращение

Плоскости в кубе заметно удаляются в силу перспективного сокращения. Чтобы верно определить это сокращение на листе, необходимо определить углы наклона ребер.

Проводим горизонтальную линию, параллельную листу бумаги, она поможет определить какой угол меньше, а какой больше. Тренируйте свой глаз, переводите взгляд с куба на рисунок, таким образом, перепроверяя себя.

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

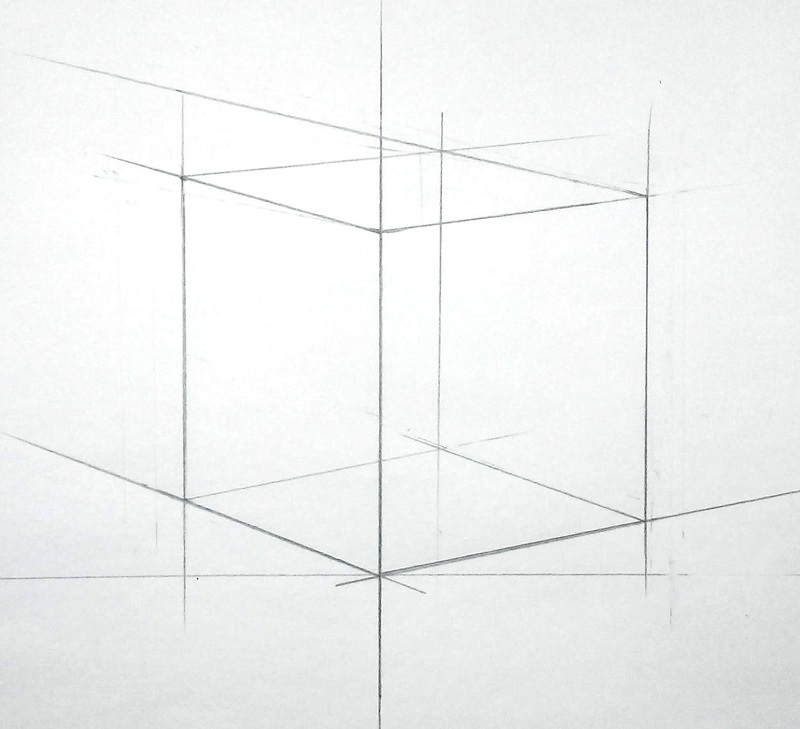
Шаг — 3 — Линейная перспектива

Чтобы куб «лег» в пространство, ребра, удаленные от нас, мы рисуем выше и меньше. Этот прием лежит в основе линейной перспективы. Найдите, где заканчиваются эти ребра и обозначьте их точками. Сечение куба по трем точкам – это верных способ при построении.

Соединяем горизонтальными линиями пересечения плоскостей в кубе. Помните о том, что они сокращаются, и, если, мы их продлим, то они сойдутся в точке схода.

Невидимые грани мы также должны нарисовать. При правильном построении нужно проверить все сокращения, чтобы не было обратной перспективы.

Видео:КАК РИСОВАТЬ ЭЛЛИПСЫ. Простой и быстрый способ рисования ЭЛЛИПСОВСкачать

Шаг 4 — Проверка пропорций

Также можно использовать метод визирования. Вы наверняка замечали, как художники вытягивают руку и измеряют пропорции? Это и есть метод визирования.

Для того, чтобы проверить пропорции, закройте один глаз, возьмите карандаш и на вытянутой руке сопоставьте его кончик с верхом переднего ребра куба. Большой палец передвиньте в то место, где ребро заканчивается.

Высота ребра найдена. Теперь, не переставляя палец, наклоните кисть руки на 90 градусов и уже по горизонтали сопоставьте величину одного ребра с другим. Таким образом вы можете проверять и другие величины.

С опытом художники измеряют пропорции «на глаз», это значит, что они обходятся без метода визирования. Их глаз настолько натренирован, что видит размеры без измерений.

Итак, линейное построение подошло к концу, а значит, мы переходим к воздушной перспективе или, проще говоря, к штрихованию.

Видео:мини-урок "зарисовка куба"Скачать

Штрихование

Основная задача рисунка – это передать объем. Внимательно посмотрите на предмет, определите для себя тональность каждой из сторон.

Штриховать следует по форме куба. Внимательно подходите к штриховке, не стоит излишне чернить, все-таки мы рисуем гипсовый куб.

Набирайте тон постепенно, не старайтесь все сделать за один подход. Штрихи можно накладывать и в диагональном направлении.

Используйте карандаши разной мягкости. Для освещённой стороны отлично подойдет твердый карандаш – H, для полутона – HB, а для теневой стороны – B.

В некоторых случаях карандаши стоит выбирать индивидуально: некоторые люди имеют «легкую» руки и штрихуют еле заметно, а есть те, кто с помощью HB может довести рисунок до черноты.

Видео:Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

Падающая тень

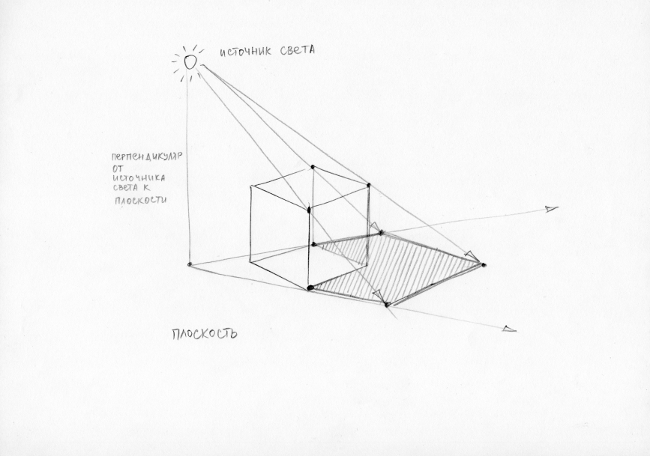
Как построить тень от куба? Чтобы падающая тень была убедительной, давайте рассмотрим основные принципы построения тени на поверхности листа.

1. Определяем местонахождения источника света.
2. Проводим перпендикуляр от источника света к плоскости, где находится наш предмет.
3. От точки, где перпендикуляр пересекается с плоскостью, проводим линии в касание с углами куба.
4. Проецируем воображаемые лучи от источника света, которые проходят по вершинам 5 куба. Намечаем точки соприкосновения лучей и плоскости.
5. Соединяем найденные точки на плоскости и получаем конфигурацию тени.

Падающая тень всегда темнее, чем собственная тень на предмете. Чем ближе она подходит к объекту, тем темнее она становится.

На самом кубе тон становится также активнее на границе двух плоскостей – освещенной и теневой. Теневая сторона, по мере удаления в пространство, высветляется за счет отраженного света от поверхности. Рефлексы помогают передать световоздушное пространство.

Видео:Откройте секреты академического рисунка и нарисуйте куб / видео уроки рисованияСкачать

Заключение

Мы поговорили о сечении куба плоскостью, о том, как правильно построить куб с натуры в перспективе. Рисование простых геометрических тел весьма полезно для начинающих и тех, кто хочет овладеть академическим рисунком.

Геометрия и расположение плоскостей в пространстве очень хорошо тренирует зрительное восприятие.

Если у вас нет гипсового куба, не беда, смастерите куб из бумаги. Для первых упражнений главное – это понять основные принципы при построении. А затем, можно будет перейти к гипсовым фигурам.

Удачи в творчестве! Рисуйте то, что любите!

Если вам понравилась статья, поделитесь ей с друзьями!

Видео:Рисунок куба через эллипс. Полное видео построения куба от начала до конца.Скачать

Изображение окружностей в изометрической проекции

Рассмотрим, как в изометрической проекции изображаются окружности. Для этого изобразим куб с вписанными в его грани окружностями (рис. 3.16). Окружности, расположенные соответственно в плоскостях, перпендикулярных осям х, у, z, изображаются в изометрии в виде трех одинаковых эллипсов.

Рис. 3.16. Изометрические проекции окружностей, вписанных в грани куба

Для упрощения работы эллипсы заменяют овалами, очерчиваемыми дугами окружностей, их строят так (рис. 3.17). Вычерчивают ромб, в который должен вписываться овал, изображающий данную окружность в изометрической проекции. Для этого на осях откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности (рис. 3.17, а). Через полученные точки a, b, с, d проводят прямые, образующие ромб. Его стороны равны диаметру изображаемой окружности.

Рис. 3.17. Построение овала

Из вершин тупых углов (точек А и В) описывают между точками а и b, а также с и d дуги радиусом R, равным длине прямых Ва или Вb (рис. 3.17, б).

Точки С и Д лежащие на пересечении диагонали ромба с прямыми Ва и Вb, являются центрами малых дуг, сопрягающих большие.

Малые дуги описывают радиусом R, равным отрезку Са (Db).

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Построение изометрических проекций деталей

Рассмотрим построение изометрической проекции детали, два вида которой даны на рис. 3.18, а.

Построение выполняют в следующем порядке. Сначала вычерчивают исходную форму детали – угольник. Затем строят овалы, изображающие дугу (рис. 3.18, б) и окружности (рис. 3.18, в).

Рис. 3.18. Последовательность построения изометрической проекции детали

Для этого на вертикально расположенной плоскости находят точку О, через которую проводят изометрические оси х и z. Таким построением получают ромб, в который вписана половина овала (рис. 3.18, б). Овалы на параллельно расположенных плоскостях строят перенесением центров дуг на отрезок, равный расстоянию между данными плоскостями. Двойными кружочками на рис. 3.18 показаны центры этих дуг.

На тех же осях х и z строят ромб со стороной, равной диаметру окружности d. В ромб вписывают овал (рис. 3.18, в).

Находят центр окружности на горизонтально расположенной грани, проводят изометрические оси, строят ромб, в который вписывают овал (рис. 3.18, г).

Видео:Академический рисунок кубаСкачать

Понятие о диметрической прямоугольной проекции

Расположение осей диметрической проекции и способ их построения приведены на рис. 3.19. Ось z проводят вертикально, ось х – под углом около 7° к горизонтали, а ось у образует с горизонталью угол приблизительно в 41° (рис. 3.19, а). Построить оси можно, пользуясь линейкой и циркулем. Для этого из точки О откладывают по горизонтали вправо и влево по восемь равных делений (рис. 3.19, б). Из крайних точек восставляют перпендикуляры. Высота их равна: для перпендикуляра к оси х – одному делению, для перпендикуляра к оси у – семи делениям. Крайние точки перпендикуляров соединяют с точкой О.

Рис. 3.19. Расположение осей диметрической проекции

При вычерчивании диметрической проекции, как и при построении фронтальной, размеры по оси у сокращают в 2 раза, а по осям х и z откладывают без сокращений.

На рис. 3.20 показана диметрическая проекция куба с вписанными в его грани окружностями. Как видно из этого рисунка, окружности в диметрической проекции изображаются эллипсами.

Рис. 3.20. Диметрические проекции окружностей, вписанных в грани куба

Видео:Как нарисовать куб в перспективе карандашом | Рисунок для начинающих поэтапноСкачать

Технический рисунок

Технический рисунок – это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз. Им пользуются в тех случаях, когда нужно быстро и наглядно показать на бумаге форму предмета. Обычно в этом возникает необходимость при конструировании, изобретательстве и рационализации, а также при обучении чтению чертежей, когда с помощью технического рисунка нужно пояснить форму детали, представленной на чертеже.

Выполняя технический рисунок, придерживаются правил построения аксонометрических проекций: под теми же углами располагают оси, так же сокращают размеры по осям, соблюдают форму эллипсов и последовательность построения.

Видео:2 2 3 построение изометрии окружностиСкачать

Основы линейной перспективы: как нарисовать куб с любого ракурса

Советуем приготовить планшет или лист бумаги и ручку, чтобы все сразу попробовать. Читать эту статью просто так не имеет смысла — тут все про практику.

Освоив кубы, вы сможете рисовать любые объекты: машин, людей, архитектуру. Тоже с любого ракурса, быстро и понятно. Например, вот так можно свести к кубам фигуру человека:

Известный художник Скотт Робертсон рисует технику, отталкиваясь от геометрических примитивов.

Дальше будет много примеров. Советуем попробовать нарисовать основные моменты, чтобы лучше понять, о чем речь. Получится своеобразный конспект.

Статья написана по материалам ресурса How to sketch.

Рисовать куб с любого ракурса — это рисовать его в перспективе. Представьте камеру — она заменит нам наблюдателя. На расстоянии от камеры стоит куб. Между камерой и кубом находится стекло.

Стекло здесь — так называемая картинная плоскость. Проведем от камеры сквозь стекло линию — получится то, что называется лучом зрения (ЛЗ). Луч зрения всегда перпендикулярен картинной плоскости. Эти обозначения понадобятся нам дальше.

Нам нужно знать, как линии нашего объекта расположены в пространстве относительно чего-либо. Положение камеры — наша путеводная звезда. Рисовать в перспективе — значит представлять изображение с определенной точки зрения. Не бывает изображения без зрителя.

Дальше мы будем рассматривать сцену с двух точек зрения: то, как ее видит камера, и то, как она расположена относительно объекта. Это нужно, чтобы проще ориентироваться в пространстве.

Куб состоит из шести квадратных плоскостей, соединенных вместе. Чтобы нарисовать куб, нам нужно знать, как правильно расположить в пространстве квадрат во всех без исключения случаях и с любого возможного ракурса.

Здесь мы добавим в наш словарь новое слово — нормальная линия или просто нормаль. Нормаль — это линия, перпендикулярная какой-либо поверхности. Если вы поставите карандаш вертикально на стол, он будет совпадать с направлением нормальной линии. Вы можете встретить этот термин в 3D, но в 2D его тоже используют.

Возьмем квадрат и расположим его перед камерой. Если нормаль перпендикулярна картинной плоскости и тем самым совпадает с лучом зрения, значит, мы видим поверхность без каких-либо искажений. В данном случае — обычный квадрат.

Если мы наклоним нашу фигуру в каком-либо направлении, то нормаль больше не будет смотреть прямо на картинную плоскость. Поверхность прямоугольника сожмётся в том направлении, куда смотрит нормаль. Этот принцип называется сжатие по нормали. Каждая плоскость всегда сжимается только по своей нормальной линии.

На приведенном примере боковые стороны прямоугольника сужаются кверху (с точки зрения камеры). Так получается потому, что это параллельные линии, которые уходят вдаль (относительно картинной плоскости). А вот линии, параллельные картинной плоскости, никогда не сходятся.

Параллельные линии, которые уходят вдаль, сходятся на линии горизонта. Эта истина так широко известна и непреложна, что авторы никогда не пересматривают ее обоснование. А мы пересмотрим — чтобы лучше понять, о чем речь.

Наша камера стоит строго вертикально, то есть ее нижняя плоскость параллельна плоскости земли. Представим себе не один, а несколько горизонтальных прямоугольников перед камерой. По мере того, как эти плоскости всё выше поднимаются над землёй, они всё сильнее сжимаются. В какой-то момент плоскость визуально сожмется в плоскую линию — это будет линия горизонта.

Находим линию горизонта.

Параллельные линии, расположенные на горизонтальных плоскостях (на любой из них) сходятся на линии горизонта. Точки, в которых они сходятся, называются точками схода (ТС).

Как видите, у каждого набора параллельных линий есть своя собственная точка схода. Для перспективы типично наличие центральной (ЦТС), левой (ЛТС) и правой (ПТС) точек схода.

Теперь попробуем разобраться в том, как прямоугольники изменяются по мере увеличения расстояния от зрителя.

Возьмем несколько прямоугольников и выстроим их в ряд. Все они имеют одинаковый размер и расположены впритык друг к другу. И хотя в действительности все они имеют одинаковый физический размер, каждый последующий прямоугольник в перспективе становится меньше. Благодаря этому явлению параллельные линии «сходятся на линии горизонта».

Благодаря изменению размера наш мозг воспринимает глубину. Но оно происходит не линейно: каждый прямоугольник сжимается по своей нормали, когда его наклоняют относительно зрителя. Плоскость сжимается тем сильнее, чем она ближе к линии горизонта.

Проведём три горизонтальные линии в перспективе аналогично прямоугольникам выше. Изменяем только одно требование: интервалы между ними должны быть одинаковыми. Что мы увидим? Отрезок B в два раза короче, чем A, но C в шесть раз короче, чем B.

Это важно понимать при рисовании не только механизмов, но и природных форм. Даже фигуры человека. Как и любой другой объект, тело существует в пространстве. Важно точно знать, где именно расположены ключевые точки тела. А для этого нужно освоить измерения в перспективе. Набравшись опыта, вы сможете делать обоснованные догадки, уже не рисуя вспомогательные конструкции.

Теперь нам нужно нарисовать эллипсы. Тут нам пригодятся те же знания, что мы получили, изучая квадратные плоскости: потому, что плоскость может быть любой формы, в том числе овальной или круглой. У плоского круга или овала тоже есть нормальная линия, и она точно так же перпендикулярна поверхности плоскости.

Нормальная линия плоского эллипса всегда совпадает по направлению с его малой осью.

Важно помнить, что у круга всегда одинаковый диаметр, в каком бы направлении мы его не провели. После сжатия круг превращается в овал, и у него появляется самый длинный (большая ось эллипса) и самый короткий (малая ось эллипса) диаметры.

Большая ось не меняет свою длину, как бы сильно мы ни наклоняли плоскость. Малая ось перпендикулярна большой, а ее направление совпадает с нормальной линией. Длина малой оси меняется сильнее всего, когда мы наклоняем плоскость по отношению к камере.

Эллипсы помогают определить направление нормальной линии поверхности, поэтому их удобно использовать, даже если на рисунке нет видимых круглых плоскостей. Они подсказывают, в каком направлении сжимать плоскость, когда она наклонена по отношению к зрителю.

Еще эллипс может пригодится, чтобы определить угол наклона плоскости относительно зрителя. Сильнее наклон, сильнее сжатие.

И, последний, самый важный пункт. Эллипс помогает найти пропорции идеального квадрата: круг, вписанный в квадрат, касается каждой из четырех сторон точно посередине.

Помимо пропорций квадрата, нам нужно убедиться, что у нашей фигуры есть четыре прямых угла (по 90 градусов). Для этого необходимо правильно построить хотя бы один угол — три остальных встанут на свои места.

Эллипс поможет найти правильный угол между двумя линиями на одной плоскости.

Исходное расположение объектов. Смотрите ниже, как мы превращаем круг в квадрат.

Определяем пропорции квадрата с заданного ракурса, используя эллипс.

Проведем нормальную линию (она здесь вертикальная, потому что плоскость горизонтальная). Её можно проводить в разных местах — в зависимости от того, как мы хотим развернуть к себе угол будущего квадрата.

Как далеко нормаль должна выходить за пределы эллипса до той точки, где она пересекается с касательными? Это зависит от угла наклона эллипса.

Чем ближе линия горизонта к эллипсу (с учётом его размера), тем сильнее перспективное искажение, и тем быстрее сходятся линии. Это также значит, что объект или находится близко к зрителю, или он большой. Изображение выглядит так, как будто снято через широкоугольный объектив.

Если линия горизонта находится далеко от эллипса, перспективное искажение будет слабым. Линии будут сходиться медленно, объект покажется маленьким или будет расположен далеко от зрителя. Это эффект длиннофокусного объектива.

Здесь видно, что вертикальная линия в обоих случаях выходит за пределы эллипса на одно и то же расстояние. Нижний угол квадрата одинаковый. Разница только в силе перспективы. И ещё раз напоминаем: линия горизонта перпендикулярна нормали эллипса (малой оси).

Горизонт — это по сути ещё одна плоскость, параллельная нашему эллипсу. Просто она полностью наклонена по отношению к зрителю.

Итак, наш эллипс готов.

У куба шесть граней, но одновременно мы можем увидеть лишь три из них. Так что, простоты ради, мы сосредоточимся только на видимых сторонах (пока). Начнем с верхней грани. Вы уже знаете, как изобразить горизонтальный квадрат в любом возможном положении, так что сделайте это — нарисуйте квадрат вокруг эллипса.

Теперь нужно дорисовать две боковые грани. Чтобы найти их, используйте вертикально расположенные рёбра куба — нормали к верхней плоскости.

Осталось еще узнать длину вертикального ребра. Оно параллельно картинной плоскости и становится длиннее, когда перемещается ближе к нам в пространстве (как и любой другой объект), в соответствии с конвергенцией (сближением) линий.

Есть одна хитрость, которая помогает проверить, правильно ли мы построили боковые грани. Это можно сделать с помощью эллипса. Нарисуйте эллипс, малая ось которого направлена в правую точку схода. Эллипс должен касаться рёбер куба посередине. Затем просто закройте снизу левую грань с помощью линии, идущей к левой точке схода. А потом правую грань — линией, идущей к правой точке схода:

Для этого вернемся к рисованию прямоугольников. У каждого прямоугольника есть диагонали, они пересекаются в его центре. Диагонали помогают нам рисовать одинаковые прямоугольники.

Давайте потренируемся. Найдите центр прямоугольника, используя диагонали.

Нарисуйте среднюю линию прямоугольника и продолжите ее в том направлении, куда собираетесь клонировать прямоугольник. Средняя линия пересечёт сторону прямоугольника в точке А.

Продолжите стороны прямоугольника в том же направлении.

Проведите через точку A линию из дальнего угла прямоугольника. Она пересечет его продлённую сторону в точке B. Точка B отмеряет ширину нового, точно такого же прямоугольника.

Теперь проведите вертикальную линию. Она станет дальней стороной нового прямоугольника.

Вы можете удваивать прямоугольники с помощью диагонали не только на плоскости, но и в перспективе. Сначала найдите центр прямоугольника, затем размножьте его во всех направлениях. Заполните всю страницу такими конструкциями.

Следует помнить, что в перспективе центр прямоугольника смещается по отношению к зрителю. Это происходит из-за схождения линий. Когда перспективное искажение небольшое (горизонт далеко по сравнению с размерами объектов), линии сходятся медленно, и центр прямоугольника смещается незначительно. И наоборот, смещение центра очень ярко выражено в случае сильного перспективного искажения.

Постройте куб. Нижняя грань параллельна земле, никаких причудливых наклонов. Затем клонируйте любую грань куба с помощью метода диагоналей. Наметьте линии, которые будут направлены в точки схода.

Помните, квадраты сжимаются сильнее по мере удаления от зрителя. Если сравнивать первый и второй квадраты, этот эффект выражен ярко. Для каждого последующего квадрата он менее очевиден, но присутствует всегда.

Нарисуйте кубы один за другим. Заполните ими всю страницу.

Сквозное построение означает, что вы рисуете твердые тела так, будто они прозрачные. Так вы всегда будете знать, где именно в пространстве находятся те участки поверхности тела, которые недоступны глазу. Это поможет правильно располагать тела по отношению друг к другу.

Переходим к практике:

Нарисуйте куб способом выше, но теперь обозначьте и его невидимые рёбра тоже.

Клонируйте куб по направлению к правой точке схода. Оставьте между двумя кубами пустое пространство размером с такой же куб.

Теперь клонируйте куб в сторону левой точки схода. И снова оставьте между ними расстояние, куда мог бы поместиться третий куб.

Заполните всю страницу такими построениями, меняя ракурс и степень перспективного искажения.

Интересная деталь. Как вы могли заметить, уходя вдаль, некоторые плоскости сильнее сжимаются (мы уже знаем почему), а другие — наоборот, больше открываются зрителю.

Теперь переходим к самому интересному!

Шаг 1. Нарисуйте эллипс. Он может располагаться на любой грани куба. Здесь вас должны волновать только сжатие и направление нормали.

Шаг 2. Проведите нормальную линию исходя из того, как вы хотите развернуть ближайшее к зрителю ребро куба. Линия горизонта для этого куба фактически не будет горизонтальной. Да, получился немного каламбур.

Какой она тогда должна быть? Просто перпендикулярной нормали нашей плоскости. Это единственное требование.

Шаг 3. Определитесь с силой перспективного искажения. В нашем случае линия горизонта находится за пределами холста, поэтому оно выражено слабо.

Шаг 4. Определите правильную длину «вертикального» ребра куба, используя эллипс или просто на глаз. Проведите линию к правой точке схода, чтобы закрыть грань снизу.

Шаг 5. Последняя грань сама станет на место. Просто постройте правильные параллельные линии к тем, которые уже есть.

Масса — это простое сферическое или колбасоподобное тело, используемое в качестве основы для построения сложных форм. Думайте о ней как о комке глины, существующем в трехмерном пространстве.

Используя массы, легче воссоздать чувство размера в рисунке. Они же помогут решить проблемы перспективного искажения и наложения объектов друг на друга. Как видите, метод масс работает со всеми тремя ключевыми компонентами глубины в вашем рисунке.

Давайте теперь создадим куб из сферической массы. Независимо от того, как он развернут, куб идеально вписывается в сферу.

Нарисуйте круг.

Постройте куб, используя знания, усвоенные из предыдущих блоков. Разворачивайте его как хотите, просто попробуйте соотнесите друг с другом его рёбра внутри массы.

Прямо сейчас нарисуйте целую страницу кубов, вписанных в сферы. Меняйте размер и ракурс.

Основная идея: каждая масса имеет центр. Центр сферической (или яйцеобразной) массы всегда совпадает с ее геометрическим центром. Давайте построим несколько одинаковых по размеру масс с равными промежутками между ними.

Постройте ряд одинаковых прямоугольников. Поставьте точку в центре каждой горизонтально расположенной стороны. Эти точки и будут центрами сферических масс.

• Нарисуйте сферу вокруг каждой точки. Контур каждой сферы должен касаться линий, которые направлены в центральную точку схода, — если вы хотите, чтобы сферы были одинакового размера.

Встройте кубы внутрь сферических масс. Разворачивайте их, как хотите, они всё равно будут одного размера, и расстояния между их центрами будут одинаковыми.

• Нарисуйте на земле квадрат, затем проведите внутри него прямую линию. Эта линия представляет собой расстояние между двумя кубами. Обозначьте точку схода, в которую направлена линия.

Постройте вертикальную плоскость от исходной прямой. Верхние углы этой плоскости будут центральными точками наших масс.

Нарисуйте первую сферу и линию к точке схода так, чтобы она касалась контура сферы. Эта же линия должна касаться и контура второй сферы.

Впишите куб в каждую массу, как в предыдущем упражнении.

Для начала вспомним про диагонали и построим с помощью них кривую в перспективе. Вот, как это сделать.

Проведите произвольную кривую внутри него.

Нарисуйте диагонали и средние линии квадрата. Это прямоугольное построение поможет вам перенести кривую в перспективу.

На новом слое с помощью эллипса определите, как будет выглядеть квадрат в перспективе. Проведите линию горизонта.

Нарисуйте квадрат в одноточечной перспективе, где линии параллельны либо картинной плоскости (тогда они вообще не сходятся), либо лучу зрения. Те, которые параллельны лучу зрения, сходятся в центре линии горизонта. Эта точка называется центральной точкой схода, как вы, возможно, помните. Это самый простой способ нарисовать прямоугольник.

Затем проведите диагонали и средние линии. Они будут служить вашим ориентиром.

Перенесите точки пересечения кривой с этими линиями из вашего ортографического рисунка. Например, если кривая касается верхней стороны квадрата по центру, она будет делать то же самое и в перспективе.

Нарисуйте несколько кривых этим способом и заполните всю страницу такими построениями.

Наша цель — построить кубы одинакового размера с одинаковым расстоянием между ними, но расположенные на неправильной траектории.

Проведите кривую в перспективе.

Отметьте на кривой точки, соблюдая равные интервалы между ними. Каждая точка соответствует центру массы. Определите размеры масс, которые находятся далеко от зрителя. Тогда вам будет легче определить на глаз размеры масс, расположенных в промежутках.

Заполните всю длину кривой такими сферами.

Теперь можно начинать рисовать внутри масс кубы. Поворачивайте их как хотите.

С разных ракурсов, в разных местах, с перекрытиями. Попробуйте разную силу перспективного искажения. Обязательно нарисуйте, даже если считаете, что все поняли. Это ОЧЕНЬ поможет рисовать потом любые другие предметы. Верьте в практику!

Что можно сделать:

Здесь можно посмотреть еще видео по теме.

Когда разберетесь с этими упражнениями, можно попробовать порисовать технику, как в этом плейлисте ModernDayJames. Стартовать можно отсюда:

А тут рассказывают, как понимание геометрических примитивов поможет в рисовании динамичных поз:

Текст переведен авторами Smirnov School. Мы готовим концепт-художников, левел-артистов и 3D-моделеров для игр и анимации. Если придёте к нам на курс, не забудьте спросить о скидке для читателей с DTF.

Наконец-то основы основ, а не очередное «как нарисовать сову».

Drawabox.com
Тут на эту тему есть целая программа обучающая с упражнениями и возможностью получить отзыв от художника.

Комментарий удален по просьбе пользователя

Вот эти кубы нужно показывать любому, кто спрашивает: «с чего мне начать учиться рисовать». Именно эти уроки им нужны, даже если человек не может еще сформулировать, почему он не знает, с чего начинать. Когда начинаются смехуечки на тему «ну эта, бирешь и рисуешь кароче, да?», у меня зубы скрипеть начинают, потому что я сам без этих уроков страдал много лет и никто не мог мне внятно объяснить, как правильно преодолевать непонимание законов перспективы.

Сначала ты рофлишь что тебя заставляют рисовать кубы кучу времени
А потом такой «а, ну вот это куб и вот это куб, а это шар, персонаж готов»

Да нет, когда я впервые случайно на реддите нашел drawabox.com, я просто чуть не расплакался. Над этой херней я бился столько времени, и ни разу даже опытные люди не сказали мне, что нужно понимать и учить перед этой сраной совой. Я был счастлив рисовать эти сотни кубов и пузырей, потому что именно так получилось сломать эту стену непонимания перспективы, как рисовать то, что «перед тобой». Очень немногие люди способны по наитию осознать эти законы, тупо рисуя в свое удовольствие.

Drawabox действительно отлично подходит для изучения основ или перед этим лучше прочесть Додсона «ключи к рисованию»?

Не знаю про Додсона, не могу сравнивать. Но drawabox закладывает важные основы, так что можно смело с него начинать.

Вы оттачивали каждый урок или по завершению одного переходили к следующими?

Пока в голове не приходило понимание, как нужно правильно делать. Я не идеально рисую, но именно логика построения объема мне стала понятна. А так все упражнения из всех уроков желательно повторять в любое время. Там есть статья про «оттачивание». https://drawabox.com/faq/grinding

Пролистал щас этого Додсона.
Всё-таки это разные материалы. Додсон – скорее краткое пособие и рекомендации по всему одновременно: анатомии, формам, теням, объёмам. Прочитать это хозяйство будет не лишним чтобы хотя бы попробовать настроить мозг ну и может быть почерпнуть пару лайфхаков.

Кубы – это всё-таки ближе к практическим упражнениям и оттачиванию моторики, плюс закладывание рутины. Делать из drawabox всесильную панацею не стоит, но методика хороша в первую очередь энтузиастам, которые взяли вот чистый листок и сидят не вдупляют хуле делать с ним. Прогресс в рисовании – это в первую очередь нон-стоп задрачивание скилла. Поэтому, если хочешь начать рисовать как хобби, в свободное время просто пролистай этого Додсона, Лумиса и прочих из списка кого там советуют, настройся, и начни регулярно хотя бы вот этот Drawabox, постепенно начиная обмазываться анатомией, артбуками профессионалов, которым хочешь подражать, собирать альбом референсов и тп.

Как человек, который прорисовал коробки, который выдрачивал коробки днями и свято верил в успех — лучше начать с Додсона. Дравбокс даёт несколько другой материал, все же сначала нужно научиться рисовать с натуры, т. е. как видишь, а не как знаешь. После Додсона, которого я взял *относительно* поздно в своём пути, стало гораздо легче.
Очевидно на звание профессионального творца не претендую, просто делюсь опытом.
Упражнения на линии из Дравбокса, кстати — тема. Уметь проводить линии от плеча надо

Так, приличные уроки от Сида Мида, одобряю!

🔍 Видео

Как нарисовать куб | Простой рисунок кубаСкачать

Как рисовать куб. Урок 79Скачать

ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать

Как нарисовать ШАР (сфера). Построение , штриховка.Скачать

КАК НАРИСОВАТЬ КУБ | Для новичковСкачать