Согласно определению (а, b) = | а | ∙ | b | ∙ cos φ, где φ – угол между векторами а и b. Из этой формулы получаем: cos φ = 
cos φ = 
Пример. Найти угол между векторами а = 2i – 4 j + 4k и b = -3i + 2 j + 6k.
cos φ = 

Пусть b = i, т.е. b = . Тогда для всякого вектора а = <x, y, z> ≠ 0 имеем



















где α – угол, образованный вектором ас осью Ох.
Аналогично получаем формулы
cos β = 



Данные формулы определяют направляющие косинусы вектора а, т.е. косинусы углов, образуемых вектором ас осями координат (рис.29).
Пример. Найти координаты единичного вектора n 0 .
По условию | n 0 | = 1. Пусть n 0 = xi+ y j + zk. Тогда (n 0 , i) = x = | n 0 | ∙ | i | ∙ cos (n 0 ^ i) = cos α,
(n 0 , j) = y = cos β, (n 0 , k) = z = cos γ .
Т.о., координатами любого единичного вектора являются косинусы углов, образованных этим












Отсюда получаем: (n 0 ) 2 = (n 0 , n 0 ) = 1 = cos 2 α+ cos 2 β + cos 2 γ.
Пример. Пусть единичный вектор n 0 ортогонален оси Оz: n 0 = xi+ y j (рис.30).
Тогда его координаты соответственно равны x= cos φ, y= sin φ. Тем самым,
n 0 = i cos φ+ j sin φ.
Векторное произведение векторов










1) длина вектора [а, b] равна | а | ∙ | b | ∙ sin φ, где φ – угол
между векторами а и b (рис.31);
2) вектор [а, b] перпендикулярен векторам а и b, т.е.
перпендикулярен плоскости этих векторов;
3) вектор [а, b] направлен так, что из конца этого вектора Рис.31.












часовой стрелки (рис.32). Иными словами, векторы а, b и [а, b]
образуют правую тройку векторов, т.е. расположены так, как
большой, указательный и средний пальцы правой руки.
В случае, если векторы а и b коллинеарны, считаем, что [а, b] = 0.
По определению длина векторного произведения Рис.32.







численно равна площади Sп параллелограмма (рис.33), построенного
на перемножаемых векторах а и b, как на сторонах | [а, b] | = Sn
5.1. Свойства векторного произведенияРис.33.
- Векторное произведение равно нулевому вектору тогда и только тогда, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы коллинеарны (если векторы коллинеарны, то угол между ними равен либо нулю, либо π).
- Это легко получить из того, что | [а, b] | = | а | ∙ | b | ∙ sin φ.














- Векторное произведение антикоммутативно [а, b] = –[b, а] . (2)
же их противоположны, т.к. из конца вектора [а, b] кратчайший поворот от а к b
будет виден происходящим против часовой стрелки, а из конца вектора [b, a] – по
часовой стрелке (рис.34).
- Векторное произведение обладает распределительным свойством Рис.34.
относительно сложения: [а + b, c] = [a, c] + [b, c] .
- Числовой множитель λ можно выносить за знак векторного произведения:
[λа, b] = [a, λb] = λ[a, b] .
- Лекция Применение векторов для вычисления величин углов и расстояний
- «Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Проекция вектора на ось, свойства проекций. Направляющие косинусы.
- 🎥 Видео
Видео:Косинус угла между векторами. Коллинеарность векторовСкачать

Лекция Применение векторов для вычисления величин углов и расстояний
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
ТЕМА 7.4 УГОЛ МЕЖДУ ВЕКТОРАМИ. УГОЛ МЕЖДУ ВЕКТОРОМ И ОСЬЮ
Содержание учебного материала:
Применение векторов для вычисления величин углов и расстояний:
1.Понятие угла между векторами.
2.Формула вычисления угла между векторами.
3.Понятие направляющих косинусов вектора.
4.Формулы вычисления направляющих косинусов вектора.
1.Понятие угла между векторами.
Угол между векторами — это угол между их направлениями (рис.1).
Угол между сонаправленными векторами равен 0.
Угол между противоположно направленными векторами равен
Угол между ортогональными векторами равен.
2. Формула вычисления угла между векторами.
Из определения скалярного произведения векторов находим угол
Пример 1. Найдите угол АСВ в треугольнике АВС, если, В(-2;0;7) и
Решение. 1. Угол АСВ в треугольнике АВС находится между векторами
и Определим координаты векторов:.
2. Найдём угол между векторами и по формуле (1) , подставив в неё соответствующие координаты:
3. Определим величину искомого угла по таблице значений тригонометрических функций или с помощью калькулятора:
Итак, угол между векторами и найден: .
3.Понятие направляющих косинусов вектора.
4.Формулы вычисления направляющих косинусов вектора.
Определим углы, составляемые вектором AB = (x; y; z) с координатными осями:
Пример 2 . Найти углы, составляемые вектором с координатными осями, если
1. Найдём координаты вектора:
2.Вычислим длину вектора:
3. Определим углы, составляемые вектором с координатными осями:
Итак, углы, составляемые вектором с координатными осями, равны
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 943 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 679 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 306 человек из 67 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Угол между векторами | МатематикаСкачать

Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 501 671 материал в базе
Материал подходит для УМК
«Геометрия. Базовый и углубленный уровни», Нелин Е.П., Лазарев В.А.
§ 27. Применение метода координат и векторов к решению стереометрических задач
Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Другие материалы
- 09.06.2018
- 1259
- 09.06.2018
- 5268
- 09.06.2018
- 695
- 09.05.2018
- 1061
- 09.04.2018
- 754
- 03.04.2018
- 2190
- 28.02.2018
- 185
- 09.02.2018
- 5765
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.06.2018 683 —> —> —> —>
- DOCX 85.6 кбайт —> —>
- Оцените материал:
Настоящий материал опубликован пользователем Карсакова Елена Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 7 лет и 11 месяцев
- Подписчики: 26
- Всего просмотров: 60307
- Всего материалов: 33
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Построение проекции вектора на осьСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Новые курсы: педагогический дизайн, ФГОС третьего поколения, управление школой и другие направления подготовки
Время чтения: 14 минут
Большинство российских школьников недовольны качеством питания в столовых
Время чтения: 1 минута
Учителя и воспитатели детсадов Подмосковья будут получать дополнительно 5 тыс. рублей
Время чтения: 1 минута
Санкт-Петербургский госуниверситет переходит на дистанционное обучение
Время чтения: 1 минута
В Петербурге введут новые COVID-ограничения для несовершеннолетних
Время чтения: 2 минуты
Минспорта утвердило программу подготовки киберспортсменов
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Как находить угол между векторамиСкачать

Проекция вектора на ось, свойства проекций. Направляющие косинусы.
Читайте также:
|























 M1 N
M1 N (4)
(4)
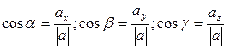 (5)
(5)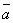 на ось l равна произведению модуля вектора
на ось l равна произведению модуля вектора 
 .
. получаем
получаем  . Откуда
. Откуда  или
или 

 .
. .
. имеет то же направление, что и
имеет то же направление, что и  .
. .
.












