Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин
Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.
Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.
- Центры тяжести многоугольников и многогранников
- Двумерный случай: многоугольники
- Центр масс системы точек
- Центр масс каркаса
- Центр масс сплошной фигуры
- Случай треугольника
- Случай треугольника: доказательство
- Случай многоугольника
- Случай многоугольника: альтернативный способ
- Трёхмерный случай: многогранники
- Центр масс системы точек
- Центр масс каркаса многогранника
- Центр масс поверхности многогранника
- Центр масс сплошного многогранника
- Случай тетраэдра
- Случай произвольного многогранника
- Центр треугольника
- Как найти центр треугольника
- 🎥 Видео
Видео:Уравнения стороны треугольника и медианыСкачать

Центры тяжести многоугольников и многогранников
Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.
Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.
В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.
Видео:9 класс, 11 урок, Формулы для вычисления координат точкиСкачать

Двумерный случай: многоугольники
На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:
- Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
- Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
- Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.
Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.
Центр масс системы точек
Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:
где 


В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:
Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке 

и, выражая отсюда 
Центр масс каркаса
Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.
Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.
Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:
где 




Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).
Центр масс сплошной фигуры
Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.
Случай треугольника
Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:
Случай треугольника: доказательство
Приведём здесь элементарное доказательство, не использующее теорию интегралов.
Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian «Finding Centroids the Easy Way».
Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.
Разобьём данный треугольник 
Четыре получившихся треугольника подобны треугольнику 

Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого 


Пусть теперь вектор 





Наша цель — показать, что вектора 

Обозначим через 






Искомый центр масс 




Таким образом, вектор от вершины 





Таким образом, мы доказали, что вектора 



Более того, попутно мы доказали, что центроид делит каждую медиану в отношении 
Случай многоугольника
Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.
Окончательная формула получается следующей:
где 



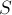
Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники 

Случай многоугольника: альтернативный способ
С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка 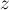


где 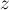
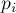




Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Трёхмерный случай: многогранники
Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:
- Центр масс системы точек — вершин многогранника.
- Центр масс каркаса — рёбер многогранника.
- Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
- Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.
Центр масс системы точек
Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:
который в случае равных масс превращается в среднее арифметическое координат всех точек.
Центр масс каркаса многогранника
Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.
Центр масс поверхности многогранника
Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.
Центр масс сплошного многогранника
Случай тетраэдра
Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.
Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).
Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.
Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:
(это можно вывести из того факта, что центроид делит медианы в отношении 
Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.
Случай произвольного многогранника
Перейдём теперь к общему случаю — случаю произвольного многогранника.
Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.
Видео:Вычисляем высоту через координаты вершин 1Скачать

Центр треугольника
Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.
Существует несколько понятий центра для треугольника.
Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.
Ортоцентр — точка пересечения его высот.
Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.
Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).
Видео:Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

Как найти центр треугольника
Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.
Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.
Центр равностороннего треугольника является также центром вписанной и описанной окружности.
Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.
Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:
- ввести в поле калькулятора координаты вершин треугольника;
- нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.
🎥 Видео
Формула для биссектрисы треугольникаСкачать

Длина медианы треугольникаСкачать

Формулы для медианы треугольникаСкачать

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

Полярная система координатСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Координаты вектора в пространстве. 11 класс.Скачать

Видеоурок "Преобразование координат"Скачать

Определение координат центра тяжести сложной фигуры (плоского сечения)Скачать

Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Нахождение длины отрезка по координатамСкачать

99. Формулы для вычисления координат точкиСкачать

Медиана, высота и биссектриса треугольника. Центроид, инцентр, ортоцентр. Геометрия 7 класс.Скачать

Формулы для вычисления координат точки | Геометрия 7-9 класс #94 | ИнфоурокСкачать













