Колесо круг или окружность (3 видео) | Курс школьной геометрии

Что такое окружность и круг, в чем их отличия и примеры данных фигур из жизни

Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, что такое окружность и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку. Дети данную тему любят по причине ее простоты.

Содержание

Что такое окружность?
Что такое круг?
Примеры круга в реальной жизни
Отличия окружности от круга
Что такое сектор?
Выводы
Чем отличается окружность от круга
Ресурсы:
Урок геометрии по теме «О колесе и не только о нем». 6-й класс
Ход урока
1. Оргмомент, вхождение в тему.
2. Актуализация знаний.
3. Разминка.
4. Практическая работа.
5. Постановка проблемных вопросов.
6. Историческая справка.
7. Проект учащихся «Треугольник Рело».
8. Домашнее задание.
9. Подведение итогов урока.
🔥 Видео

Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Что такое окружность?

Окружность — это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.

Видео:Длина окружности. Математика 6 класс.Скачать

Что такое круг?

Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые — кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг — это часть поверхности, очерченная окружностью.

У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый — это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).

Ну и наконец, третья характеристика, присущая кругу — это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий. В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.

Видео:Окружность и круг, 6 классСкачать

Примеры круга в реальной жизни

На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга — это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.

Да, сама звезда Солнце — это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Отличия окружности от круга

Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.

Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность — это граница круга. Вот чем отличается окружность от круга.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

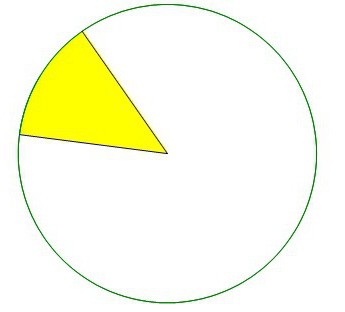
Что такое сектор?

Сектор — это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.

Предмет, отображаемый этим понятием, может иметь только круг. Окружность (радиус тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.

Видео:Чем отличается круг от окружностиСкачать

Выводы

Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих геометрических фигур, является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг — фигура капризная. Но, как говорится, тяжело в учении — легко в бою. Да, геометрия — наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.

Видео:Радиус и диаметрСкачать

Чем отличается окружность от круга

В обычной жизни нам приходится замечать множество предметов, которые по своей форме напоминают окружности и круги, но редко кто задумывается о том, чем окружность отличается от круга и что у них общего.

Окружность – это замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Окружностью называют линию, которая ограничивает круг. Правильную окружность можно изобразить с помощью циркуля. Ножку с иголкой нужно установить в задуманную точку, и тогда ножка с карандашиком начертит замкнутую линию. Эта линия разделяет плоскость на две части: внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, т. к. плоскость в общем понимании не имеет границ. Для отличия, можно заштриховать внутреннюю область. Часть, которая осталась внутри, называется кругом.

Окружность имеет центр — это начальная точка нарисования циркулем. Если задуманная точка лежит на окружности, это означает, что она ей принадлежит. Можно обозначить дуги окружности, ими будут любые 2 точки, ограничивающие окружность, т. е. любые две точки A и B окружности разбивают ее на две части; каждая из этих частей и называется дугой. Если провести линию через эти точки, то получим хорду. А хорда, проходящая через центр окружности, имеет название диаметра. Если же от центра провести линии к точке на окружности, то получится радиус окружности.

Круг – является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Пространство, закрепленное границей, включая центр круга принадлежит кругу. Если провести линию от одной точки на границе круга до другой через центр, то такое расстояние будет называться диаметром круга. Если от центра круга провести прямую линию до любой отметки на его границе, то это расстояние называется радиус. Два радиуса, равноудалённые от центра круга, будут соответствовать его диаметру. Следовательно, диаметр в два раза больше радиуса. Если от одной точки круга провести хорду, то хорда и соответствующая ей дуга будет образовывать сегмент круга. Окружность и круг имеют общий радиус и диаметр.

Отличие окружности и круга

Окружность, как любая линия имеет длину, а круг, как любая геометрическая фигура имеет площадь. Круг имеет площадь, но её нет у окружности. Круг содержит центр окружности, а окружность, содержит сам круг. Без окружности не было бы круга, но она существует самостоятельно. Окружность проводит границу круга снаружи, а круг – внутренняя часть окружности. И круг, и окружность имеют одинаковый центр.

Выводы:

Окружность представляет собой замкнутую линию.
Круг, это пространство, ограниченное окружностью.
Радиус окружности, равен радиусу круга.
Диаметр делит окружность и круг на два равных полукруга.
Окружность является границей круга.
Если начертить заштрихованную окружность, то её можно считать кругом и наоборот.
Круг и окружность имеют единый центр.
У окружности есть длина, а у круга её нет.

Ресурсы:

Большой энциклопедический словарь (БЭС)

Окружность – это замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности)

Видео:5 класс, 22 урок, Окружность и кругСкачать

Урок геометрии по теме «О колесе и не только о нем». 6-й класс

Разделы: Математика

Класс: 6

Цели и задачи урока:

повторение и закрепление математических понятий по теме «Окружность»;
расширение и формирование новых знаний по теме;
умение решать задачи по данной теме.

развитие практических навыков решения геометрических задач;
развитие практических умений и навыков в использовании чертёжных инструментов при решении задач;
развитие памяти, внимания, логического мышления.

активизация познавательной деятельность учащихся;
продолжение формирования культуры общения и коммуникативных умений учащихся.

План урока:

Оргмомент, вхождение в тему.
Актуализация знаний.
Разминка.
Практическая работа.
Постановка проблемных вопросов.
Историческая справка.
Проект учащегося «Треугольник Рело».
Домашнее задание.
Подведение итогов урока.

Видео:Окружность. Круг. 5 класс.Скачать

Ход урока

1. Оргмомент, вхождение в тему.

Приветствие, объявление темы урока: «О колесе, и не только о нем».

Ребята, как такое может быть: Три черепахи Ася, Валя, и Светлана ползут по дороге: «Я ползу первой», – с гордостью заявляет Ася. «Как хорошо, что я не последняя», – размышляет Валя. «Главное, что я обогнала Асю», утверждает Светлана.

Черепахи ползут по окружности.

Объявление целей урока.

2. Актуализация знаний.

Проведем устный опрос по теме. На экране будут появляться элементы окружности (круга). Вам нужно их узнать и дать им определения.

Окружность – множество точек на плоскости, равноудаленных от данной точки – центра окружности.

Радиус – это отрезок, соединяющий центр окружности с любой точкой окружности.

Хорда – это отрезок, соединяющий две точки окружности.

Диаметр – это отрезок, соединяющий две точки окружности и проходящий через ее центр.

Дуга – это часть окружности, ограниченная двумя точками.

Касательная к окружности – это прямая, имеющая с окружностью одну общую точку.

Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Две окружности могут касаться внешним и внутренним образом.

Точки касания окружностей лежат на прямой, проходящей через центры этих окружностей.

Круг – это множество точек, расположенных на расстоянии, не большем данного.

Ребята, как называется инструмент для черчения окружностей и дуг?

Инструмент для черчения окружностей и дуг называется циркулем.

Слово циркуль образовано от лат. circulus — круг, окружность.

А можете ли вы ответить, что общего между циркулем и цирком?

В цирке круглая арена, а циркулем чертят круги.

Правильно. Слово ЦИРК также образовано от латинского слова circus – круг.

Давайте вспомним, как безопасно пользоваться циркулем, ведь он – колющий предмет.

А у всех ли есть циркули? Покажите их мне!

3. Разминка.

Сейчас для разминки мы проведем такую работу: с помощью циркуля нарисуем цветок. У доски работают три человека, остальные – на местах.

Какие красивые цветы распустились у нас!

4. Практическая работа.

Теперь применим наши знания теоретического материала и умение пользоваться циркулем при решении задач.

Задача 1.

Начертите окружность с радиусом 4 см. Разделите ее на 6 равных частей. Найдите периметр многоугольника, образованного точками на окружности.

(один ученик работает у доски)

Задача 2. (работа в парах)

Начертите окружность с центром в точке А и с радиусом 2 см. Начертите окружность с центром в точке В, которая расположена на расстоянии 5 см от А так, чтобы она касалась первой окружности. Найдите расстояние от точки В до точек касания.

Давайте вспомним, что называют серединным перпендикуляром к отрезку?

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину отрезка и перпендикулярная к нему.

Есть свойство серединного перпендикуляра к хорде окружности:

Серединный перпендикуляр к хорде проходит через центр окружности.

А где лежит центр окружности? В середине диаметра.

Теперь применим полученное утверждение для решения следующей задачи.

Задача 3. (работа в группах)

Ученик нарисовал на доске окружность, отметил на ней точки А, В и С и стер ее, оставив лишь эти точки. Как восстановить окружность?

Физкультминутка

5. Постановка проблемных вопросов.

В ходе урока возникли проблемные вопросы:

Какое место занимает в повседневной жизни круг (или окружность)?
Почему колеса круглые?

Давайте попытаемся ответить на них.

Для полноты картины рассмотрим слайды, которые содержат части окружности или круга:

Архитектурные здания и сооружения:

Зда́ние Гла́вного шта́ба в Санкт-Петербурге. Архитектор: К. И. Росси.
Витраж собора св. Витта. Прага
Ворота Таврического дворца. С.-Петербург
Архангельский собор. Москва
Древне-Римский Колизей
Соборная площадь. Новочебоксарск

Предметы домашнего обихода, украшения.

Издавна люди украшали себя, свою одежду и свое жилище. И многие, созданные давным-давно украшения, имели форму круга. Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры.

Различные колеса:

Колесо обозрения; колесо телеги, машины; гончарный круг.

С таким кругом, конечно, встречались все. Это канализационные люки.

Как вы считаете, почему канализационные люки делают круглыми, а не квадратными? [2]

Круглая крышка люка никогда не провалится в колодец.
Крышки круглой формы также легче всего изготавливать.
Рациональный расход материала.
Равномерное распределение нагрузки на края.
Можно катить тяжелую крышку люка.
Все транспортирующие магистрали (газовые шланги, провода, шланги под воду и пр.) имеют круглое сечение, так вот что б они не «застревали» на углах.

В этом мы можем убедиться на моделях канализационных люков круглой и квадратной формы.

6. Историческая справка.

Рассмотрим гравюру Альбрехта Дюрер. Меланхолия (1514). На ней можно увидеть много элементов круга. На переднем плане – крылатый гений. В его руках – циркуль.

Говорят, что великий немецкий художник Альбрехт Дюрер одним росчерком мог безупречно нарисовать окружность, что последующая проверка при помощи циркуля не показала никаких отклонений[2].

Одно из самых важных изобретений человечества – это обыкновенное колесо. [1] Схематически колесо можно представить как круг, через центр которого перпендикулярно его плоскости проходит ось. Вокруг этой оси колесо и вращается.

Круг – воплощение нескончаемого Времени и Пространства. [3]

Во многих государствах круг и окружность считали венцом совершенства. В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности стало толчком к возникновению колеса. Если остановится колесо, то остановится колесо Истории.

Круг – колесо – прогресс (движение вперед)

Первые колеса были предназначены для перемещения грузов.

Самые первые колеса были сделаны в Месопотамии (ныне Ирак) в 3500-3000 гг. до н. э. и представляли собой гончарный круг и тележное колесо. На рисунке изображены:

Колесо из трех частей соединенных скобами 3200 г. до н.э. в Месопатамии.[4]
Легкое колесо с четырьмя спицами. Известно, что в Египте это колесо использовалось 1500 г. до н.э.
Колесо с восьмью спицами использовалось в Древней Греции 400 г. до н.э.
Римское колесо использовалось в Древнем Риме около 100 г. до н.э.
Колесо, которое сконструировал Леонардо да Винчи (конец XV в.).
Колесо одного из первых автомобилей.

Уже в середине III тысячелетия до н. э. деревянное колесо оборачивали в кожу, а к 2000 г. до н. э. стали забивать в обод медные гвозди острием наружу – для лучшего сцепления с землей. Колеса еще сплошные, но уже не вырезанные из цельного ствола, а составные, сколоченные из трех частей. Такую древесину найти легче. Примерно тогда же люди приручают лошадь, и повозки разделяются на быстрые конные двуколки – боевые колесницы и экипажи правителя – и двухосные телеги с впряженным волом – для хозяйства.

Колесо встречается в самых ранних цивилизациях (Шумер, Египет. ), однако его не знали индейцы Америки. Кто, когда и зачем впервые придумал колесо, остается одной из самых больших загадок истории.

Схематично колесо можно представить как круг, через центр которого перпендикулярно его плоскости проходит ось. Вокруг этой оси колесо и вращается. Когда колесо катится, его ось находится на одном и том же расстоянии от поверхности дороги. Это расстояние равно радиусу колеса. Именно поэтому человек, который едет на любом колесном механизме по дороге без рытвин и бугров, не испытывает неудобств от тряски.

Траекторию фиксированной точки у окружности, катящейся по прямой, называют Циклоидой.

Посмотрим, как получена циклоида и какой она формы.

7. Проект учащихся «Треугольник Рело».

Цели проекта:

Показать существование геометрических фигур постоянной ширины, отличных от круга.
Исследовать области применения Треугольника Рело.

Учащиеся выступают с проектами, в итоге получают выводы, что треугольник Рело – плоская фигура постоянной ширины и применяется в разных областях жизнедеятельности человека. Показывают существование других геометрических фигур постоянной ширины и преимущество круга среди данных фигур.

8. Домашнее задание.

Выполните эмблему математической викторины в форме треугольника Рело.

9. Подведение итогов урока.

Подведем итоги урока.

Окружность и круг играют важную роль в повседневной жизни человека, т.к. они применяются практически во всех областях его жизнедеятельности. Поскольку круг имеет постоянную ширину, то и колеса делают круглыми. Существуют и другие фигуры постоянной ширины,

такие, как, например, треугольник Рело. Но их центры описывают сложные фигуры, что усложняет их производство.

Литература и интернет-ресурсы: