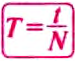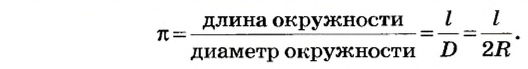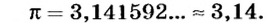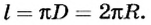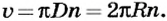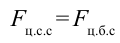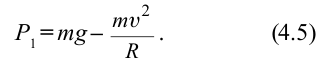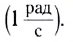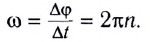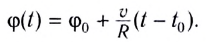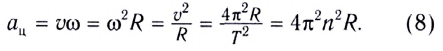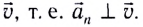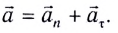Кинематические характеристики движения материальной точки по окружности

Положение частицы, движущейся по окружности, можно задать углом 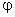, который образует радиус-вектор с каким-либо неизменным направлением, например, осью X.

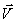
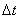
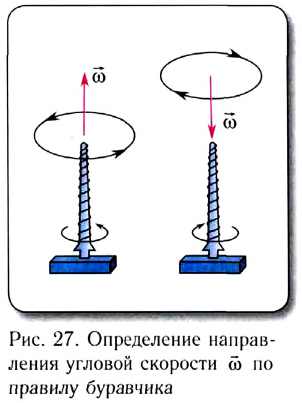
Введем для движения частицы по окружности по аналогии с линейной скоростью угловую скорость и ускорение. Угловая скорость характеризует быстроту изменения угла поворота радиус-вектора, поэтому угловой скоростью называется производная угла поворота радиус-вектора, определяющего положение материальной точки, по времени.Пусть за время точка М повернулась на угол (рис. 1.18), тогда угловая скорость

.

Направление вектора угловой скорости определяется по правилу правого винта. Если рукоятку винта поворачивать по направлению движения точки, то его поступательное движение покажет направление вектора угловой скорости.

При вращении частицы с постоянной по модулю скоростью угловую скорость называют также угловой частотой вращения. Она показывает, на какой угол поворачивается радиус-вектор, определяющий положение материальной точки, за единицу времени. Величина 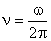дает число оборотов в единицу времени и называется частотой. Время, за которое частица совершает полный оборот, называется периодом вращения .

Вектор угловой скорости может изменяться как за счет изменения скорости вращения тела, так и за счет поворота оси вращения в пространстве. Изменение вектора угловой скорости со временем характеризуется угловым ускорением. Пусть за время вектор получает приращение . Тогда угловое ускорение определится как

.

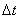
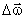
Вектор углового ускорения частицы при неизменной ориентации оси вращения параллелен этой оси и направлен вдоль вектора или против него в зависимости от того, увеличивается или уменьшается угловая скорость.

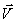
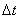
Отдельные точки вращающегося тела имеют различные линейные скорости , при этом скорость каждой из точек непрерывно изменяет свое направление. Можно показать, что модуль линейной скорости точки зависит от угловой скорости и от расстояния от этой точки до оси вращения. Пусть за малый промежуток времени тело повернулось на угол . Точка, находящаяся на расстоянии от оси вращения, проходит при этом путь . Модуль линейной скорости точки равен

.

Таким образом, модули линейной и угловой скорости связаны соотношением

.

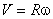
2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

«Ньютон был первым, кто попытался сформулировать элементарные законы, которые определяют временной ход широкого класса процессов в природе с высокой степенью полноты и точности, и оказал своими трудами глубокое и сильное влияние на всё мировоззрение в целом. Самой судьбой Ньютон был поставлен на поворотном пункте умственного развития человечества». А. Эйнштейн

Исаак Ньютон (Isaak Newton), 1643–1727

Выдающийся английский учёный, заложивший основы современного естествознания, создатель классической физики, член Лондонского королевского общества и его президент с 1703г. Работы Ньютона относятся к механике, оптике, астрономии, математике. В двадцать с небольшим лет Ньютон сумел заложить фундамент почти для всего существенного, что кем когда-либо было сделано.

Ньютону было свойственно исключительное трудолюбие. Отрешившись от всего, что происходит вокруг, порой без сна и отдыха, он трудился с невероятной интенсивностью. Ему понадобилось всего 18 месяцев, чтобы завершить большую часть одной из самых выдающихся книг в истории науки «Математические начала натуральной философии», которую теперь обычно называют просто «Начала». Это сочинение было написано в 1687 г. Именно в «Началах» Ньютон сформулировал закон всемирного тяготения, заложил основы классической механики и сформулировал её основные законы. Он одним из первых построил теорию движения небесных тел, создав, таким образом, основы небесной механики. Много лет спустя А. Эйнштейн, обращаясь к Ньютону, писал: «Прости меня, Ньютон: ты нашёл единственный путь, возможный в твоё время для человека величайшей научной творческой способности и силы мысли. Понятия, созданные тобой, и сейчас остаются ведущими в нашем физическом мышлении, хотя мы теперь и знаем, что если будем стремиться к более глубокому пониманию взаимосвязей, то мы должны будем заменить эти понятия другими, стоящими дальше от сферы непосредственного опыта».

Кинематика дает описание движения, не задавая вопроса о том, почему тело движется именно так, а не иначе. Динамика изучает движение тел в связи с причинами, которые обусловливают тот или иной характер движения. С точки зрения кинематики все системы отсчета равноправны, то есть выбор любой из них допустим для описания движения. Иначе обстоит дело в динамике – разделе механики, изучающем движение, основываясь на анализе его причин.

В основе классической механики лежат три закона динамики, сформулированные Ньютоном. Законы Ньютона, как и все остальные физические законы, возникли в результате обобщения большого количества опытных фактов. Правильность их подтверждается согласием с опытом тех следствий, которые из них вытекают.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Вращательное движение тела в физике — виды, формулы и определения с примерами

Содержание:

Вращательное движение тела:

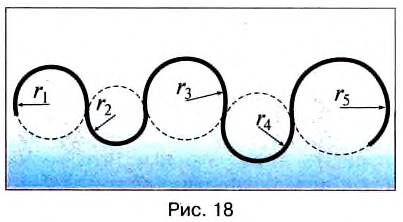
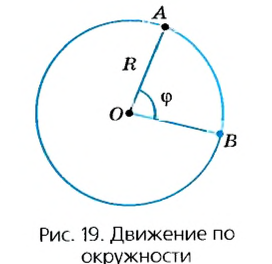
До сих пор мы изучали прямолинейное движение тел, хотя в природе и технике часто совершаются более сложные движения тел — криволинейные, когда траекторией тела является кривая линия. Любую кривую линию всегда можно представить как совокупность дуг окружностей разных радиусов (рис. 18).

Поэтому, изучив движение материальной точки по окружности, сможем в дальнейшем изучать и любые другие криволинейные движения. Кроме того, из всех возможных криволинейных движений в технике широко применяется вращательное движение деталей машин и механизмов, например вращение шестерён машин и станков, деталей, обрабатываемых на токарных станках, валов двигателей, колес машин, фрез, свёрл и т. п. Любая точка этих деталей движется по окружности. Эти две особенности и обусловили обязательное изучение движения по окружности, а именно — равномерное движение тела по окружности.

Движение материальной точки по круговой траектории с постоянной по значению, но изменяющейся по направлению скоростью, называют равномерным движением по окружности.

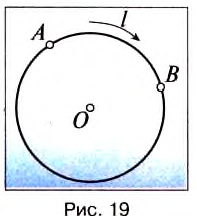
Предположим, что тело равномерно движется по окружности из точки А в точку В (рис. 19). Тогда пройденный им путь — это длина дуги

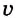
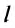
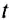
где — скорость движения тела по окружности; — пройденный телом путь (длина дуги); — время движения тела.

Направление скорости проще всего определить на опыте.

Опыт:

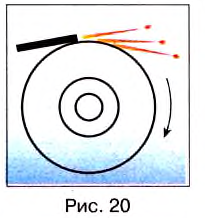
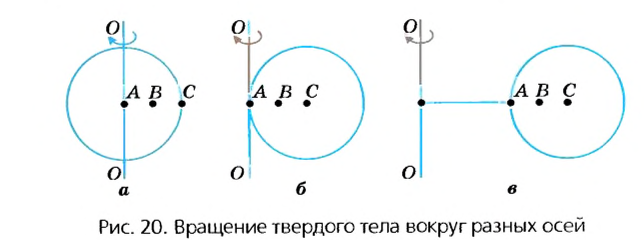
К вращающемуся точильному кругу, прикоснемся железным стержнем. Увидим, что искры из-под стержня летят по касательной к окружности этого круга (рис. 20).

Результат будет таким же в любой точке этого круга. Но каждая искра — это раскалённая частичка, оторвавшаяся от круга и летящая с такой же скоростью, какую она имела в последний момент движения вместе с кругом.

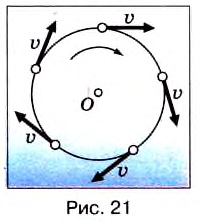
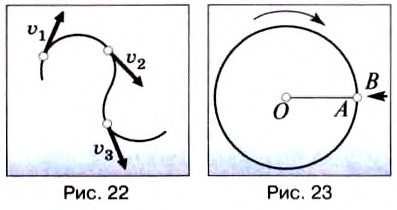
Итак, скорость материальной точки при движении по окружности направлена по касательной к ней в любой точке круга (рис. 21), а с учётом представления кривой на рисунке 18 этот вывод можно распространить на любые криволинейные движения (рис. 22).

Опыт:

Закрепим на горизонтальной оси О фанерный диск (рис. 23), на котором проведен радиус ОА. Напротив точки А поставим указатель В и будем медленно и равномерно вращать диск. Увидим, что точка А с каждым оборотом диска снова появляется напротив указателя В, т. е. совершает движение, повторяющееся через определенный интервал времени.

Движения, при которых определенные положения материальной точки повторяются через одинаковые интервалы времени, называют периодическими движениями.

Равномерное движение по окружности — это периодическое движение. Периодическое движение характеризуют такими величинами, как период обращения и частота обращения.

Период обращения — это интервал времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности.

Обозначается период обращения большой латинской буквой Т.

Если за время 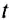материальная точка при равномерном движении по окружности совершает N оборотов, то период обращения определяется формулой:

Единицей периода обращения в СИ является одна секунда (1 с).

Если период обращения равняется 1 с, то материальная точка при равномерном движении по окружности осуществляет один оборот за 1 с.

Частота обращения определяется числом оборотов, которое материальная точка совершает за единицу времени при равномерном движении по окружности

Обозначается частота обращения малой латинской буквой .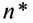

* В научной и учебной литературе частоту обращения еще обозначают малой греческой буквой 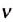(ню).

Если за время материальная точка совершила N оборотов, то, чтобы определить частоту обращения , нужно N поделить на , т. е.:
а так как = ТN , то .
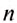
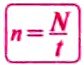
Из последней формулы видно, что частота обращения и период обращения связаны обратно пропорциональной зависимостью, а для определения единицы частоты обращения нужно единицу разделить на единицу периода обращения, т. е. на секунду.

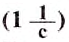
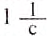
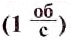
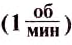
Единицей частоты обращения в СИ является единица, разделённая на секунду . это частота обращения, при котором за 1 с материальная точка совершает 1 полный оборот, двигаясь равномерно по окружности. В технике такую единицу иногда называют одним оборотом в секунду , часто применяют также единицу один оборот в минуту .

Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Движение точки по окружности

Движения, происходящие в природе и технике, могут отличаться по изменению значения скоростей и по изменению направления скоростей. Так, например, при движении точки вдоль прямой линии в одном направлении направление скорости не меняется, хотя ее значение может быть различным. В этом случае движение считается неравномерным.

Но движения могут быть и криволинейными, например, точки могут двигаться по окружностям. На рисунке 18 изображена траектория движения точек нити или ленты между круглыми барабанами. Такие траектории можно представить в виде отрезков прямых линий и окружностей разных размеров. Понятно, что такие движения могут быть и равномерными, каждая точка все время будет иметь одинаковую скорость по значению, хотя направление скорости от точки к точке траектории может меняться.

Рассмотрим движение материальной точки по окружности, когда это движение равномерно, т. е. значение скорости остается постоянным (рис. 19). Точка, двигаясь по окружности радиуса R, за определенное время 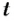переходит из точки А в точку В. При этом отрезок OA поворачивается на угол — угловое перемещение точки. Такое движение можно характеризовать угловой скоростью:

где 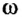(греческая буква «омега») — угловая скорость; (греческая буква «фи») — угловое перемещение.

Угловое перемещение определяется в радианах (рад.). 1 радиан — это такое перемещение, когда траектория движения точки — длина дуги окружности АВ — равна длине радиуса R.

Единицей угловой скорости является радиан в секунду (рад/с).

1 рад/с равен угловой скорости такого равномерного движения по окружности, при котором за 1 с осуществляется угловое перемещение 1 рад.

При определении угловой скорости слово «рад» обычно не пишут, а просто обозначают 1/с (имеется в виду рад/с).

Движение точки по окружности (и вращение твердого тела) характеризуют также такие величины, как период и частота вращения.

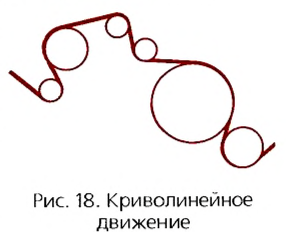
Период вращения (Т) — это время, на протяжении которого точка (тело) совершает один полный оборот по окружности. Период вращения:

где t — время вращения, N — количество выполненных оборотов.

Период вращения Т измеряется в секундах. Период равен 1 с, если точка (тело) осуществляет один оборот в секунду. Частота вращения (вращательная частота):

где N — количество совершенных оборотов за время t .

Частота вращения измеряется в оборотах за секунду (об/с).

Частота вращения определяет количество оборотов точки (тела) вокруг центра (оси вращения) за 1 с.

Еще Архимед установил, что для всех окружностей любого радиуса отношение длины окружности к его диаметру является величиной постоянной. это число обозначили греческой буквой 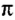(«пи»).

Таким образом, длина окружности

За один оборот материальная точка осуществляет угловое перемещение 2 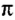рад.

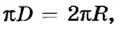
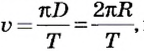
Движение по окружности характеризуется привычным для нас понятием скорости как пути, который проходит точка за единицу времени. В данном случае эта скорость называется линейной. Если учитывать, что за один оборот (время Т) точка проходит путь то линейная скорость равномерного движения точки по окружности или

Вращение твердого тела

Твердые тела состоят из большого количества частичек. Абсолютно твердыми наукой считаются тела, расстояние между точками которых не изменяется во время явлений, которые с ними происходят. Однако следует иметь в виду, что абсолютно твердых тел в природе нет.

Как упоминалось в § 3, движения твердых тел бывают поступательные и вращательные. Твердые тела могут вращаться вокруг любых осей, в том числе и тех, которые проходят через их центры.

В случае а (рис. 20) ось вращения проходит через центр шара (например, вращаются колеса транспортных средств или Земля в своем суточном вращении вокруг оси). В случае в ось проходит через край шара. В случае в шар находится на определенном расстоянии от оси (например, Земля движется вокруг Солнца или Луна вокруг Земли). В некоторых случаях даже Землю и Луну можно считать материальными точками, а в некоторых случаях это сделать невозможно. Подумайте, в каких?

Что же является наиболее характерным для вращательного движения твердых тел? Очевидно, что при этом все точки этих тел в своем движении описывают окружности, центры которых находятся на осях вращения.

Понятно также, что разные точки тел за одно и то же время проходят по своим траекториям разные расстояния — чем дальше от оси вращения лежат точки, тем больше эти расстояния. Но за одно и то же время угловое перемещение всех точек одинаково. Следовательно, и угловая скорость для всех точек данного тела также будет одинаковой.

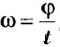
Для характеристики вращательного движения твердых тел используют такие же понятия, что и для движения точки по окружности: период вращения Т — время одного полного вращения; вращательная частота (частота вращения) 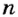— количество полных вращений за единицу времени; угловая скорость со. Кроме основной единицы частоты вращения об/с, используют об/мин, об/ч и т. п.

Период вращения Земли вокруг- Солнца равен в среднем 365 суток, а период вращения Луны вокруг Земли в среднем 28 суток. Изучая физику, астрономию, вы узнаете, что небесные тела, например планеты Солнечной системы, движутся не по окружностям, а по так называемым эллипсам.

Динамика вращательного движения

При просмотре фильмов-боевиков вы могли наблюдать, что при резком вращении руля автомобиля машина опрокидывается. В цирке мотоциклисты катаются по поверхности стен.
Проведем такой опыт. Нальем воду в ведро и раскрутим его в вертикальной плоскости. При определенной скорости вращения вода не выливается из ведра.

Из приведенных выше примеров можно сделать заключение, что существует сила, которая опрокинет машину при резком повороте, удержит мотоциклиста на стене и не даст вылиться воде из ведра при вращении.
Откуда появляется эта сила? От чего зависит ее величина?
Для этого вспомним о возникновении центростремительной силы в теле при равномерном вращательном движении:

По третьему закону Ньютона:

и при вращении появляется также центробежная сила.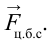
Вот эта центробежная сила опрокинет резко разворачивающуюся машину, удержит воду в ведре при вращении и т.д.

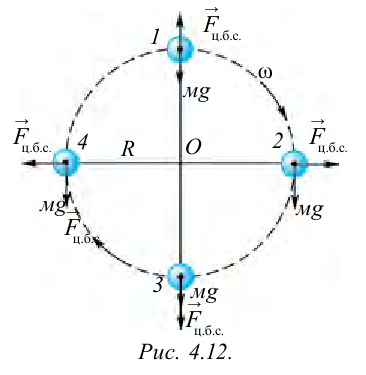
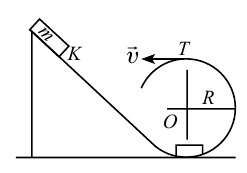
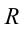
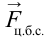
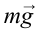
На рисунке 4.12 показаны силы, действующие на тело, которое совершает вращательные движения по кругу радиусом . В точке 1, из-за того что центробежная сила направлена противоположно силе тяжести , вес тела уменьшается:

В точке 3 сила тяжести тела и центробежная сила направлены вниз, т.е. в одном направлении. В этом случае вес тела растет:

Центробежную силу нужно учитывать при вращении тела и в случаях поворота в ходе движения.
Кроме того, на поворотах дороги под воздействием центробежной силы наблюдается отклонение тела от вертикального положения. Чтобы это не приводило к авариям, велосипедисты или мотоциклисты должны двигаться с небольшим уклоном в сторону от центра вращения (рис. 4.13а).
Для уравновешивания этой силы специально для автомобилей на поворотах строят участки дороги с уклоном с одной стороны (рис. 4.13б). Для трамваев и поездов рельсы на поворотах дороги с внешней стороны круга делаются чуть выше.

Пример

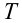
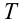
При движении по кругу тело опускается вниз. При каком радиусе круга тело не упадет с точки . Скорость тела в точке равна 30 м/с.
Дано:

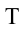
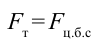
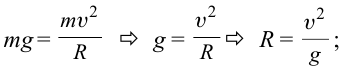
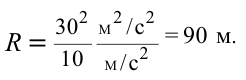
Чтобы тело не упало из точки должно выполняться следующее условие:

Ответ: 90 м.

Кинематика вращательного движения

При криволинейном движении материальной точки ее мгновенная скорость направлена по касательной к траектории в данной точке.
Движение тела (МТ) по окружности является частным случаем криволинейного движения по траектории, лежащей в одной плоскости.

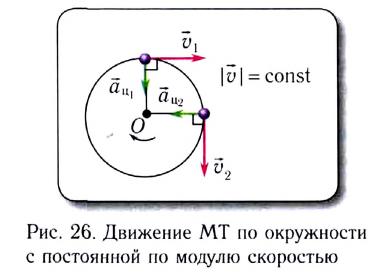
Одним из простейших и широко распространенных видов такого движения является движение по окружности с постоянной по модулю скоростью. Это такое движение, при котором тело (МТ) за любые равные промежутки времени описывает одинаковые дуги. Подчеркнем, что при подобном движении скорость точки постоянно меняет свое направление.

Для описания движения по окружности используется ряд физических величин. Рассмотрим некоторые из них.

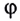
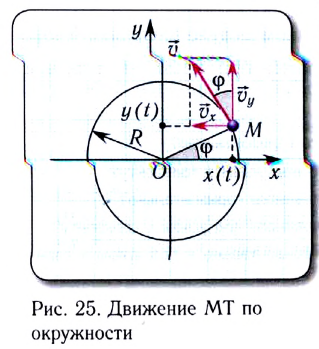
Удобным параметром для определения положения материальной точки М, совершающей движение по окружности радиусом R с центром в начале координат, является угол поворота (рис. 25)

радиус-вектора точки М. Он отсчитывается от оси Ох против хода часовой стрелки и связан с декартовыми координатами соотношениями:

По теореме Пифагора можно найти, что координаты х и у материальной точки в декартовой системе координат удовлетворяют соотношению

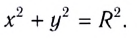
Скорость 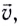с которой материальная точка движется по окружности, называется линейной скоростью (рис. 26).

Проходимый точкой путь s (длина дуги окружности) равен, как и для всякого равномерного движения, произведению модуля скорости v и промежутка времени движения

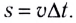
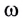
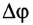
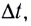
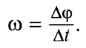
Модуль угловой скорости — это отношение угла поворота к промежутку времени за который этот поворот произошел:

Угловая скорость 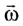со является величиной векторной. Она направлена вдоль оси вращения материальной точки, и ее направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения конца буравчика, рукоятка которого вращается в том же направлении, что и тело (рис. 27).

Единица угловой скорости в СИ — радиан в секунду

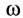
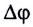
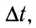
При движении по окружности с постоянной по модулю скоростью v угловая скорость является величиной постоянной и ее модуль равен отношению угла поворота к промежутку времени за который этот поворот произошел:

Здесь n — частота вращения — физическая величина, численно равная числу оборотов N материальной точки в единицу времени:

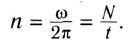
Единица частоты вращения в СИ — секунда в минус первой степени 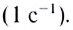Время совершения одного оборота называется периодом вращения Т.

В СИ период измеряется в секундах (1с).

При совершении полного оборота 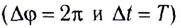период определяется по формуле

Модуль постоянной линейной скорости тела (МТ), движущегося по окружности, вычисляется по формуле

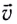
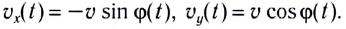
Проекции скорости (см. рис. 25) с течением времени изменяются по закону

Модуль угловой скорости определяется соотношением

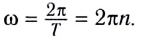
Следовательно, соотношение между модулями линейной и угловой скорости имеет вид

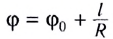
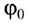
Поскольку (докажите самостоятельно), где — угол поворота радиус-вектора в момент начала движения, то кинематический закон движения МТ но окружности имеет вид

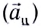
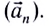
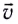
При движении МТ по окружности с постоянной по модулю скоростью ее направление непрерывно изменяется и, следовательно, движение МТ происходит с ускорением, которое называется центростремительным или нормальным Ускорение направлено по радиусу к центру окружности и характеризует быстроту изменения направления скорости с течением (см. рис. 26). Его модуль определяется формулой

Нормальное ускорение 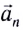в любой момент времени перпендикулярно скорости

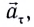
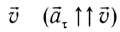
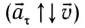
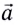
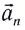
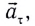
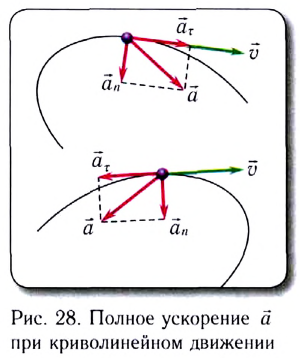
Как и при прямолинейном равноускоренном движении, ускорение называемое тангенциальным (касательным), совпадает с направлением скорости или направлено противоположно ей и поэтому изменяет только модуль скорости. Следовательно, при движении по окружности с непостоянной по модулю скоростью (например, математический маятник) или при любом криволинейном движении полное ускорение 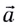можно представить в виде векторной суммы нормального ускорения и тангенциального ускорения направленного по касательной к окружности в данной точке (рис. 28):

Полное ускорение всегда направлено в сторону вогнутости траектории (см. рис. 28).

Модуль полного ускорения находится по теореме Пифагора:

где 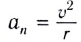— нормальное ускорение, с которым точка двигалась бы по дуге
окружности радиусом r, заменяющей траекторию в окрестности рассматриваемой точки. Этот радиус r называют радиусом кривизны траектории.

• Равномерное движение материальной точки по окружности
• Колебательное движение
• Физический и математический маятники
• Пружинные и математические маятники
• Поступательное движение
• Равномерное и неравномерное движение
• Равномерное движение
• Неравномерное движение

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Физика - движение по окружностиСкачать

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Видео:Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

🎬 Видео

Урок 7. Механическое движение. Основные определения кинематики.Скачать

Вращательное движение. 10 класс.Скачать

Поступательное и вращательное движенияСкачать

Онлайн-уроки формирования письменной деятельности (ФПД) - ОНЛАЙН-ШКОЛА Татьяны ГогуадзеСкачать

Кинематика за 8 минСкачать

Кинематика материальной точки за 20 минут (кратко и доступно) Кинематика точкиСкачать

кинематика точкиСкачать

3. Кинематика материальной точки. Угловые величиныСкачать

Урок №1 Движение материальной точки по окружностиСкачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать