Калькулятор движения по окружности (5 видео)

Рассчитать угловое ускорение, угловую скорость или время вращения при движении тела по окружности

Калькулятор рассчитывает угловое ускорение, угловую скорость или время вращения при движении тела по окружности по формулам.

Формула углового ускорения ε = dφ / dt, угловую скорость (dφ) делим на время движения (dt).

Формула угловой скорости dφ = ε * dt, угловое ускорение (ε) умножаем на время движения (dt).

Формула времени вращения dt = ε / dφ, угловое ускорение (ε) делим на угловую скорость (dφ).

Содержание

Онлайн калькулятор нахождения углового ускорения, угловой скорости или времени вращения при движении тела по окружности
Движение по окружности
Скорость при движении по окружности
Ускорение материальной точки при движении по окружности
Период и частота — характеристики равномерного движения по окружности
Примеры задач с решением
Перевести об/мин в м/с и обратно
📺 Видео

Видео:Физика - движение по окружностиСкачать

Онлайн калькулятор нахождения углового ускорения, угловой скорости или времени вращения при движении тела по окружности

Рассчитываем

Угловое ускорение (ε)

рад/сек 2

Угловая скорость (dφ)

рад/сек

Время движения (dt)

секунд

Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!

Видео:Урок 89. Движение по окружности (ч.1)Скачать

Движение по окружности

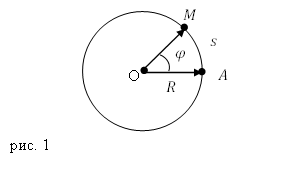
Значимым частным случаем перемещения материальной точки по заданной траектории служит движение по окружности. Местоположение точки на окружности можно задавать не при помощи расстояния от некоторой начальной точки (допустим A), а с помощью угла $varphi $, который образуют радиусы, которые провели из центра окружности (O) к рассматриваемой частице (точка M) и из О в точку начала отсчета (A) (рис.1).

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Скорость при движении по окружности

При движении по окружности вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($omega $), которая характеризует быстроту изменения угла $varphi $:

Определим, какова связь между линейной и угловой скоростями. Длину дуги АМ ($s$) (рис.1) можно найти как:

тогда изменение длины дуги за время$ Delta t$ равно$ Delta s$:

[Delta s=RDelta varphi left(3right).]

Найдем отношение $frac$, разделив обе части выражения (3) на $Delta t$:

Перейдем к пределу в правой и левой частях равенства (4) при $Delta tto 0$, получим:

Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

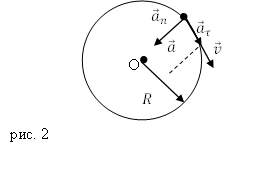
Ускорение материальной точки при движении по окружности

Величина нормальной (центростремительной) компоненты ускорения вычисляется при помощи формулы:

При равномерном перемещении по окружности величина центростремительного ускорения постоянна ($a_n=const). $Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.

Тангенциальное ускорение при движении по окружности вычисляют, как и при любом криволинейном движении:

Видео:Формулы механики 2, движение по окружности, центростремительное ускорениеСкачать

Период и частота — характеристики равномерного движения по окружности

Равномерное движение по окружности можно характеризовать при помощи такой физической величины как период обращения ($T$), который определяют как время совершения материальной точкой полного оборота. Используют и частоту ($nu$) обращения, которую определяют как величину обратную периоду, равную количеству оборотов за единицу времени:

При равномерном движении по окружности угловая скорость, частота и период связаны как:

Формула (9) дает возможность центростремительное ускорение определить как:

Отметим, что при неравномерном движении по окружности период ($T$) и частота ($nu$) свой смысл теряют, о них можно говорить только при равномерном движении по окружности.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Примеры задач с решением

Задание. Центростремительное ускорение материальной точки, перемещающейся по окружности, имеющей радиус R, задано уравнением: $a_n=A+Bt+Ct^2(frac)$. Каково тангенциальное ускорение точки? Как направлены ускорения точки?

Решение. Сделаем рисунок.

Нормальное ускорение материальной точки, движущейся по окружности можно найти как:

Следовательно, скорость точки:

Используя заданный в условии задачи закон изменения нормального ускорения $a_n=A+Bt+Ct^2(frac)$, выражение (1.3) преобразуем к виду:

Величина тангенциального ускорения определена как:

Подставим правую часть выражения (1.4) в уравнение (1.5), имеем:

Задание. Чему равен путь (s), который проходит точка в примере 1 за время $t_1$, если A= 1 $frac$, $B=6 frac$; $С=9frac$.

Решение. Путь, пройденный точкой можно найти как:

Используем выражение для величины скорости, которое мы получили в первом примере:

Подставим известные нам из условия задачи коэффициенты, преобразуем полученное выражение $v left(tright):$

Вычислим интеграл (2.1), принимая во внимание выражение (2.3):

Ответ. $s=sqrtleft(t_1+frac^2right)$

Видео:Математика это не ИсламСкачать

Перевести об/мин в м/с и обратно

Угловая скорость — это физическая величина, характеризующая скорость вращения точки вокруг центра вращения.

Линейная скорость — это физическая величина, характеризующая скорость, с которой точка движется по окружности вокруг центра вращения.

Формула перевода угловой скорости в линейную:

V = 2 * π * R * n, где

V — линейная скорость;
R — радиус окружности;
n — угловая скорость.

для справки D = 2 * R — диаметр окружности.

Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

Для сложных расчетов по переводу нескольких единиц измерения в требуемую (например для математического, физического или сметного анализа группы позиций) вы можете воспользоваться универсальными конвертерами единиц измерения.

На этой странице представлен самый простой онлайн переводчик единиц измерения м/с в об/мин. С помощью этого калькулятора вы в один клик сможете перевести об/мин в м/с (обороты в минуту в метры в секунду) и обратно.