На плоскости прямая и окружность могут либо пересекаться друг с другом, либо не пересекаться:
Расстояние от центра O до прямой m равно длине перпендикуляра OA. Следовательно, расстояние от центра окружности до прямой всегда будет равно перпендикуляру, опущенному из центра окружности на прямую.
Если расстояние от центра окружности до прямой больше радиуса данной окружности, то прямая и окружность не пересекаются и не имеют общих точек:
Видео:№631. Пусть d — расстояние от центра окружности радиуса r до прямой р. Каково взаимное расположениеСкачать

Касательная
Если расстояние от центра окружности до прямой равно радиусу данной окружности, то прямая касается окружности и они имеют одну общую точку, такая прямая называется касательной к окружности:
Прямая m — касательная. Точка соприкосновения прямой и окружности, то есть их общая точка, называется точкой касания: точка A — точка касания.
Касательная – это прямая линия, имеющая с окружностью одну общую точку.
Видео:Как найти диаметр окружности, зная длину хорды и расстояние от центра окружности до неё? #огэ #егэСкачать

Секущая
Если расстояние от центра окружности до прямой меньше радиуса данной окружности, то прямая пересекает окружность и они имеют две точки касания, такая прямая называется секущей к окружности:
Секущая – это прямая линия, имеющая с окружностью две общие точки.
Видео:Найти расстояние от центра окружности до вершины прямого углаСкачать
Взаимное расположение прямой и окружности
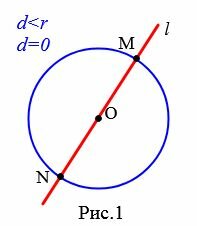
Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.
Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.
 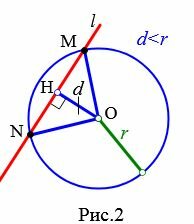 |
Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
В этом случае прямая называется секущей по отношению к окружности.
Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
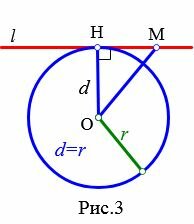 |
Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.
Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
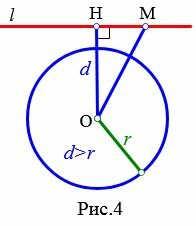 |
Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
Видео:№632. Расстояние от точки А до центра окружности меньше радиуса окружности. Докажите, что любаяСкачать

Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
📺 Видео
Расстояние между высотой и центром окружности (от точки до прямой) ОГЭ-ЕГЭСкачать

ОГЭ 2022 Демоверсия. 16 заданиеСкачать

Геометрия на ЕГЭ. Расстояние от центра окружности до произвольной точки хорды. Степень точки.Скачать

ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать

§15 Расстояние от точки до прямойСкачать

Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Прямая и окружность. Математика. 6 класс.Скачать

Планиметрия 19 | mathus.ru| расстояние от центра окружности до точки пересечения диагоналей трапецииСкачать

10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Окружность, диаметр, хорда геометрия 7 классСкачать

Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Расстояние от точки до прямой | Геометрия 7-9 класс #37 | ИнфоурокСкачать

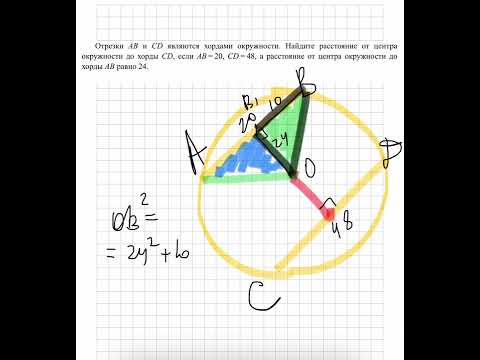
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать