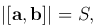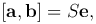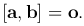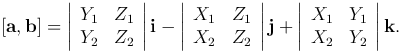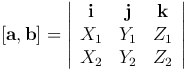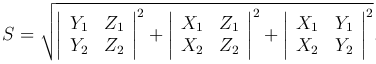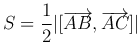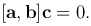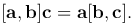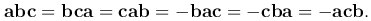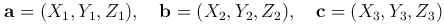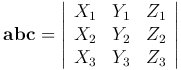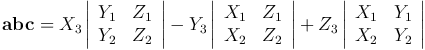§ 33. Смешанное произведение трёх векторов
Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись а, b, с означает, что вектор а считается первым, b — вторым, с — третьим.
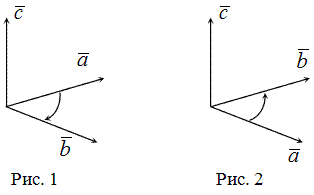
Тройка некомпланарных векторов а, b, с называется правой, если составляющие её векторы, будучи приведены к общему началу, располагающи в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы а, b, с расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.
Смешанным произведением трёх векторов а, b, с называется число, равное векторному произведению [ab], умноженному скалярно на вектор с, т. е. [ab] с.
Имеет место тождество: [ab] с = а [ab], ввиду чего для обозначения смешанного произведения [ab] с употребляется более простой символ: abc. Таким образом,
Смешанное произведение abc равно объёму параллелепипеда, построенного на векторах а, b, с, взятому со знаком плюс, если тройка abc правая, со знаком минус, если эта тройка левая. Если векторы а, b, с компланарны (и только в этом случае), смешанное произведение abc равно нулю; иначе говоря, равенство abc = 0
есть необходимое и достаточное условие компланарности векторов а, b, c. Если векторы а, b, с заданы своими координатами:
то смешанное произведение abc определяется формулой
abc =
Напомним, что система координатных осей предполагается правой (вместе с тем является правой и тройка векторов i, j, k.
865. Определить, какой является тройка а, b , с (правой или левой), если:
1) а = k, b = i, с = у; 2 )а = i, b = k, c = j;
3) a = j, b = i, c = k; 4) а = i + y, b = j, c = k;
5) a = i + j, b = i — j, c= j; 6) a = i + y, b = i — j, c = k.
866. Векторы a, b, с, образующие правую тройку, взаимно перпендикулярны. Зная, что |а| = 4, |а| = 2, |а| = 3, вычислить abc.
867 . Вектор с перпендикулярен к векторам а и b, угол между а и b равен 30°. Зная, что |а| = 6, |b| = 3, |c| = 3, вычислить abc.
868. Доказать, что
в каком случае здесь может иметь место знак равенства?
869 . Доказать тождество (а + b) (b + с) (с + а) = 2abc.
870. Доказать тождество
аb (с + l a + 
где |а| и — какие угодно числа.
871. Доказать, что векторы а, b, с, удовлетворяющие условию
872. Доказать, что необходимым и достаточным условием компланарности векторов а, b, с является зависимость



где по крайней мере одно из чисел 

873. Даны три вектора:
Вычислить a b c.
874. Установить, компланарны ли векторы а, b, с, если:
875 . Доказать, что четыре точки
А(1; 2; —1), В (0; 1; 5), С (—1; 2; 1), D (2; 1; 3)
лежат в одной плоскости.
876. Вычислить объём тетраэдра, вершины которого находятся в точках А (2; —1; 1), В (5; 5; 4), С (3; 2; — 1) и D (4; 1; 3).
877. Даны вершины тетраэдра:
А(2; 3; 1), В(4; 1;—2), С(6; 3; 7), D(— 5; —4; 8).
Найти длину его высоты, опущенной из вершины D.
878. Объём тетраэдра 
Видео:18+ Математика без Ху!ни. Векторное произведение.Скачать

Правая и левая тройки векторов
Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
любую работу
Видео:Правые и левые тройки векторовСкачать

Все еще сложно?
Наши эксперты помогут разобраться
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Правые и левые тройки векторов
Определение. Три некомпланарных вектора 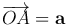
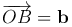
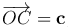
Будем смотреть с конца вектора c на плоскость, определяемую векторами a и b. Если кратчайший поворот от вектора a к вектору b совершается против часовой стрелки, то тройка векторов a, b, c называется правой, если указанный поворот совершается по часовой стрелке, тройка a, b, c называется левой. Все правые (или левые) тройки векторов называются одинаково ориентированными. Если одна тройка является правой, а другая — левой, то они называются тройками различной ориентации. Если даны три некомпланарных вектора a, b и c, то они образуют 6 троек: a, b, c; b, c; a; c, a, b имеющие одну ориентацию (круговая перестановка векторов), а b, a, c; a, c, b; c, b, a имеют другую ориентацию (перестановка двух векторов).
Определение. Декартова прямоугольная система координат называется правой, если тройка базисных векторов i, j, k является правой и называется левой, если эта тройка левая. В дальнейшем будем рассматривать только правые системы координат.
Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Векторное произведение векторов
Определение. Векторным произведение вектора a на вектор b называется третий вектор [a, b], удовлетворяющий следующим условиям:
- 1) |[a, b]|=|a| |b|sin φ, где φ — угол между векторами a и b;
- 2) вектор [a, b] перпендикулярен каждому из векторов a и b;
- 3) тройка (a, b, [a, b]) является правой тройкой.
Векторное произведение обозначают также a×b.
Из условия 1) определения следует, что
где S — площадь параллелограмма, построенного на векторах a и b. Тогда
где e — единичный вектор направления вектора [a, b].
Необходимое и достаточное условие коллинеарности двух векторов. Вектора a и b коллинеарны тогда и только тогда, когда
Доказательство. □ Если вектора a и b коллинеарны, то φ=0 или φ=π, тогда sin φ=0, следовательно, |[a, b]|=0, а значит [a, b]=o.
Обратно, если выполнено равенство [a, b]=0 и a≠0, b≠0, то φ=0 или φ=π, следовательно, вектора a и b коллинеарны. ■
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Свойства векторного произведения
- 1. [a, b]=-[b, a] (антикоммутативность);
- 2. [αa, b]=α[a, b], [a, βb]=β[a, b] (ассоциативность относительно умножения на число);
- 3. [a+b, c]=[a, c]+[b, c], [a, b+c]=[a, b]+[a, c] (дистрибутивность относительно сложения векторов).
Замечание. Эту формулу можно выразить через символический определитель третьего порядка:
Следствие. Площадь параллелограмма, построенного на векторах a и b, вычисляется по формуле
Следствие. Площадь треугольника ABC определяется формулой:
Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Смешанное произведение векторов
Теорема [геометрический смысл смешанного произведения]. Смешанное произведение [a, b]c трех некомпланарных векторов равно объему параллелепипеда, построенного на векторах 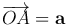
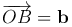
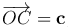
Доказательство. □Рассмотрим параллелограмм, построенный на векторах 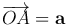
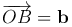
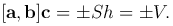
Следствие. Векторы a, b, c компланарны тогда и только тогда, когда их смешанное произведение равно нулю, то есть
Следствие. Справедливо равенство
Замечание 1. Так как верно это следствие, то смешанное произведение обозначают abc.
Замечание 2. Для трех векторов a, b, c имеем
Теорема. Смешанное произведение трех векторов
— это разложение определителя третьего порядка по элементам третьей строки. ■
Следствие [Необходимое и достаточное условие компланарности трех векторов]. Три вектора a, b, c компланарны тогда и только тогда, когда выполняется
📹 Видео
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Смешанное произведениеСкачать
§20 Нахождение объёма параллелипипедаСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Аналитическая геометрия, 3 урок, Векторное произведениеСкачать

§11 Ориентация векторов в пространствеСкачать

Угол между векторами | МатематикаСкачать

Векторное произведение векторовСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Единичный векторСкачать