Какую сторону треугольника называют гипотенузой

Что такое гипотенуза треугольника? У какого треугольника есть гипотенуза?

Гипотенуза — это сторона прямоугольного треугольника, лежащая напротив прямого угла.

Таким образом, гипотенуза есть только в прямоугольном треугольнике.

Даже если в условии задачи прямо не сказано, что треугольник — прямоугольный, но одна из его сторон названа гипотенузой, это означает, что данный треугольник имеет и прямой угол.

Если прямой угол назван одной буквой, то в названии гипотенузы этой буквы нет.

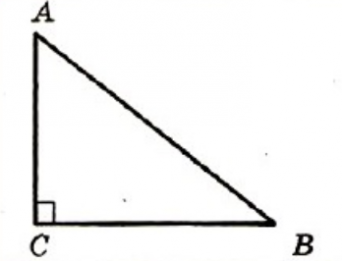
Например, в треугольнике ABC

лежит напротив прямого угла C.

(В названии гипотенузы — AB — буквы C нет).

Как правило, в условии задачи не сказано, какая сторона треугольника является гипотенузой.

Гипотенуза определяется по положению прямого угла.

Например, в треугольнике MKF

Значит, MF — гипотенуза

(поскольку она лежит напротив прямого угла K).

Гипотенуза — самая длинная из сторон прямоугольного треугольника.

Длина гипотенузы больше длины любого катета.

Согласно неравенству треугольника, длина гипотенузы меньше суммы длин катетов.

Как найти длину гипотенузы, зная катеты и один из острых углов, мы рассмотрим позже.

Видео:Теорема Пифагора для чайников)))Скачать

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

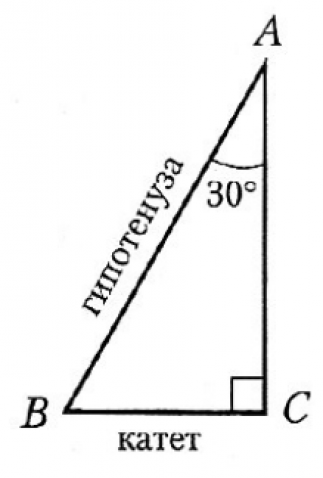
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Видео:Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Прямоугольный треугольник. Теорема Пифагора.

теория по математике 📈 планиметрия

Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Свойства прямоугольного треугольника

• В прямоугольном треугольнике гипотенуза является наибольшей стороной.
• В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .

Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .

• Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
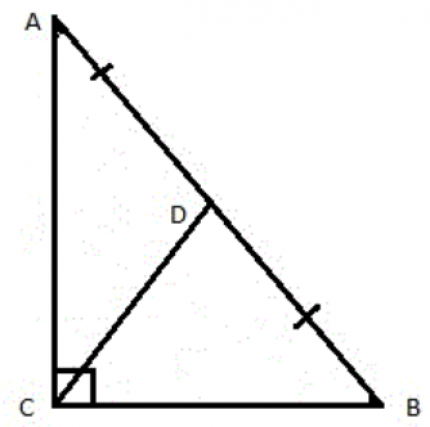
• Медиана, проведенная к гипотенузе, равна её половине.

На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

1. по катетам;
2. по катету и прилежащему острому углу;
3. по гипотенузе и острому углу;
4. по гипотенузе и катету.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

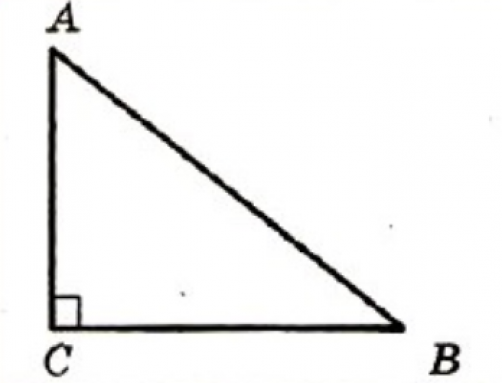
На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.

🎬 Видео

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Виды треугольниковСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Определение длины гипотенузыСкачать

Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

Чему равна гипотенуза прямоугольного треугольника, если его периметр и площадьСкачать

Что такое гипотенузаСкачать

Найдите третью сторону треугольникаСкачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать