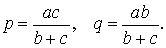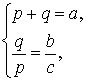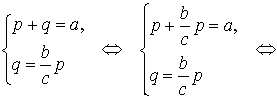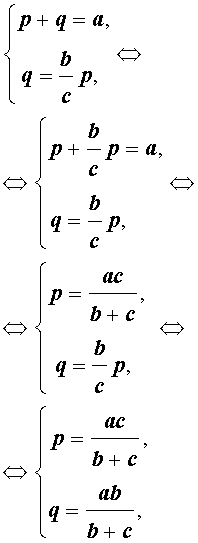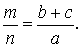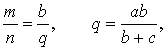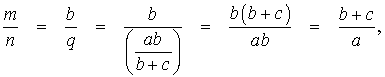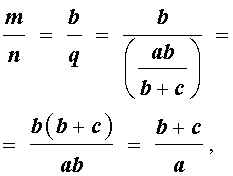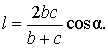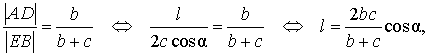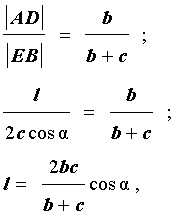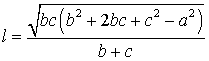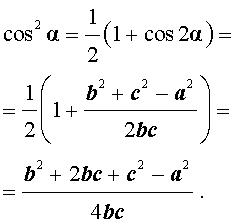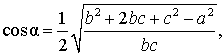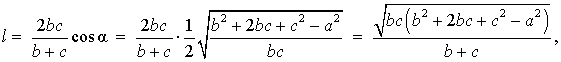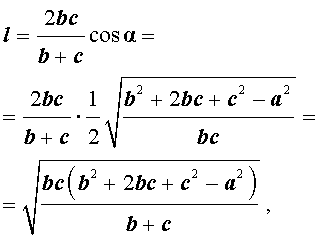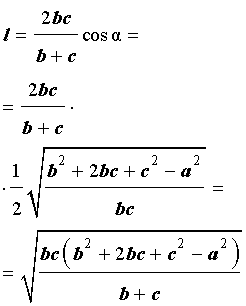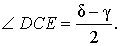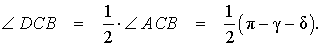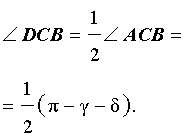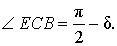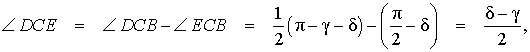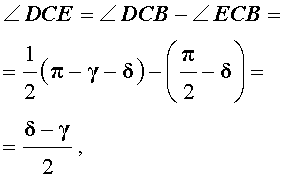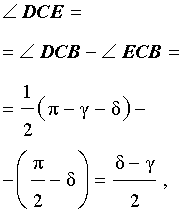Какой отрезок является биссектрисой треугольника (7 видео)

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Содержание

Определение биссектрисы угла треугольника
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Пример задачи
Биссектриса треугольника
Биссектриса — это луч разрезающий угол пополам, а также отрезок в треугольнике обладающий рядом свойств
Биссектриса — это.
Количество биссектрис в треугольнике
Пересечение биссектрис треугольника
Свойство основания биссектрисы
Биссектриса равнобедренного треугольника
Комментарии и отзывы (3)
📺 Видео

Видео:№537. Отрезок AD является биссектрисой треугольника ABC. Найдите BD и DC, если АВ = 14 смСкачать

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

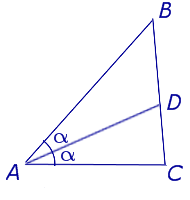
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

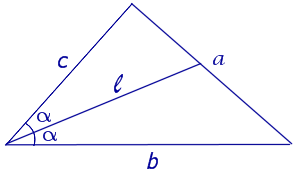
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

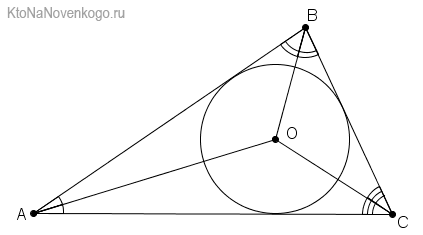
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

CD – внутренняя биссектриса ∠ACB;
CE – биссектриса угла, смежного с ∠ACB;
∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Видео:№536. Отрезок BD является биссектрисой треугольника ABC. а) Найдите АВ, если ВС = 9 смСкачать

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

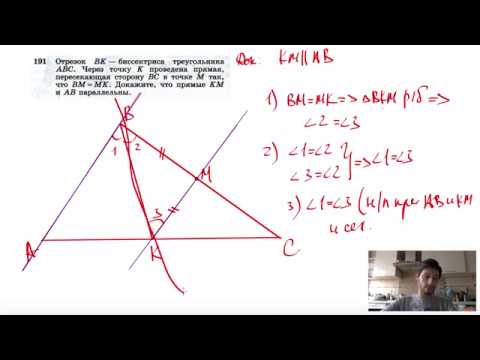
Видео:№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать

Биссектриса треугольника

Напомним, что биссектрисой угла называют луч, делящий угол пополам.

Определение . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника и соединяющий вершину треугольника с точкой на противоположной стороне (рис 1).

Поскольку в каждом треугольнике имеются три угла, то в каждом треугольнике можно провести три биссектрисы.

На рисунке 1 биссектрисой является отрезок AD .

Теорема 1 . Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.

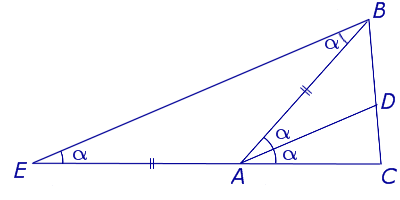
Доказательство . Продолжим сторону AC треугольника ABC , изображенного на рисунке 1, за точку A . Проведем через точку B прямую, параллельную биссектрисе AD . Обозначим точку пересечения построенных прямых буквой E (рис. 2).

Докажем, что отрезки AB и AE равны. Для этого заметим, что угол EBA равен углу BAD , поскольку эти углы являются внутренними накрест лежащими при параллельных прямых EB и AD . Заметим также, что угол BEA равен углу DAC , поскольку эти углы являются соответственными при параллельных прямых EB и AD . Таким образом, угол EBA равен углу BEA , откуда вытекает, что треугольник EAB является равнобедренным, и отрезки AB и AE равны.

Отсюда, воспользовавшись теоремой Фалеса, получаем:

что и требовалось доказать.

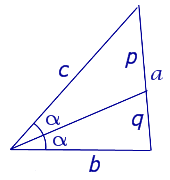
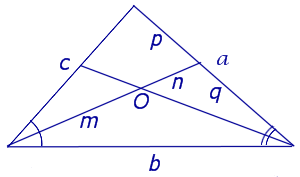
Следствие 1 . Рассмотрим рисунок 3, на котором изображен тот же треугольник, как и на рисунке 1, но для длин отрезков использованы обозначения

b = |AC|, a = |BC|, c = |AB|, p = |BD|, q = |DC|.

что и требовалось доказать.

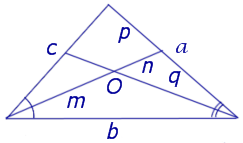
Следствие 2 . Рассмотрим рисунок 4, на котором изображены две биссектрисы треугольника, пересекающиеся в точке O .

Тогда справедлива формула:

что и требовалось доказать.

Теорема 2 . Рассмотрим рисунок 5, который практически совпадает с рисунком 2.

Тогда для длины биссектрисы справедлива формула:

Доказательство . Из рисунка 5 следует формула

Если воспользоваться этой формулой, то из подобия треугольников ADC и EBC , получаем:

что и требовалось доказать.

Теорема 3 . Длину биссектрисы треугольника (рис.6) можно найти по формуле:

Доказательство . Рассмотрим рисунок 6

откуда с помощью Теоремы 2 получаем:

что и требовалось доказать.

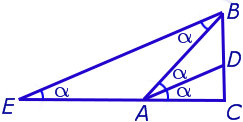
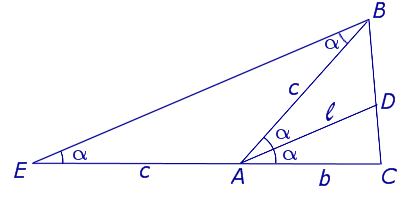
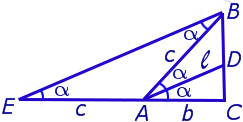
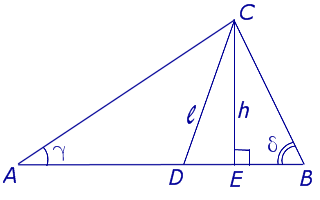
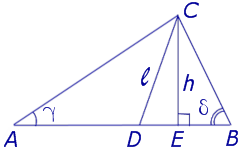
Задача . Из вершины C треугольника ABC (рис.7) проведена биссектриса CD и высота CE .

Доказать, что выполнено равенство:

Решение . Поскольку CD – биссектриса угла ACB , то

Поскольку CE – высота, то

что и требовалось доказать.

Из решения этой задачи вытекает простое следствие.

Следствие . Длины биссектрисы CD и высоты CE связаны следующей формулой:

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Биссектриса — это луч разрезающий угол пополам, а также отрезок в треугольнике обладающий рядом свойств

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком термине, как БИССЕКТРИСА.

Это понятие широко применяется в геометрии. И каждый школьник в России знакомится с ним уже в 5 классе. А после эта величина часто используется для решения различных задач.

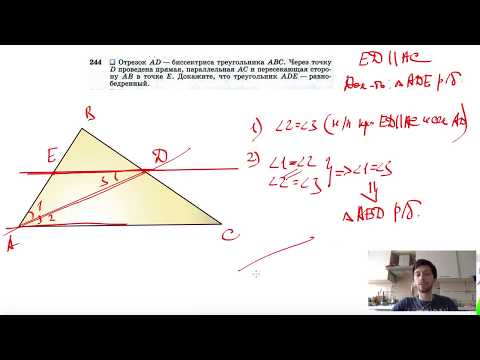
Видео:№244. Отрезок AD — биссектриса треугольника ABC. Через точку D проведена прямая, параллельная АССкачать

Биссектриса — это.

Биссектриса – это луч, который выходит из вершины треугольника и делит ее ровно на две части.

Также под биссектрисой принято понимать и длину отрезка (что это?), который начинается в вершине треугольника, а заканчивается на противоположной от этой вершины стороне.

Есть еще понятие «биссектриса угла», которая является лучом и точно так же делит угол (любой, не обязательно треугольника) пополам:

Само понятие БИССЕКТРИСА пришло к нам из латинского языка. И название это весьма говорящее. Оно состоит из двух слов – «bi» означает «двойное, пара», а «sectio» можно дословно перевести, как «разрезать, поделить».

Вот и получается, что само слово БИССЕКТРИСА – это «разрезание пополам», что собственно и отражается в определении термина, который мы только что привели.

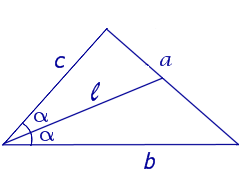
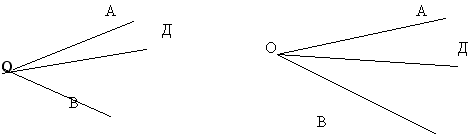
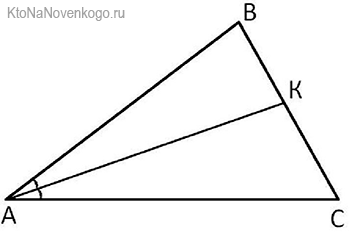
А сейчас задачка на закрепление материала. Посмотрите на эти рисунки и скажите, на каком изображена биссектриса. Подумали? Правильно, на втором.

На первом луч, выходящий из угла АОВ, явно не делит его пополам. На втором это соотношение углов более очевидно, а потому можно предположить, что луч ОД является БИССЕКТРИСОЙ. Хотя, конечно, на сто процентов это утверждать сложно.

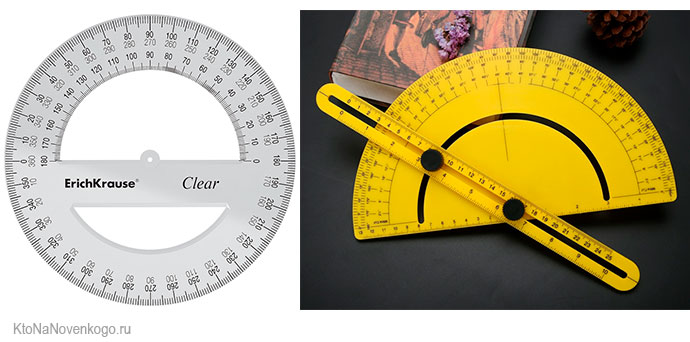
Для более точного определения используют специальные инструменты. Например, транспортир. Это такой инструмент в виде полусферы из металла или пластмассы. Вот как он выглядит:

Хотя есть еще вот такие варианты:

Наверняка у каждого такие были в школе. И пользоваться ими весьма просто. Надо только ровненько совместить основание транспортира (прямоугольная линейка) с основанием треугольника, а после на полусфере отметить значение, которое соответствует размеру угла.

И точно по такой же схеме можно поступить наоборот – имея транспортир, начертить угол необходимого размера. Чаще всего – от 0 до 180 градусов. Но на втором рисунке у нас транспортир, который помогает начертить градусы от 0 до 360.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Количество биссектрис в треугольнике

Но вернемся к нашей главной теме. И ответим на вопрос – сколько БИССЕКТРИС есть в треугольнике?

Ответ в общем-то логичен, и он заложен в самом названии нашей геометрической фигуры. Треугольник – три угла. А соответственно, и биссектрис в нем будет тоже три – по одной на каждую вершину.

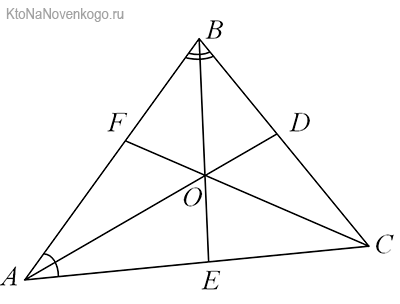
Снова посмотрим на наши рисунки. В данном случае наглядно видно, что у треугольника АВС (именно так в геометрии обозначается эта фигура – по наименованию ее вершин) три БИССЕКТРИСЫ. Это отрезки AD, BE и CF.

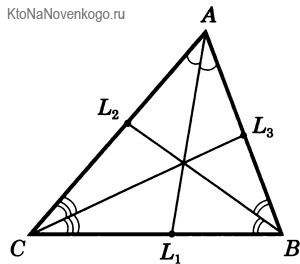
На чертежах БИССЕКТРИСЫ обозначатся следующим образом. Видите одинарные выгнутые черточки между отрезками АС /AL1 и АВ/AL1? Так обозначаются углы. А то, что они оба обозначены одинаковыми черточками, говорит о том, что углы равны. А значит, отрезок AL1 является БИССЕКТРИСОЙ.

То же самое относится и к углам между АВ/DL2 и ВС/BL2. Они обозначены одинаковыми двойными черточками. А значит, отрезок BL2 – биссектриса. А углы АС/CL3 и ВС/CL3 обозначены тройными черточками. Соответственно, это показывает, что отрезок CL3 также является биссектрисой.

Видео:Отрезок KB является биссектрисой треугольника KLM Окружность радиуса 5 проходит через вершину KСкачать

Пересечение биссектрис треугольника

Как можно было заметить по приведенным выше рисункам, у биссектрис треугольника есть одно важное свойство. А именно:

Биссектрисы треугольника всегда пересекаются в одной точке, называемой инцентром!

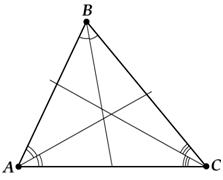
Это правило является аксиомой (что это такое?) и не допускает никаких исключений. Другими словами, вот такого быть не может:

Если вы видите такую картину, то перед вами точно не БИССЕКТРИСЫ. Во всяком случае, минимум один отрезок таковой не является. А может и все три.

А есть еще один интересный факт, связанный с пересечением биссектрис треугольника.

Центр пересечения биссектрис в треугольнике является центром окружности, который списан в эту фигуру.

Это свойство биссектрис на самом деле не только выглядит интересно на чертежах. Оно часто помогает в решение сложных задач.

Видео:Биссектрисы треугольника.Скачать

Свойство основания биссектрисы

У каждой БИССЕКТРИСЫ есть основание. Так называют точку пересечения со стороной треугольника. Например, в нашем случае это будет точка К.

И с этим основанием связана одна весьма интересная теорема. Она гласит, что

Биссектриса треугольника делит противоположную сторону, то есть точкой основания, на два отрезка. И их отношение равно отношению двух прилежащих сторон.

Звучит несколько тяжеловато, но на деле выглядит весьма просто. Отношение отрезков на основании биссектрисы – это ВК/КС. А отношение прилежащих сторон – это АВ/АС. И получается, что в нашем случае теорема выглядит вот так:

Интересно, что для данной теоремы будет справедливо и другое утверждение:

Ну, как часто бывает в математике – это правило работает и в обратном направлении. То есть, если вы знаете длины все сторон и их соотношения равны, то можно сделать вывод, что перед нами БИССЕКТРИСА, А соответственно, будет проще рассчитать размер угла треугольника.

Видео:3 свойства биссектрисы #shortsСкачать

Биссектриса равнобедренного треугольника

Для начала напомним, что такое равнобедренный треугольник.

Это такой треугольник, у которого две стороны абсолютно равны (то есть имеет равные «бедра»).

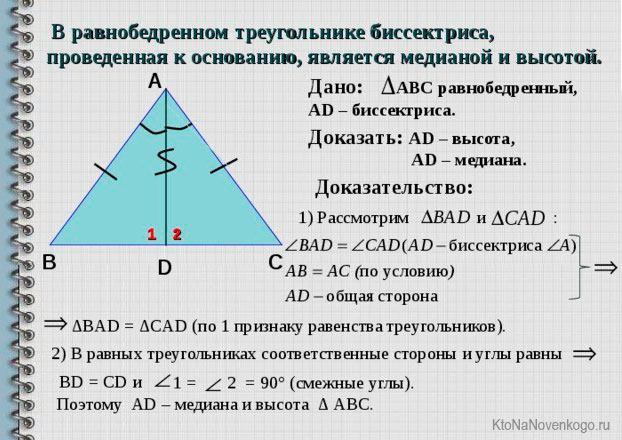
Так вот в таком треугольнике БИССЕКТРИСА имеет весьма интересные свойства.

Она одновременно является еще и медианой (что это?), и высотой.

Эти понятия нам также знакомы по школьному курсу. Но если кто забыл, мы обязательно напомним:

Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.
Медиана – линия, которая выходит из вершины треугольника, и делит противоположную сторону на две ровные части.

А в равностороннем треугольнике или как его еще называют правильном (у которого все стороны и все углы равны) все три биссектрисы являются высотами и медианами. И плюс ко всему, их длины равны.

Вот и все, что нужно знать о таком понятии, как БИССЕКТРИСА. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (3)

«Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.

Медиана – линия, которая выходит из вершины треугольника, и делит противоположную сторону на две ровные части.»

Некорректно, линия бывает разная,а речь здесь идет о прямой, или её порождениях: отрезок и луч.

Математика требует точности. Спасибо.

При ознакомлении с таким теоретическим материалом всегда возникает вопрос, как можно использовать знания о биссектрисе в реальной жизни, за пределами учебного заведения.

Необходимость делать уроки с собственным ребенком в счет не идет. Конечно, такая информация повышает общую эрудицию, но не несет никакой практической нагрузки, а потому надолго не задерживается в памяти.

Никогда не был силен в геометрии, но наука эта очень важна, знаю, потому как не раз приходилось подтягивать свои знания для решения практических задач.