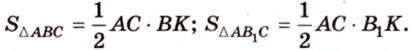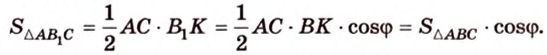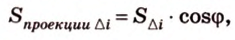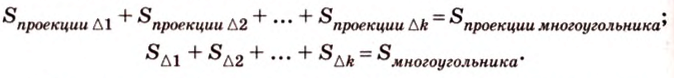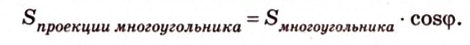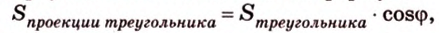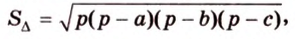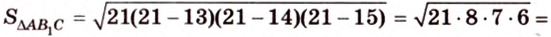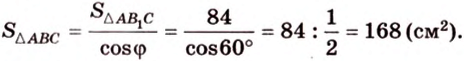Ортогональная проекция прямоугольный треугольник

Ортогональное проецирование:

Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.

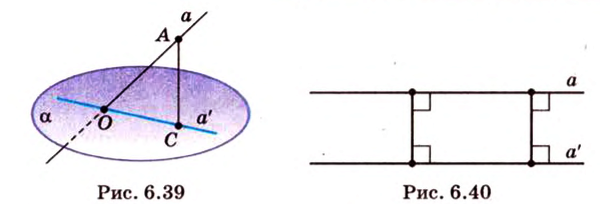
Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой

Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.

Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.

Площадь ортогональной проекции

Теорема 5

Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.

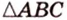
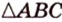
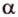
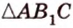
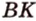
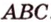
Как пример многоугольника возьмем (рис. 6.41). Проекцией на плоскость является . Проведем высоту треугольника . По теореме
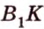
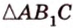
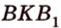
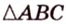
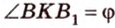
о трех перпендикулярах — высота . Угол — угол между плоскостью и плоскостью проекции. Пусть . Тогда

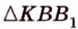
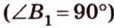
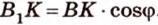
Учитывая, что прямоугольный , имеем:. Поэтому

Итак, . Теорема доказана.

Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство

где 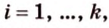поскольку угол между плоскостями этих треугольников и плоскостью их проекций будет один и тот же. Все эти равенства сложим почленно:

Получим в левой части равенства площадь проекции многоугольника, а в правой — площадь самого многоугольника, умноженную на косинус угла между их плоскостями. Отсюда

Т.е. и для этого случая теорема истинна.

Пример:

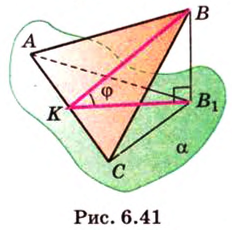
Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.

Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:

где 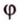— угол между плоскостью треугольника и плоскостью проекции.
По формуле Герона найдем площадь :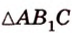

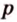
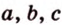
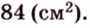
где — полупериметр треугольника, — его стороны.

Тогда

• Декартовы координаты на плоскости
• Декартовы координаты в пространстве
• Геометрические преобразования в геометрии
• Планиметрия — формулы, определение и вычисление
• Параллельность прямых и плоскостей
• Перпендикулярность прямой и плоскости
• Взаимное расположение прямых в пространстве, прямой и плоскости
• Перпендикулярность прямых и плоскостей в пространстве

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Ортогональная проекция и ортогональная составляющая. ТемаСкачать

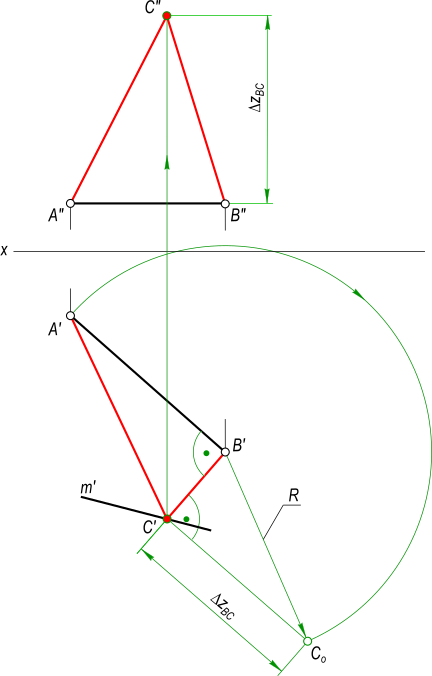
Проекции прямоугольного треугольника

Построить Проекции прямоугольного треугольника ABC, если его катет AB(A`B`, . ) принадежит горизонтальной прямой h(h`, h»), катеты равны между собой, а вершина C принадлежит прямой m(m`, . ) и zC больше zB

AB — один из катетов прямоугольного треугольника, представляет собой прямую уровня — горизонтальную прямую так как A»B» || Ox. На горизонтальную плоскость проекции он проецируется в натуральную величину. Выполняем построение BC: — прямой угол при вершине B проецируется без искажения на горизонтальную плоскость проекции, следовательно здесь можно провести направление для катета BC; — в пересечении направления катета BC с m` получим C`. По способу прямоугольного треугольника определяем Δz = zC-zB: — из центра O описываем дугу радиусом R=|AB|=A`B` до пересечения с направлением перпендикуляра в точке C0; — определяем разницу аппликат катета BC — Δz. Откладываем Δz на фронтальной плоскости проекций от точки B» и по линии проекционной связи находим точку C».

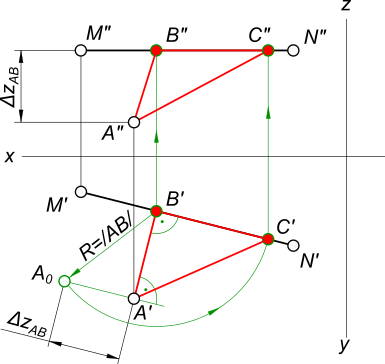
Построить проекции прямоугольного равнобедренного треугольника ABC, катет которого BC лежит на прямой MN. A(60,40,10), M(75,10,30); N(15,25,30).

Так как zM=zN делаем вывод, что отрезок MN — горизонтальная прямая и мы можем опустить из точки A перпендикуляр на него. В пересечении которого с M`N` находим B` и затем по линии проекционной связи B». Находим натуральную величину катета AB способом прямоугольного треугольника:
— через точку A проводим перпендикуляр к AB и на нем откладываем ΔzAB и находим A0 и BA0; — откладываем на отрезке MN катет BC, описывая дугу радиуса R=/AB/ и отмечая точку C` и по линии проекционной связи C»; — вершины A`B`C` и A»B»C» соединяем прямыми линиями, получая проекции искомого треугольника.

Даны проекции равнобедренного прямоугольного треугольника ABC (смотри задачу №1).
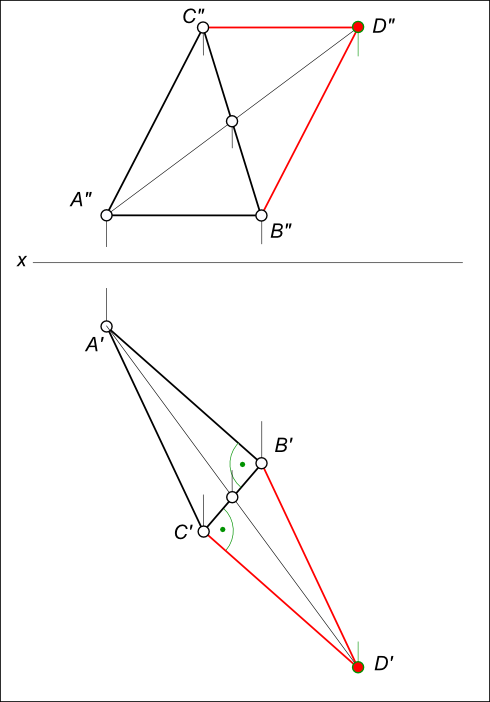
Построить фронтальную и горизонтальную проекции параллелограмма ABCD

Построение параллелограмма заключается: — в проведении BD // AC; — в проведении CD // AB.

Даны проекции равнобедренного прямоугольного треугольника ABC (смотри задачу №1).
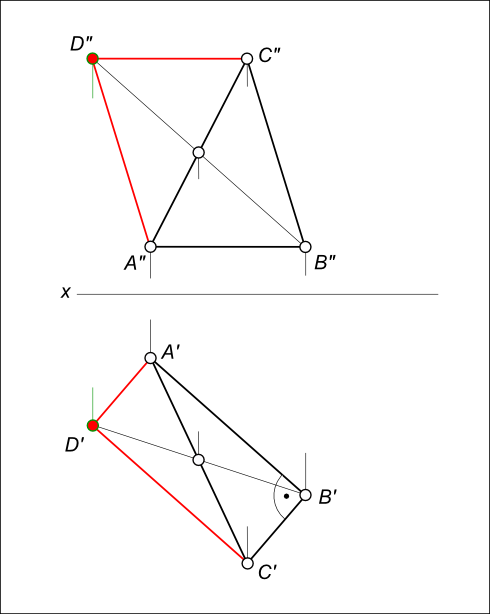
Построить фронтальную и горизонтальную проекции квадрата ABCD

Построение квадрата заключается: — в проведении AD // BC; — в проведении CD // AB.

Видео:Урок 17. Площадь ортогональной проекции Задание 14 ЕГЭ по математике. Стереометрия с нуля.Скачать

Определение натуральной величины отрезка

Если отрезок параллелен плоскости, то он проецируется на неё без искажений. В остальных случаях для нахождения его натуральной величины применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Метод прямоугольного треугольника

Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.

Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник A₀A’B’. Его первый катет A’B’ – это горизонтальная проекция AB. Второй катет A’A₀ равен величине Z_A – Z_B, то есть разности удаления точек A и B от горизонтальной плоскости П₁.

Откладываем A’A₀ = Z_A – Z_B перпендикулярно A’B’. Затем проводим гипотенузу A₀B’ треугольника A₀A’B’. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.

Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Способ параллельного переноса

Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П₁, то длина его проекции E’F’ не изменится, когда она займет новое положение E’₁F’₁ (как это показано на рисунке ниже).

Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.

Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E’₁F’₁ = E’F’ так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E»₁ и F»₁. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости.

Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением. Посмотреть дополнительные примеры и получить более подробную информацию по данной теме можно в этой статье.

Видео:Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Поворот вокруг оси

Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.

Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M’N’ заняла положение M’₁N’₁, параллельное оси X.

По линиям связи находим точку M»₁. При этом исходим из того, что M» в процессе вращения движется параллельно горизонтальной плоскости.

Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N»₁ и M»₁ искомым отрезком. На рисунке он выделен красным цветом.

Более подробную информацию о решении задач методом поворота вокруг оси вы можете получить, ознакомившись со следующим материалом.

📹 Видео

Площадь ортогональной проекцииСкачать

Площадь ортогональной проекции многоугольникаСкачать

Площадь ортогональной проекцииСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

134 Равнобедренный прямоугольный треугольник, проекция которого подобна ему, но меньшей площадиСкачать

Ортогональная проекция точкиСкачать

Ортогональное проектирование Теорема о трех перпендикулярахСкачать

8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Проецирование прямой общего положенияСкачать

#Урок2 Геометрия Прямоугольный треугольник. Проекция.Тригонометрические элементы в прям.треугольникеСкачать

ПОСТРОИТЬ ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА ПО ЗАДАННЫМ УСЛОВИЯМ. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.Скачать

Проекции точки,отрезка,плоскости в ортогональном проецировании.Введение(Часть2.ПРОЕКЦИОННОЕЧЕРЧЕНИЕ)Скачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать