Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
 | ||||
| Внутренняя касательная к двум окружностям | ||||
 | ||||
| Общая хорда двух пересекающихся окружностей | ||||
 | ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Как найти расстояние между центрами | Олимпиадная математикаСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать  Взаимное расположение окружностейВыясним, каким может быть взаимное расположение двух окружностей. Две окружности могут пересекаться, не пересекаться либо касаться друг друга. I. Пересекающиеся окружности имеют две общие точки. Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов: II. Не пересекающиеся окружности не имеет общих точек. Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:
III. Касающиеся окружности имеют одну общую точку — точку касания. При внешнем касании расстояние между центрами окружностей равно сумме их радиусов: При внутреннем касании расстояние между центрами равно разности радиусов: Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0. Видео:Расстояние между центрами. Окружность. Математика 10-11 классы.Скачать  Взаимное расположение прямой и окружности, двух окружностей. ТренажёрТема: Взаимное расположение прямой и окружности, двух окружностей. 1. Даны прямая и окружность радиуса 5. Дано расстояние d от центра окружности до прямой. Определите взаимное расположение прямой и окружности при d = 10, d = 5, d = 0, d = 4. а) окружность и прямая касаются б) окружность и прямая пересекаются в двух точках, причём прямая не проходит через центр окружности в) прямая проходит через центр окружности г) прямая и окружность не имеют общих точек Ответ: при d=10 это г, при d=5 это а, при d=0 это в, при d=4 это б. 2.Хорда АВ окружности удалена от центра окружности на 3. Радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 2. Как расположены эти окружности? Ответ: Окружности касаются внутренним образом. 4. О – центр окружности, А – точка вне её. АО=10, радиус окружности равен 6, а угол ВАО равен 300 . Как расположена прямая АВ относительно окружности? Ответ: пересекает окружность в двух точках. 5. Окружности касаются внутренним образом. Радиус меньшей окружности 3 см, радиус большей окружности — 5 см. Чему равно расстояние между центрами окружностей? а) 8 см; б) 2 см; в) 15 см; г) 3 см. 6. Каково взаимное расположение двух окружностей, если расстояние между центрами равно 10, а радиусы равны 8 и 2? А) внешнее касание; В) внутреннее касание; С) пересекаются; D) не пересекаются. 7. Что можно сказать о взаимном расположении прямой и окружности, если диаметр окружности равен 7,2 см, а расстояние от центра окружности до прямой равно 3,25 см? А) касаются; В) не пересекаются. С) пересекаются; D) нет правильного ответа. 8. Даны окружность с центром О и точка А. Где находится точка А, если радиус окружности равен 7 см, а длина отрезка ОА равна 4 см? А) внутри окружности; В) на окружности. С) вне окружности; D) нет правильного ответа. 9. Радиусы двух концентрических окружностей относятся как 4:5. Найдите их диаметры, если ширина кольца, образованного этими окружностями, равна 7 см. Ответ: 56 см и 70 см. 10. Указать количество общих точек прямой и окружности, если: а) расстояние от прямой до центра окружности — 6 см, а радиус окружности — 7 см; б) расстояние от прямой до центра окружности — 7 см, а радиус окружности — 6 см; в) расстояние от прямой до центра окружности — 8 см, а радиус окружности — 8 см. Ответ: а – 2, б – 0, в — 1. 11. Каково взаимное расположения окружностей если расстояние между центрами d и R1, R2 их радиусы: а) d = 1дм, R1 = 0,8дм, R2 = 0,2дм; б) d = 40см, R1 = 110см, R2 = 70см; в) d = 12см, R1 = 5см, R2 = 3см; г) d = 15дм, R1 = 10дм, R2 = 60 см. Ответ: а – касаются внешним образом, б – касаются внутренним образом, в – вне друг друга, г – пересекаются. 12. Найти длины двух отрезков хорды, на которые разделяет ее диаметр окружности, если длина хорды — 16 см, а диаметр ей перпендикулярен. Ответ: 8см и 8 см. 13. а) Постройте две окружности радиусами 2 см и 4 см, расстояние между центрами которых равно нулю. б) Начертите две окружности разных радиусов (3 см и 2 см), чтобы они касались. Отметьте отрезком расстояние между их центрами. Рассмотрите возможные варианты. в) Постройте окружность с радиусом равным 3 см и прямую расположенную на расстоянии 4 см от центра окружности. г) Постройте окружность с радиусом равным 4 см и прямую расположенную на расстоянии 2 см от центра окружности. 14. В угол С величиной 830 вписана окружность, которая касается сторон угла в точках А и В, точка О – центр окружности. Найдите угол АОВ. Ответ дайте в градусах. Ответ: 970 . 15. На окружности по разные стороны от диаметра АВ взяты точки М и N. Известно, что угол NBA =360 . Найдите угол NMB. Ответ дайте в градусах. Ответ: 540 . 16. Точка О – центр окружности, на которой лежат точки А, В и С. Известно, что угол АВС=750 и угол ОАВ=430 . Найдите угол ВСО. Ответ дайте в градусах. Ответ:320 . 17. В окружности с центром в точке О отрезки АС и ВD – диаметры. Угол АОD равен 1480 . Найдите угол АСВ. Ответ дайте в градусах. 18. На окружности с центром в точке О отмечены точки А и В так, что угол АОВ=660 . Найдите длину большей дуги АВ. Ответ:2940 . 19. На рисунке изображено колесо с пятью спицами. А если бы их было 15, то какой угол был бы между спицами? Ответ: 240 . 20. Найдите угол, который образуют минутная и часовая стрелки часов в 16:00. Ответ дайте в градусах. 21. Через точку А, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке К. Другая прямая пересекает окружность в точках В и С, причём АВ=3, АС=12. Найдите АК. Ответ: 6. 22. Четырёхугольник ABCD описан около окружности, АВ=7, ВС=10, CD=14. Найдите AD. 23. Хорды АС и BD окружности пересекаются в точке Р. ВР=15, СР=6, DP=10. Найдите АР. Ответ: 25. 24. Четырёхугольник ABCD вписан в окружность. Прямые АВ и CD пересекаются в точке К. DK=12, BK=8, BC=6. Найдите AD. Ответ: 9. 25. Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите АС, если диаметр окружности равен 6 , а АВ=4. Ответ: 8. 26. Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АК=14, а сторона АС в 2 раза больше стороны ВС. Ответ: 7. 27. В трапеции АВСD боковая сторона АВ перпендикулярна основанию ВС. Окружность проходит через точки С и D и касается прямой АВ в точке Е. Найдите расстояние от точки Е до прямой СD, если AD=14, BC=12. Ответ 2 📽️ ВидеоУрок 47. Взаимное расположение окружностей (8 класс)Скачать  9 класс, 8 урок, Взаимное расположение двух окружностейСкачать  Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать  Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать  Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать  Взаимное расположение окружностей. 7 класс.Скачать  Найти расстояние между центрами описанной и вписанной окружностей в прямоугольном треугольникеСкачать 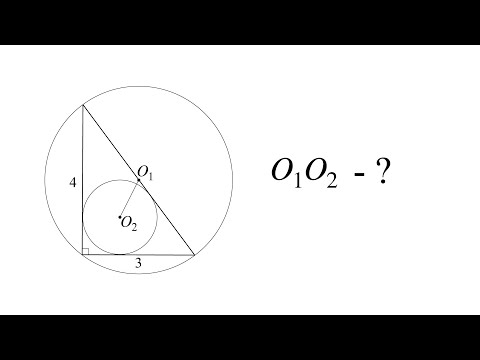 М1152. Расстояние между центрами вписанной и описанной окружностейСкачать 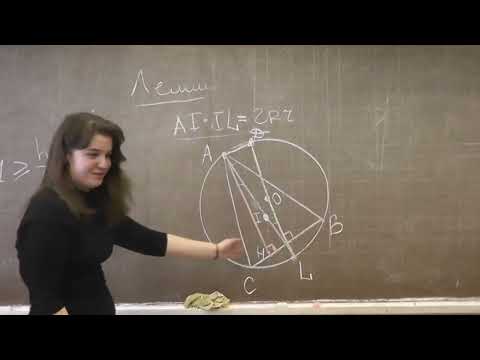 Геометрия 16-02. Взаимное расположение двух и более окружностей. Задача 2Скачать  Взаимное расположение окружностей. Практическая часть. 7 класс.Скачать  8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать  ЕГЭ задание 16 Взаимное расположение окружностейСкачать 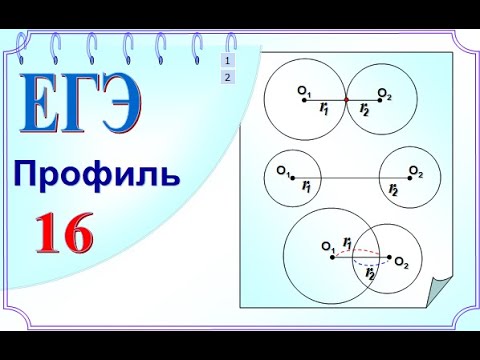 Взаимное расположение прямых в пространстве. 10 класс.Скачать  70. Взаимное расположение прямой и окружностиСкачать  Взаимное расположение окружностей. Окружности не имеют общих точек.Скачать  |




























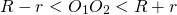


 Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов:
Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов: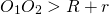 R + r]» title=»Rendered by QuickLaTeX.com»/>
R + r]» title=»Rendered by QuickLaTeX.com»/>
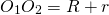

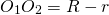


 . Найдите АВ, если диаметр окружности равен 12. 1)10 2)11 3) 12 4) 13.
. Найдите АВ, если диаметр окружности равен 12. 1)10 2)11 3) 12 4) 13.











 .
.