Приведенные выше примеры и теоремы показывают, что установить равномощность различных множеств далеко не просто. В этом параграфе мы рассмотрим примеры построения биекции между различными множествами. Будут приведены примеры доказательств равномощности ряда множеств.
Пример 1. Установить биекцию между отрезком [0, 1] и отрезком [а, в].
Решение. Легко устанавливается биективность линейного отображения x = (в – a)t + a отрезка [0, 1] на отрезок [а, в].
Пример 2. Установить биекцию между интервалом (0, 1) и интервалом (–¥, +¥).
Решение. Легко устанавливается биективность отображения x= ctg(pt) интервала (0, 1) на интервал (–¥, +¥).
Задача. Рассмотреть основные элементарные функции и найти промежутки, на которых они являются биективным отображением.
Пример 3. Построить биекцию между отрезком [0, 1] и интервалом (0, 1).
Решение. Решение этой задачи основано на несчетности рассматриваемых множеств и теореме 4 из параграфа 6. Идея решения состоит в том, что из интервала (0, 1) выделяют некоторое счетное множество А. Затем к нему добавляют две точки и . Вновь полученное множество (обозначим его В Ì [0, 1]), также является счетным. Следовательно, множества А и В равномощны и существует биекция f, отображающая B на A. Построим теперь биекцию отрезка [0, 1] на интервал (0, 1) следующим образом:
Пример 4. Построить биекцию между окружностью единичного радиуса и отрезком [0, 1].
Схема решения. Легко устанавливается биекция между точкой окружности и углом, соответствующим этой точке. Этим получается биекция окружности и полуотрезка [0, 2p). Затем по схеме примера 3 строится биекция полуотрезка [0, 2p) на отрезок [0, 1].
Пример 5. Доказать, что множество всех окружностей на плоскости, радиусы которых рациональные числа и координаты центра которых — рациональные числа, есть счетное множество.
Решение. Нетрудно видеть, что каждый элемент рассматриваемого множества может быть отождествлен с тройкой чисел (х, у, r), где (х, у) — координаты центра окружности, а r — ее радиус. Этим между множеством указанных окружностей и множеством Q´Q´Q устанавливается биекция. Но произведение счетных множеств счетно (см. задачу в 6 параграфе) и, следовательно, наше множество также счетно.
Пример 6. Доказать, что множество точек разрыва монотонной функции, заданной на отрезке [а, в], конечно или счетно.
Видео:Илья Мещерин: Мощности МножествСкачать

Решение задач
1) Можно ли на плоскости построить континуум попарно непересекающихся окружностей?
Возьмем окружность произвольного радиуса a и все концентрические с ней окружности внутри её (окружности эти пересекаться не будут). Каждой окружности поставим в соответствие длину ей радиуса. Радиус может иметь любую длину от 0 до а. Таким образом, множество таких радиусов равномощно отрезку [0, а], т.е. имеет мощность с. А значит и множество концентрических окружностей имеет мощность с. А значит, на плоскости можно построить континуум попарно непересекающихся окружностей.
2) Можно ли написать на доске континуум попарно непересекающихся букв (размеры букв могут быть произвольными) а) Г; б) N; в) А?
- а) Дополним букву Г до прямоугольника и проведем его диагональ из левого верхнего угла (обозначим длину диагонали за a). Зафиксируем правый нижний угол и будем уменьшать диагональ (стороны, образующие букву Г, одного прямоугольника не будут пересекаться со сторонами другого прямоугольника). Каждому прямоугольнику поставим в соответствие длину его диагонали. Длина диагонали может иметь любое вещественное значение от 0 до а. Т.о., множество таких диагоналей имеет мощность с, а значит и множество таких прямоугольников есть мощность континуума. Следовательно, и множество пар левых боковых и верхних сторон прямоугольников (т.е. букв Г) имеет мощность континуума. Т.о., на доске можно написать континуум попарно непересекающихся букв Г.
- б) Напишем под небольшим наклоном букву N. Эта буква состоит из трех отрезков. Проведем четыре вертикальные параллельные прямые через конец каждого отрезка. Ниже данной N изобразим ещё одну N, заключенную между вертикальными прямыми (стороны букв будут попарно параллельны). Эти две буквы отсекают от вертикальных прямых четыре отрезка (обозначим их за a, b, c, d). Установим биекцию между точками отрезков a и b, b и c, c и d при помощи отрезков параллельных сторонам N (отрезки имеют мощность континуума). Т.о., получаем континуум букв N, не пересекающихся между собой и нарисованных на части плоскости.
- в) В каждом треугольнике буквы А выберем точку с рациональными координатами и поставим эту точку в соответствие букве, внутри которой она находится. Т.к. множество рациональных чисел счетно, то и множество пар рациональных чисел счетно (по шестому свойству счетных множеств), т.е. счетно множество точек с рациональными координатами. Поскольку буквы А не пересекаются, точки совпасть не могут. Т.е. на доске можно написать не больше чем счетное «количество» букв А.
- 3) Можно ли построить на плоскости континуум попарно непересекающихся восьмерок?
Поскольку множество рациональных чисел счетно, то и множество точек с рациональными координатами счетно, а, значит, счетно и множество пар точек с рациональными координатами. Выберем в каждом кругу восьмерки по точке с рациональными координатами, и поставим эту пару ей в соответствие. Поскольку восьмерки не пересекаются, каждая пара может встретиться не больше одного раза. Т.о., на доске можно изобразить не больше чем счетное количество восьмерок.
Видео:Такие разные бесконечности. Счётные и несчётные множества | матан #005 | Борис Трушин !Скачать

Счетные множества. Мощность континуума
Эквивалентные множества
1. Установить взаимно–однозначное соответствие между множеством всех натуральных чисел и множеством натуральных чисел, кратных 5.


2. Установить биекцию полуокружности и ее диаметра.
 |

 |



Пусть 
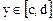

5. Найти взаимно–однозначное отображение интервала 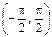
Пусть 


6. (Отель Гилберта). Где-то в далеком космосе есть гостиница с бесконечным числом одноместных номеров, причем все они заселены. В гостиницу приехал человек и попросил поселить его в отдельный номер. Администратор сумел удовлетворить его просьбу, не выселив при этом ни одного постояльца. Как ему удалось это сделать?
Занумеруем номера числами 1, 2, 3, …, n , … Переселим постояльца из 1-го номера во 2-й, из 2-го в 3-й, …, из n-го – в (n+1)-й и т.д. Таким образом, мы освободим 1-й номер, в который и поселим нового постояльца.
7. Найти взаимно–однозначное отображение отрезка 

 |
Так как на первом промежутке точек как бы на одну «больше», то нужно куда-то убрать «лишнюю» точку.
Возьмем на каждом из промежутков произвольную последовательность 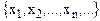

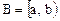
точку x3 из В, …, точке xn из А – точку xn+1 из В и т.д. Таким образом, в В освободится точка x1, которую мы и поставим в соответствие точке b из множества А. Остальные точки в множествах А и В одинаковые, следовательно, мы их поставим в соответствие друг другу.
Таким образом, получим взаимно-однозначное соответствие между А и В.
8. Доказать, что все конечные промежутки числовой прямой эквивалентны.
Как уже показано в № 4, все одноименные промежутки (то есть все сегменты, все интервалы и т.д.) эквивалентны между собой, а в предыдущем примере мы показали, что и разноименные промежутки тоже эквивалентны, что и требовалось доказать.
9. Доказать, что любой промежуток числовой прямой эквивалентен всей числовой прямой.
10. Существует ли непрерывная функция, отображающая взаимно–однозначно отрезок 
Нет, так как, если функция непрерывна на сегменте, то множеством ее значений тоже является сегмент.
Домашние примеры
11. Найти взаимно–однозначное отображение отрезка 



12. Найти взаимно–однозначное отображение полусегмента 

С помощью функции y = tgx.
13. Существует ли непрерывная функция, отображающая взаимно–однозначно отрезок 

14. Существует ли непрерывная функция, отображающая взаимно–однозначно отрезок 
В 13 и 14 ответ «нет» (см. задачу 10).
15. Установить взаимно–однозначное соответствие между окружностью и прямой.
 |
Точке О соответствует бесконечно удаленная точка числовой прямой.
Счетные множества. Мощность континуума
1. Какова мощность множества 
Это множество является объединением двух последовательностей. Поскольку последовательность – это счетное множество, то и множество А счетно.
2. Какова мощность множества точек на плоскости, у которых обе координаты рациональны?.
Множество точек на плоскости 

3. Какова мощность множества всех треугольников на плоскости, вершины которых имеют рациональные координаты?
Это множество счетно (см. задачу 2).
4. Доказать, что множество всех окружностей на плоскости, радиусы которых рациональны и координаты центра – рациональные числа, счетно.
5. Доказать, что если расстояние между любыми двумя точками множества Е на прямой больше 1, то множество Е не более, чем счетно.
Окружим каждую точку множества окрестностью, длиной 1, тогда эти окрестности не будут пересекаться. В каждой окрестности выберем рациональное число. Получим некоторое множество А рациональных чисел, которое находится во взаимно-однозначном соответствии с множеством Е. Так как множество А – часть множества Q, то оно не более чем счетно, следовательно, множество Е тоже не более чем счетно.
6. Доказать эквивалентность сегмента 

Так как 



7. На прямой задано множество попарно не пересекающихся отрезков. Что можно сказать о мощности этого множества?
Это множество не более чем счетно (см. задачу 5).
8. Доказать, что множество точек разрыва монотонной функции, заданной на всей числовой прямой, конечно или счетно.

Поставим каждой точке разрыва, например, х1 в соответствие сегмент 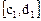
📹 Видео
МОЩНОСТЬ МНОЖЕСТВА / СЧЕТНЫЕ МНОЖЕСТВАСкачать

Мощность континуума | Теория множествСкачать

Множества и операции над нимиСкачать

Мощность множества. Эквивалентные множестваСкачать

Видеоурок "Мощность множеств"Скачать

Теория множеств: логика, формализм и кризисСкачать

Множество. Элементы множества. 5 класс.Скачать

Яворская Т.Л. - Понятийный аппарат математики - 8. Мощность множествСкачать

A.2.10 Мощность и граница множества (переснято)Скачать

9 класс, 2 урок, Множества и операции над нимиСкачать

Что такое Булеан? Мощность булеанаСкачать

Математика для всех. Алексей Савватеев. Лекция 3.7. Множество всех подмножеств. Теорема КантораСкачать

Теория множеств. Мощность множества. Математика за минуту #shortsСкачать

Задачи на множества. Мощность множеств. Математика 6 класс. Теория множествСкачать

Множества — Принципы математического мышления — уровень 5 из 5Скачать

Математика для всех. Алексей Савватеев. Лекция 3.6. Конечные и бесконечные множестваСкачать

Множества. Операции над множествами. 10 класс алгебраСкачать

Операции над множествамиСкачать