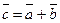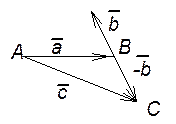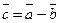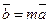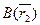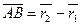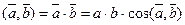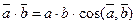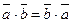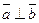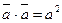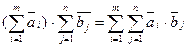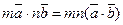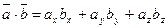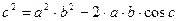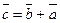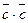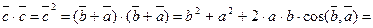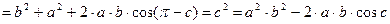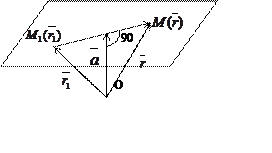Какому условию должны удовлетворять векторы

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).

рис. 1

Видео:Угол между векторами. 9 класс.Скачать

Условия коллинеарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

Доказательство третего условия коллинеарности

Пусть есть два коллинеарные вектора a = < a_x ; a_y ; a_z > и b = < na_x ; na_y ; na_z >. Найдем их векторное произведение

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Примеры задач на коллинеарность векторов

Примеры задач на коллинеарность векторов на плоскости

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:

Для этого найдем ненулевой компонент вектора a в данном случае это a_y . Если вектора колинеарны то

Найдем значение n a :

Так как b = n a , то вектора a и b коллинеарны.

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности

Решим это уравнение:

Ответ: вектора a и b коллинеарны при n = 6.

Примеры задач на коллинеарность векторов в пространстве

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:

Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12

Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12

Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:

Для этого найдем ненулевой компонент вектора a в данном случае это a_y . Если вектора колинеарны то

Найдем значение n a :

Так как b = n a , то вектора a и b коллинеарны.

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности

Из этого соотношения получим два уравнения:

Решим эти уравнения:

Ответ: вектора a и b коллинеарны при n = 6 и m = 4.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Векторная алгебра. Векторно-скалярное произведение. Двойное векторное произведение

Страницы работы

Фрагмент текста работы

Вектором называется величина, характеризующая помимо измеряющего в определённых единицах числа, ещё своим направлением в пространстве.

Численное значение вектора называется величиной, модулем или длиной вектора.

Для численного задания вектора нужно указать три числа. Это либо длина вектора и направление, которое задается двумя числами, либо три скалярных величины.

Поэтому равенство трёх векторов сводится к равенству попарно трёх чисел, эти векторы определяющих.

Вывод: Одно векторное равенство равно трём скалярным равенствам.

Различают векторы трёх видов: свободные передвижные и определенные векторы.

Точку приложения свободных векторов можно выбирать произвольно.

У передвижных векторов точку приложения вектора можно перемещать вдоль самого вектора.

У определённых векторов точка приложения вектора должна быть зафиксирована.

Изучение передвижных и определённых векторов сводится к изучению свободных векторов, поэтому достаточно ограничиться рассмотрением только свободных векторов.

1. Сумма векторов. Чтобы получить вектор , представляющий геометрическую сумму двух векторов и , надо от произвольной точки А пространства отложить вектор , к концу его приложить начало вектора , тогда по величине и направлению представляет вектор .

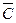
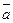
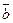
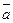
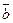
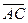
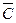
Рис. 1. Сложение векторов.

2. При сложении нескольких векторов каждый последующий вектор складывается с суммой предыдущих векторов.

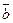
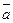
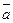
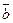
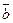
Для вычитания вектора из вектора необходимо прибавить к вектору вектор —, противоположный вектору .

Рис. 2. Вычитание векторов.

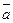
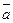
3. Умножение вектора на целое положительное число. Умножить вектор на целое положительное число m – значит сложить между собой m векторов равных .

4. Два параллельные между собой вектора называются коллинеарными.

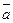
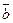
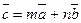
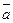
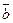
5. Если векторы и не коллинеарны, то вектор параллелен плоскости, определяемый векторами и .

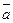
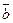
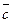
В этом случае говорят, что векторы , , , компланарны, т.е. параллельны одной плоскости.

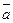
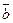
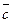
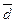
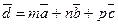
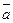
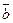
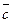
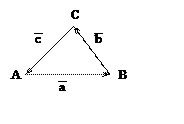
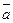
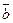
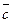
6. Если три вектора , и не компланарны, то всяких вектор может быть представлен в форме , т.е. разложен на три составляющие параллельные соответственно векторам , и .

Задача 1. Какому условию должны удовлетворять три вектора , и , чтобы из них можно было образовать треугольник.

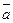
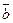
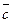
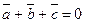
Из чертежа видно, что сумма векторов , и должна быть равна нулю. .

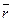
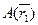
Задача 2. Найти радиус-вектор середины С отрезка АВ, зная точки ,

Положение какой-либо точки пространства может быть определено вектором, соединяющим рассматриваемую точку с начальной произвольно выбранной точкой (началом координат).

Будем называть вектор , имеющий начало в точке О, а конец в точке Р радиус-вектором точки Р относительно точки О и будем его обозначать как . Про точку Р будем говорить, что дана точка .

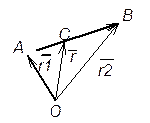
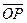
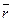
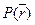
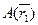
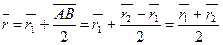
Имеем вектор, соединяющий точки и

.

Задача 3. Доказать, что если диагонали четырехугольника делят друг друга пополам, то четырех угольник есть параллелограмм.

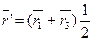
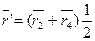
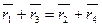
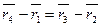
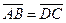
Решение ; ; Отсюда или , т.е. .

Это означает, что сторона АВ = DC и АВ || DC. Т.е. четырехугольник — параллелограмм.

Скалярное или внутреннее произведение двух векторов.

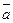
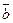
Скалярным или внутренним произведением двух векторов и называется произведение длин обоих векторов, умноженное на косинус угла между обоими векторами.

В результате получаем скаляр.

Скалярное произведение равно произведению длины одного из векторов на проекцию другого вектора на направление первого.

Важнейшие свойства скалярного произведения.

1.

2.

3. , если или или

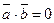
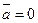
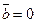
4. , если a и b коллинеарны, в частности

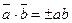
5.

6.

7.

Задача 4. Дан треугольник ΔАВС.

Вывести основную формулу геометрии

Из рисунка имеем

Умножим скалярно

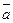
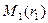
Задача 5. Найти уравнение плоскости, перпендикулярной к заданному вектору и проходящий через точку .

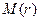
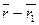
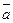
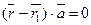
Возьмем любую точку плоскости, тогда вектор лежит в плоскости, а вектор перпендикулярен плоскости. Уравнение представляет уравнение некоторой плоскости О.

Векторное или внешнее произведение двух векторов.

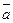
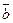
Векторным или внешним произведением двух векторов и называется вектор

Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Ортогональные векторы и условие ортогональности

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Ортогональные векторы: определение и условие

Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .

Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a ¯ = и b ¯ = записывают следующим образом:

a ¯ × b ¯ = a x × b x + a y × b y = 0

Задача 1. Докажем, что векторы a ¯ = и b ¯ = ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) = 2 — 2 = 0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Задача 2. Докажем, что векторы a ¯ = и b ¯ = ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 3 × 7 + ( — 1 ) × 5 = 21 — 5 = 16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Задача 3. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = — 4 n = — 2

Ответ: векторы являются ортогональными при значении n = 2 .

Видео:Скалярное произведение векторов. 9 класс.Скачать

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a ¯ = и b ¯ = условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .

Задача 4. Докажем, что векторы a ¯ = и b ¯ = являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) + 0 × 10 = 2 — 2 = 0

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( — 8 ) = 2 n + 4 — 8 = 2 n — 4 2 n — 4 = 0 2 n = 4 n = 2

Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .

🔍 Видео

Коллинеарность векторовСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Коллинеарные векторы.Скачать

Условие перпендикулярности векторов. 11 класс.Скачать

10 класс, 43 урок, Компланарные векторыСкачать

Как разложить вектор по базису - bezbotvyСкачать

Скалярное произведение векторовСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Аналитическая геометрия, 3 урок, Векторное произведениеСкачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

2 42 Ортогональность векторовСкачать

Векторы для чайников (что потребуется знать при решении физических задач)Скачать

Векторное произведение векторовСкачать