Какие элементы окружности вы знаете

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Видео:Урок 7. Окружность, круг и их элементы. ОГЭ. Вебинар |МатематикаСкачать

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Видео:7 класс, 21 урок, ОкружностьСкачать

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Видео:Окружность и круг, 6 классСкачать

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Видео:Окружность. Круг. 5 класс.Скачать

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Видео:Окружность. 7 класс.Скачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Видео:Круг. Окружность (центр, радиус, диаметр)Скачать

Элементы окружности

Окружность — множество всех точек плоскости, удаленных на заданное расстояние (равное радиусу) от заданной точки этой же плоскости (центра окружности).

Радиусы — отрезки, соединяющие точки окружности с центром. Все радиусы данной окружности равны.

Хорда — отрезок, соединяющий любые две точки окружности.

Диаметр — хорда, проходящая через центр окружности. Диаметр, делящий хорду пополам, перпендикулярен этой хорде.

Центральный угол — угол, образованный двумя радиусами. Центральный угол измеряется дугой, на которую опирается.

Вписанный угол — угол, вершина которого лежит на окружности, а стороны являются ее хордами.

Касательная — прямая, проходящая через точку окружности, перпендикулярно ее радиусу. Касательная имеет с окружностью только одну общую точку.

Длина окружности: 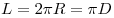, — радиус окружности, — диаметр.

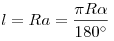
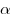
Длина дуги окружности: , — радианная мера дуги, — градусная мера.

Круг — часть плоскости, ограниченная окружностью.

Площадь круга: .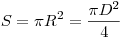

Сектор — часть круга, ограниченная двумя радиусами и дугой окружности.

Площадь сектора: .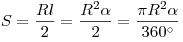

Сегмент – часть круга, ограниченная хордой и дугой.

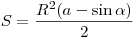
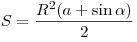
Площадь сегмента: (или , если центр круга лежит внутри сегмента).

Видео:РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Окружность. Основные понятия.

Окружностью называется фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки (центра).

Часть, плоскости, ограниченная окружностью, называется кругом.

Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом.

Отрезок, соединяющий две точки окружности, называется её хордой.

Хорда, проходящая через центр окружности, называется диаметром.

D = 2R

Угол с вершиной в центре окружности называется центральным углом.

Часть окружности называется дугой.

Градусная мера дуги равна градусной мере центрального угла.

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

Вписанный в окружность угол равен половине градусной меры дуги

и, соответственно, половине центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу, равны между собой.

Вписанные углы ACB, ADB, AEB равны, потому что опираются на одну дугу АВ.

Вписанный угол, опирающийся на диаметр, — прямой.

И обратно, если вписанный угол — прямой, то он опирается на диаметр.

OH — расстояние от центра до хорды.

Треугольники AOH и BOH равны.

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности. Их общая точка называется точкой касания прямой и окружности.

Касательная перпендикулярна к радиусу, проведенному в точку касания.

Точка касания двух касающихся окружностей принадлежит прямой, которая проходит через центры этих окружностей.

Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.

Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла.

Круговым сегментом называется часть круга, заключённая между дугой окружности и её хордой.

Длина дуги и площадь сектора прямо пропорциональны градусной мере дуги и угла сектора.

Длина дуги так относится к длине окружности, как градусная мера дуги относится к градусной мере окружности.

Площадь сектора так относится к площади круга, как градусная мера угла сектора относится к градусной мере полного угла.

Чтобы найти площадь сегмента нужно соединить концы хорды с центром окружности и рассмотреть получившиеся сектор и треугольник.

Если сегмент меньше полукруга, то его площадь равна площади сектора минус площадь треугольника.

Если сегмент больше полукруга, то его площадь равна площади сектора плюс площадь треугольника.

💡 Видео

Длина окружности. Математика 6 класс.Скачать

Окружность, диаметр, хорда геометрия 7 классСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Быстро и легко определяем центр любой окружностиСкачать

Радиус и диаметрСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Задание 16 ОГЭ 2023 математика | Окружность, круг и их элементыСкачать

Длина дуги окружности. 9 класс.Скачать

ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Задание 16 (часть 1) | ОГЭ 2024 Математика | Окружность, круг и их элементыСкачать

	Если две окружности имеют только одну общую точку, то они называются касающимися друг друга в этой точке.
	Отношение длины любой окружности L к ее диаметру D = 2R есть величина постоянная. L/2R = π Число π ≈ 3,1415926535897932384626433832795. — иррациональное и в десятичном виде представляет собой бесконечную непериодическую дробь.
	Одна и та же хорда окружности может быть границей разных сегментов.