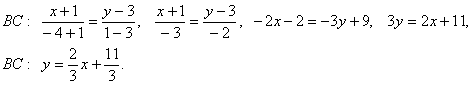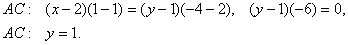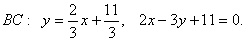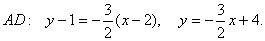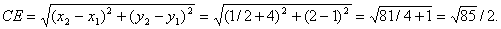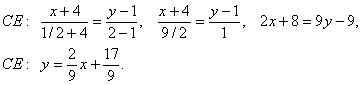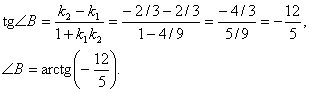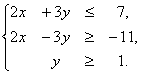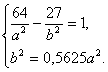Задача 1. Даны вершины треугольника А(-3;-2), В(1;8), С(5;3).
Найти: а) уравнения всех трех его сторон;
б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны;
в) внутренний угол А треугольника в градусах и минусах;
г) длину высоты, опущенной из вершины А;
д) площадь треугольника.
а) Уравнения сторон найдем по формуле прямой, проходящей через две данные точки 
Уравнение стороны АВ: 
, или 
(АВ).
Уравнение стороны АС: 
или 
(АС)
б) Каждая из прямых, уравнения которых только это найдены, разделяет плоскость на две полуплоскости, определяемые соответствующими неравенствами.
Чтобы определить знаки этих неравенств, возьмем координаты какой-нибудь точки заведомо расположенной внутри треугольника АВС (см. рисунок 1). Такой точкой является, например точка N (0;1) подставляя координаты этой точки в уравнения граничных прямых (сторон) в силу того, что точка N не лежит ни на одной сторон, получим следующую систему неравенств. 
определяющих множество внутренних точек треугольника.
Система неравенств 
определяет множество точек, принадлежащих треугольнику АВС, включая его стороны.
в) Внутренний угол треугольника найдем, зная угловые коэффициенты сторон АВ и АС, образующих этот угол, по формуле 
.
Угловые коэффициенты прямых выложим по формуле 
.
Получим 
; 
.
Тогда 
. Угол определяем с помощью таблицы тангенсов или калькулятора
г) Длину высоты AD ^ BC (рис. 1) найдем как расстояние от данной точки А(-3;-2) до данной прямой ВС: 5х + 4у – 37 = 0 по формуле
, где А, В, С – коэффициенты прямой, 
— координаты данной точки.
Получим 
(мин. ед.)
д) Площадь треугольника можно вычислить несколькими способами.
Вычислить ее через координаты вершин треугольника по формуле 
.
Получим 
.
Итак, площадь треугольника SABC = 30 кв. ед.
Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать
Как задать треугольник системой неравенств
уравнение и длину высоты А D ; уравнение и длину медианы СЕ; внутренний угол В; систему линейных неравенств, определяющую треугольник. Сделать чертеж.
Y
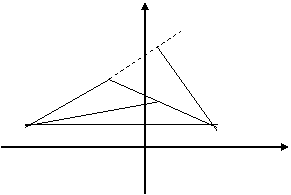
1. Составим уравнения всех сторон треугольника, используя уравнение прямой, проходящей через две данные точки.
.
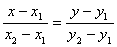
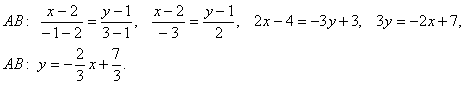
Так как точки А и С имеют одинаковую ординату, используем данное уравнение в преобразованном виде:
.
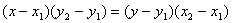
2. Найдем длину высоты А D . Используем формулу расстояния от точки до прямой:
.
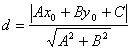
Приведем уравнение ВС к общему уравнению прямой.
.
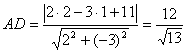
3. Составим уравнение высоты А D . Она проходит через точку А(2,1) и перпендикулярна прямой ВС, k BC =2/3. Из условия перпендикулярности k AD =-1/ k BC =-3/2. Воспользуемся уравнением прямой, проходящей через данную точку в данном направлении:
.
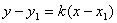
4. Для нахождения длины и уравнения медианы СЕ найдем координаты точки Е как середины отрезка АВ.
Точка Е (1 /2,2).
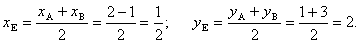
5. Найдем внутренний угол В. Он отсчитывается в положительном направлении от прямой ВС к прямой АВ. k BC =2/3, k AB =-2/3.
6. Составим систему линейных неравенств, определяющую треугольник. Запишем уравнения сторон в виде
AB : 2 x + 3 y = 7 ,
BC : 2 x — 3 y =- 11 ,
Подставим точку с координатами (-1, 2), лежащую внутри треугольника, в левые части равенств.
2 x — 3 y =- 2-6=-8>-11,
Следовательно, система неравенств, описывающая треугольник, имеет вид
Задача 2. Составить каноническое уравнение гиперболы, если известно, что ее эксцентриситет равен 1,25 и гипербола проходит через точку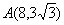 
.
Решение . Каноническое уравнение гиперболы имеет вид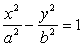 
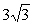
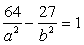
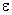
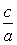
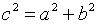
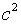
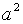
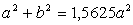
. Так как гипербола проходит через точку А (8; 
), то ее координаты удовлетворяют уравнению гиперболы, т.е. 
. Так, как 
= 1,25, то 
= 1,25, но 
, тогда 
= 1,5625 
или 
.
Итак, получаем систему двух уравнений с двумя неизвестными а и b .
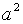
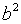
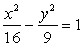
Решая эту систему, находим = 16 и 
= 9, следовательно, каноническое уравнение гиперболы имеет вид 
.
Задача 3. Составить уравнение прямой, проходящей через вершину параболы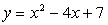 
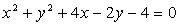
и центр окружности 
.
Решение . Найдем координаты вершины параболы и координаты центра окружности. Для этого выделим полные квадраты по каждой переменной.
Уравнение параболы: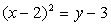 
;
уравнение окружности: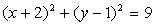 
.
Следовательно, вершина параболы имеет координаты В (2;3), а центр окружности имеет координаты С (-2; 1).
Тогда уравнение искомой прямой составим по формуле
.
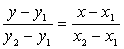
Получим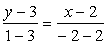 
, или 
.
Видео:Неравенства треугольника. 7 класс.Скачать
Системы неравенств с двумя переменными
п.1. Алгоритм графического решения системы неравенств с двумя переменными
 |
