Как выглядит раз треугольник

Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Определение треугольника

Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.

Посмотрите на треугольник на рисунке.

У него три вершины — , , и три стороны , и . У каждого треугольника есть имя — это имя образовано вершинами треугольника. Наш треугольник зовут ([а-бэ-цэ]). А треугольник на вот этом рисунке

будут звать ([эм-эн-ка]).

По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.

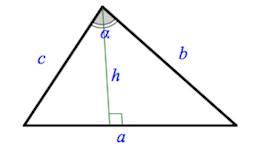
В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.

Видео:Выживший летчик рассказал, что он увидел в Бермудском треугольникеСкачать

Высота треугольника

В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.

Например, в треугольнике , высотой будет отрезок .

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.

В этом треугольнике три высоты , , .

Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.

Видео:Эта Находка в Бермудском Треугольнике Испугала Всех УченыхСкачать

Виды треугольника

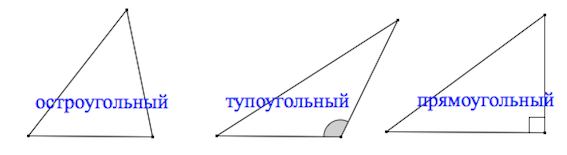
Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.

Виды треугольников по углам

В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный , треугольник бывает остроугольным, тупоугольным или прямоугольным.

Посмотрите на рисунки — перед вами три основных вида треугольника:

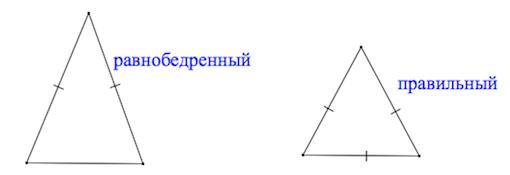
Виды треугольников по сторонам

Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.

На рисунке показаны равносторонний и равнобедренный треугольники.

Видео:ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

Свойства сторон треугольника

Треугольник имеет важные свойства и характеристики.

Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.

Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.

Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:

Например, пусть наш треугольник имеет длины двух сторон , а см. В каком диапазоне будет размер третьей стороны треугольника?

Решение: согласно свойству сторон треугольника, получим:

Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.

Правило существования треугольника

Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.

Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.

Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?

Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Свойство углов в треугольнике

Сумма всех углов в треугольнике равна .

Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна .

Например, пусть известно, что в треугольнике , , , нужно найти .

Так как сумма углов в треугольнике равна , то находим:

.

Ответ: .

Видео:Самые известные тайны Бермудского треугольника: правда или вымысел?Скачать

Элементы композиции

Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.

А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:

Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.

Видео:100 Фактов о Бермудском Треугольнике, о Которых Вы не ЗналиСкачать

Геометрия

План урока:

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Как выглядит треугольник?

В выходной день Глеб с родителями ехали в парк. Мальчик заметил, что вдоль дороги стояла непонятная табличка, увидев которую, отец поехал очень медленно.

«Что это такое?» – поинтересовался ребенок. Папа рассказал, что это дорожный знак, который предупреждает о трудностях на пути. Глебу очень понравился знак, а особенно его форма. Отец продолжил рассказ о знаках: «Форма знака о многом говорит водителю, ведь при плохой видимости автолюбитель видит только форму, а не надпись. Поэтому все предупреждающие знаки – треугольные». «А что такое треугольные?» – не унимался мальчик. Найти ответ на этот и многие другие вопросы папе помог наш сегодняшний урок.

Вначале, давайте разберемся, что же такое треугольник и из чего он состоит.

В повседневной жизни нас окружает масса предметов имеющих треугольную форму. Например:

Часы, воздушный змей, кусочек торта, пиццы, арбуза, салатники, рамки для фотографий, пузырек парфюма – этот список можно продолжать бесконечно. Но что же такое треугольник?

Приведем примеры треугольников:

Исходя из определения, каждый рисунок состоит из трех отрезков. В геометрии такие отрезки называют сторонами треугольника.

Кроме отрезков, составляющей частью фигуры являются три точки, которые принято называть вершинами.

В геометрии, вершины треугольника принято обозначать заглавными буквами латиницы: A,C,D,B.

Начертим треугольник. Вершины, обозначим буквами A,C,D.

Данная геометрическая фигура имеет три вершины A,C,D и три стороны АС, CD, DА.

А как же на письме показать, что данная фигура является треугольником?

Очень интересным является то, что записывать название, можно перечисляя вершины в любом порядке.

Можно записать: ∆NOK, ∆OKN, ∆KNО. Каждый вариант записи обозначает один и тот же треугольник и является верным.

Само название фигуры «Треугольник» предполагает, что в состав должны входить три угла. Так ли это?

Внимательно рассмотрим рисунок:

Действительно, мы видим три угла, которые отмечены дугами: ∠RFP,∠FPR, ∠PRF(мы уже знаем, что буква, обозначающая вершину угла всегда записывается в середине) или∠F, ∠P,∠R.

Видео:Треугольники. 7 класс.Скачать

Виды треугольников

Все геометрические фигуры, имеющие треугольную форму,делятся на группы по двум направлениям:

Давайте рассмотрим, на какие группы делятся треугольники по углам:

Теперь, познакомимся с группами треугольников по сторонам(на рисунках равные стороны принято обозначать одинаковым количеством черточек):

Постарайтесь запомнить все виды треугольников, так как на протяжении всего учебного процесса, вам часто придется сталкиваться с выполнением заданий на данную тему.

Видео:5 Самых Страшных Тайн Бермудского ТреугольникаСкачать

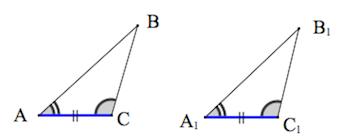
Равенство треугольников

Случаются ситуации, когда точно известно, что два треугольника равны, а что же в таком случае можно сказать про углы и стороны таких треугольников?

Нам дано: ∆ABC = ∆A₁B₁C₁. Равны ли соответствующие стороны и углы данных фигур?

По условию треугольники равны. Значит, применяем рассмотренное правило, которое говорит о том, что все соответствующие элементы фигуры равны между собой.

Если ∆ABC = ∆A₁B₁C_1, то равны соответствующие стороны:

и соответствующие углы равны:

Геометрия интересна тем, что большинство её правил нуждаются в доказательствах. Такие правила называют теоремами.

Вместе с этим, имеются и самостоятельные правила, которые называют аксиомами геометрии.

Сегодня мы рассмотрим первую теорему с названием «Первый признак равенства треугольников», и проведем работу по сбору доказательств для данной теоремы.

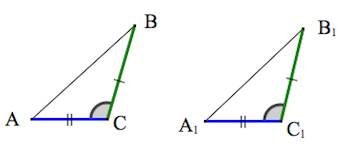
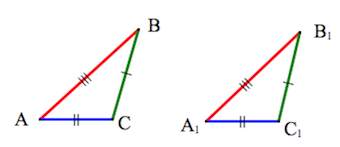
Два треугольника – ∆OMN и ∆KLT. Известно, что две стороны треугольников и угол между ними равны.

Докажем, что ∆OMN=∆KLT.

Доказательство первого признака равенства треугольников:

Из условия нам известно, что соответствующие углы равны ∠M =∠L, следовательно, мы можем выполнить наложение двух треугольников так, чтобы вершина M совпадала с вершиной L.

Тогда, сторона OM наложится на сторону KL, а сторона MN на отрезок LT. По условию нам известно, что отрезки равны OM=KL, MN=LT, значит, при наложении они совпадут. Получается, что при наложении совпадает угол, и две стороны, следовательно, будут совпадать и оставшиеся стороны ON и KT, то есть ON = KT . Если при наложении совмещаются три стороны и одна вершина, значит, совместятся и две другие вершины KO и TN.

Выходит, что при совмещении совпадают все элементы ∆, а такие ∆ называются равными.

Мы доказали, что ∆OMN=∆KLT.

Еще, нам предстоит познакомиться с несколькими понятиями, без которых продолжать изучение геометрии невозможно.

Начертим прямую АВ. Выберем точку не лежащую на данной прямой. Проведем отрезок СК, соединяющий точку С и прямую АВ, таким образом, чтобы при пересечении СК и АВ образовывался прямой угол (90˚) . Изображенный отрезок СК называют перпендикуляром к прямой.

Доказательство будем проводить в два этапа.

Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Медиана, биссектриса, высота

Рассмотрим ∆АВС. Отметим на отрезке АС середину и обозначим её точкой О. Соединим точки В и О отрезком. Полученный отрезок ВО называют медианой.

Любой треугольная фигура имеет три вершины, из каждой можно провести медиану, следовательно, в одной можно провести три медианы.

Биссектриса

Чтобы рассмотреть понятие биссектрисы треугольника, вспомним определение биссектрисы угла:

На рисунке изображен ∆ОВМ. Из угла О проведем биссектрису (луч, делящий угол пополам)и продолжим её до пересечения со стороной ВМ. Место пересечения отметим точкой С. Отрезок ОС делит угол О пополам(∠ВОС =∠СОМ) и пересекается с противолежащей стороной ВМ.

На рисунке изображена фигура РТК. Из вершины Т проведем перпендикуляр к стороне РК, место пересечения перпендикуляра и стороны фигуры отметим точкой А.∠ТАК =∠ТАР=90˚. Перпендикуляр ТА называют высотой ∆РТК.

Изученные сегодня определения и теоремы являются базовыми в изучении геометрии. Поэтому постарайтесь уделить особое внимание материалу сегодняшнего урока.

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Треугольник

Треугольник произвольный

Треугольник – это многоугольник с тремя сторонами (тремя углами).

Виды треугольников :+ показать

Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).

Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).

Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием .

Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.

Свойства

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

3. Сумма углов треугольника равна 180 º .

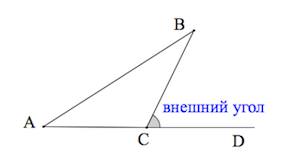
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:

(Внешний угол образуется в результате продолжения одной из сторон треугольника).

5. Любая сторона треугольника меньше суммы двух других сторон.

Признаки равенства треугольников

1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.

2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.

3. Треугольники равны, если у них соответственно равны три стороны.

Биссектриса, высота, медиана

Здесь подробно о биссектрисе, высоте, медиане треугольника.

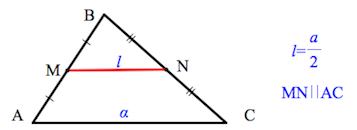
Средняя линия треугольника

Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

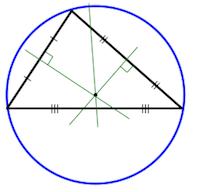
Вписанная окружность

Центр вписанной окружности – точка пересечения биссектрис треугольника.

Описанная окружность

Центр описанной окружности – точка пересечения серединных перпендикуляров.

Соотношение сторон в произвольном треугольнике

Теорема косинусов:

Теорема синусов:

Площадь треугольника

Через сторону и высоту

Через две стороны и угол между ними

Через радиус описанной окружности

Через радиус вписанной окружности

, где – полупериметр

, где – полупериметр

Смотрите также площадь треугольника здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉

Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!

В разделе свойства:

Да, не хватало значка «» у А. Спасибо! 😉

Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.

Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение Откуда Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда

спасибо я так и думал а то не могу решить и всё
СПАСИБО!

Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3

Очевидно,
Примите за .
Примените к треугольнику теорему косинусов:

Найдете , далее можно найти угол и из треугольника найти

Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно

📺 Видео

Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

7 класс, 14 урок, ТреугольникСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Места, Которые Загадочнее Бермудского ТреугольникаСкачать

Я оплачу Все, что ты вместишь в этот ТреугольникСкачать

Краткая история Бермудского треугольникаСкачать

ВСЕ по 100 руб с WILDBERRIES!💞 Товары как в Pinterest, Косметика, Вкусняшки, Аксессуары, КанцелярияСкачать

Бермудский Треугольник - Загадка раскрыта!Скачать