| Название | Учебное пособие Набережные Челны 2003 г |
| Анкор | 1_Вычисления в Excel.doc |
| Дата | 23.09.2017 |
| Размер | 7.26 Mb. |
| Формат файла |  |
| Имя файла | 1_Вычисления в Excel.doc |
| Тип | Учебное пособие #8938 |
| страница | 10 из 16 |
| Подборка по базе: Учебное пособие по речевой коммуникации в профсфере 2018 (1).doc, Экономическая теория. Часть 2. Макроэкономика — пособие (1) (1)., методическое пособие_наращивание волос.docx, Стандартизация, подтв. соответствия Методич. пособие.docx, Методическое пособие для курсовой работы на конкурс.docx, Методическое пособие к Лабораторной работе №1.pdf, 208101 Учеб. пособие Физико-химические процессы в техносфере 200, Методическое пособие по МДК 02.01 (Заочнаяформа обучения).pdf, Единовременное пособие на рождение ребенка.docx, типология пособие.pdf Содержание
Видео:Действия с матрицами в ExcelСкачать  6.1. ВекторыВ
здесь i — номер компоненты вектора. Упражнение 6.1.1. Сложить два вектора:
Иллюстрация к примеру — рис. 14.
Рис. 14. Иллюстрация к упражнению 6.1.1. Задача 6.1.1 . Умножить вектор на число. Умножение вектор-столбца на вектор-строку. 1-й способ: записать в ячейку В2 формулу =$А2*В$1 и скопировать ее в остальные ячейки диапазона B2:D5. 2 -й способ (более экономный): выделить блок B2:D5. Запишем в него формулу массива . А Примечание. Если ввести формулу , то получится тот же результат, хотя с позиций матричной алгебры вектор-строку (1х3) нельзя умножать на вектор-столбец (4х1) из-за несогласованности размеров (число столбцов в первом сомножителе должно равняться числу строк во втором сомножителе). У
Примечание. Тот же результат можно получить с помощью обычной функции: =СУММПРОИЗВ (А5:А12, В5:В12). Видео:Выборка уникальных значений в Excel. #Трюк за 30 секундСкачать  6.2. Матричные операцииПростейшие операции, которые можно проделывать с матрицами: сложение (вычитание), умножение на число, перемножение, транспонирование, вычисление обратной матрицы. Упражнение 6.2.1. Сложение матриц. Задание. Сложить матрицы М и N, где Решение. 1-й способ:
Примечание. Выделен блок, имеющий те же размеры, что и исходные матрицы. Использование имен делает процедуру ввода табличной формулы намного проще:
Результат, естественно, тот же: M+N = Упражнение 6.2.2 . Вычислить линейную комбинацию матриц 2*М — N (матрицы М.и N из упражнения 6.2.1.). Решение. В блок А7:С8 ввести табличную формулу . Результат: 2*M — N = Задача 6.2.1. Осмысленные результаты (не имеющие ничего общего с матричной алгеброй) получаются при сложении матриц разных размеров. Придумать примеры и попытаться выявить правила, по которым Excel выполняет такое сложение. Д МОБР — вычисление обратной матрицы; МУМНОЖ — перемножение матриц; Примечание. Первая из этих функций возвращает число, поэтому вводится как обычная формула. Остальные функции возвращают блок ячеек, поэтому они должны вводиться как табличные формулы. У Решение. Разместить исходную матрицу в блоке А1 :СЗ.
Примечания:
Рис. 16. Иллюстрация к упражнению 6.2.3. У В блок А9:С11 ввести табличную формулу <= abs (A-AО)>.
А, введенной в формулу как массив констант: =МОПРЕД(<-73; 78; 24: Задача 6.2.2 . При каком значении элемента а33 определитель матрицы А обратится в нуль. Задача 6.2.3. Дана матрица S = Е — единичная матрица. Задача 6.2.4. Вычислить обратную матрицу для и применить форматирование, чтобы элементы матрицы представляли собой правильные дроби. Выбрать формат на основе величины определителя матрицы. Набор матричных операций в Excel беден. Если нужно серьезно работать с матрицами, лучше прибегнуть к помощи таких математических пакетов, как MatLAB (Matrix LABoratory), Mathematica, Derive . Видео:Урок 4. Формулы Excel для начинающихСкачать  Вычисление длины (модуля) вектора в EXCELhistory 14 декабря 2015 г.
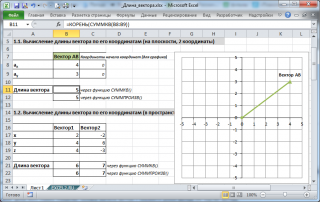
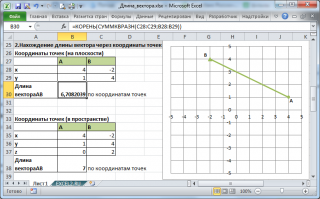
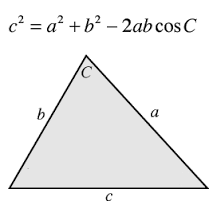
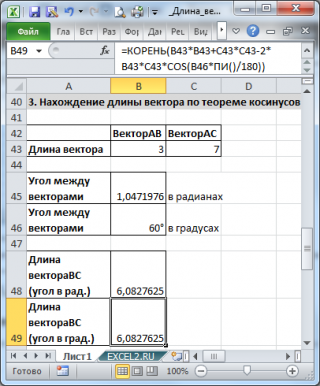
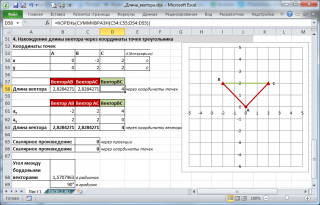
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними). Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора. Видео:Собственные значения и собственные векторыСкачать  1. Вычисление длины вектора по его координатамЕсли даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле В случае вектора в пространстве добавляется третья координата В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ). Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле = B8*B8+B9*B9 . В файле примера также вычислена длина вектора в пространстве. Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) . Видео:Математика это не ИсламСкачать  2. Нахождение длины вектора через координаты точекЕсли вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29)) В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно. Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах. По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов. Видео:Собственные векторы и собственные числа линейного оператораСкачать  3. Нахождение длины вектора по теореме косинусовЕсли требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними). Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45)) В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ). Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180)) Примечание : для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат , см. например, статью Отображение широты и долготы в MS EXCEL Видео:Как вычитать отнимать числа в ExcelСкачать  4. Нахождение длины вектора через координаты точек треугольникаПусть заданы 3 точки треугольника, образованного векторами. Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)) . Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов). Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать  5. Нахождение координат вектора через координаты точекСделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор. Видео:23 Функция ЕСЛИ в Excel (IF)Скачать  Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя)Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
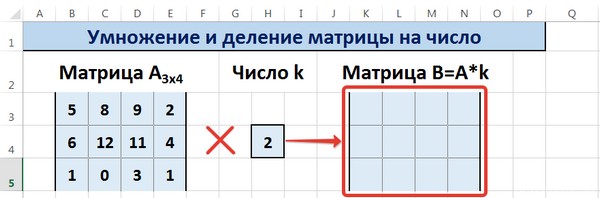
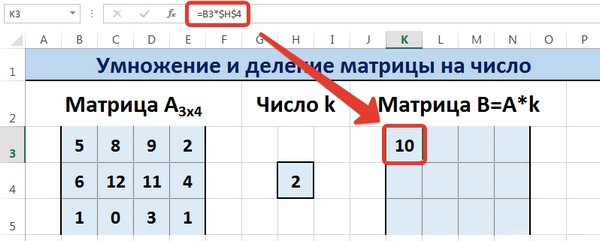
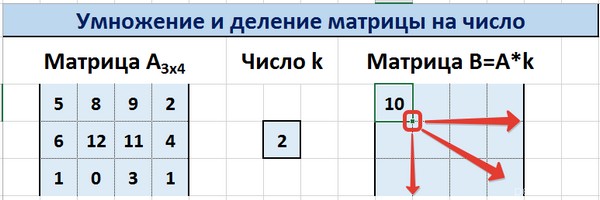
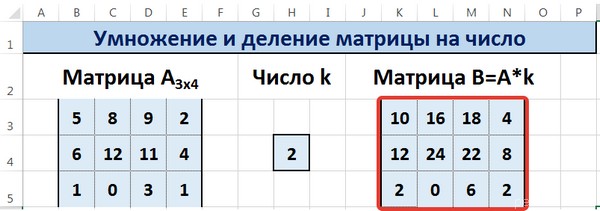
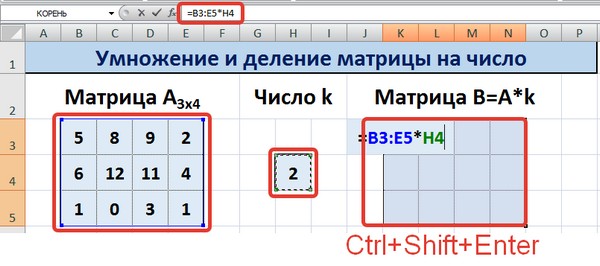
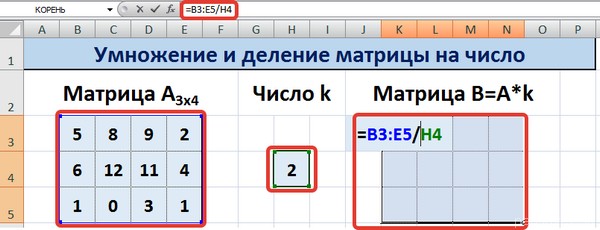
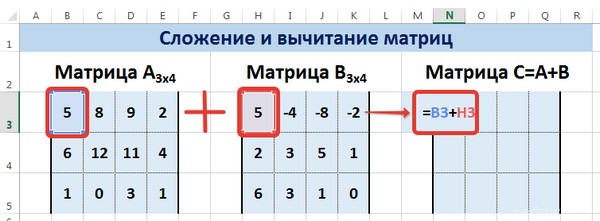
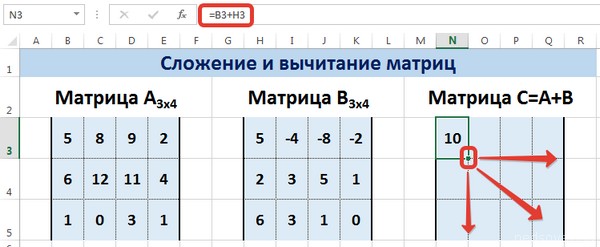
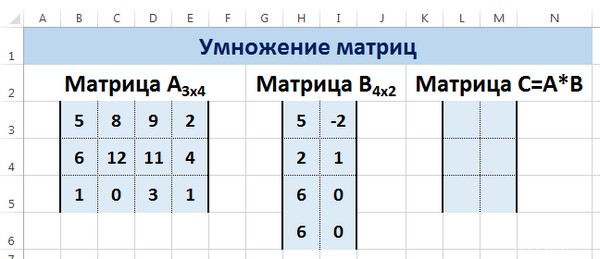
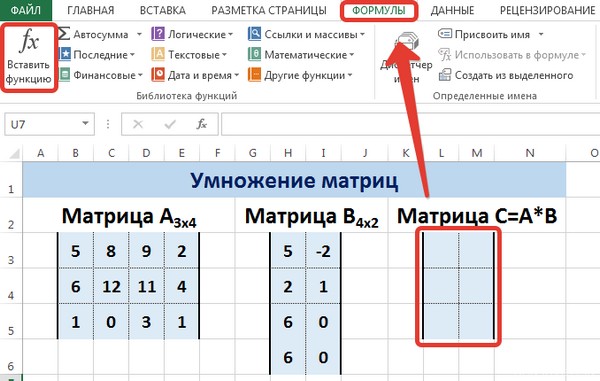
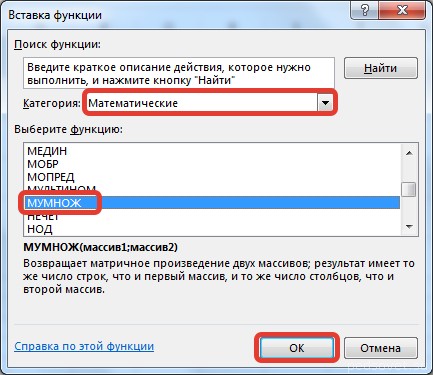
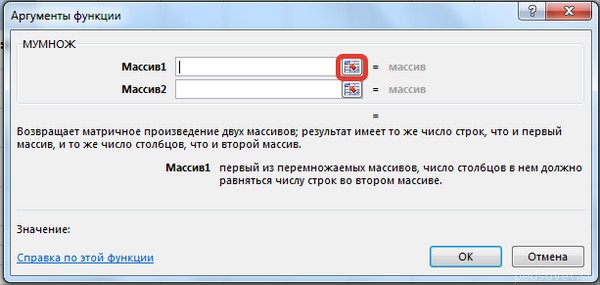
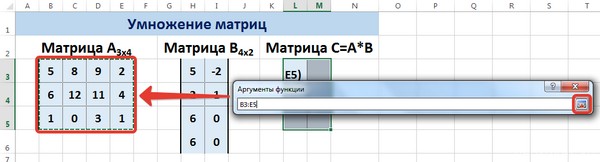
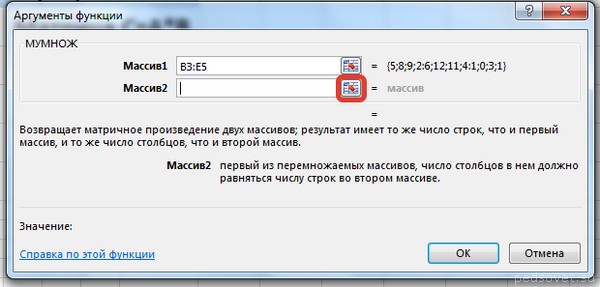
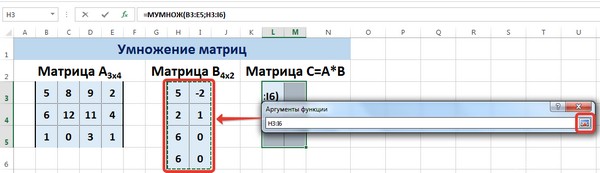
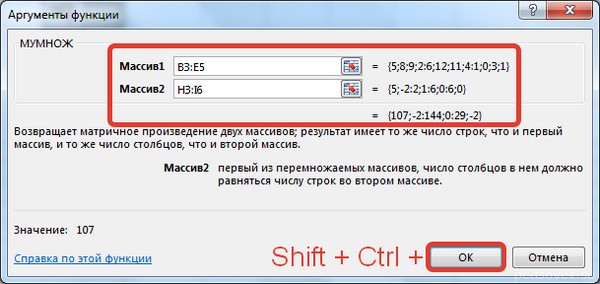
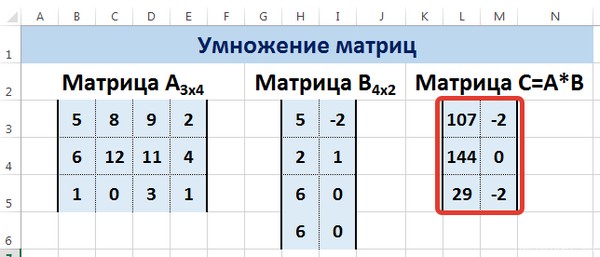
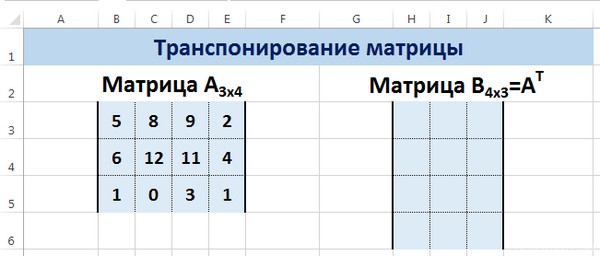
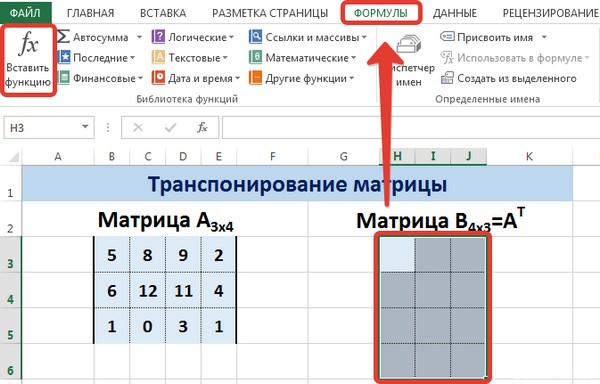
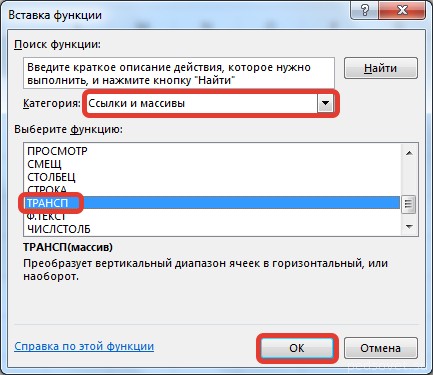
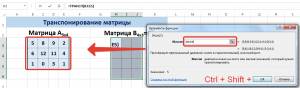
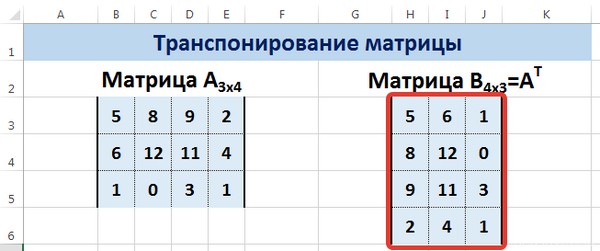
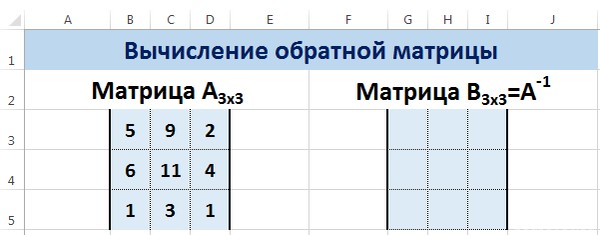
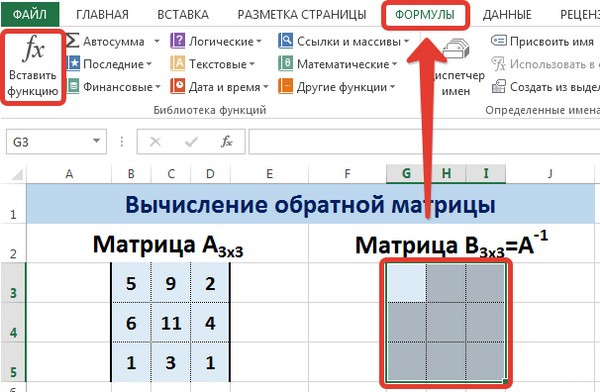
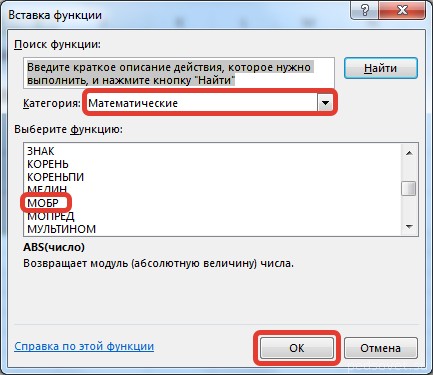
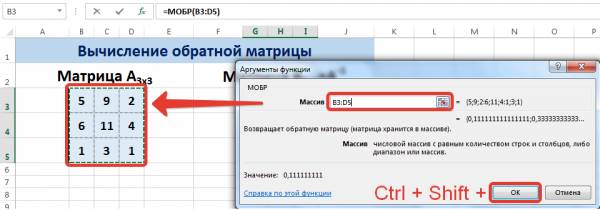
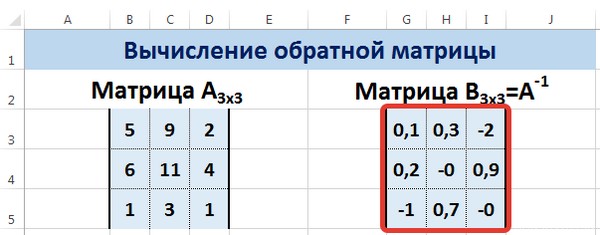
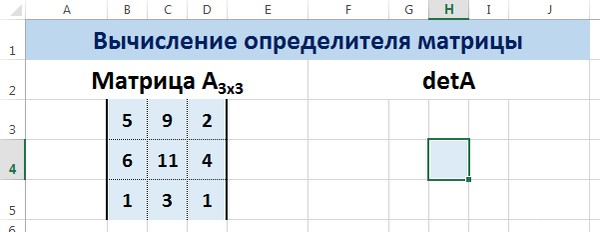
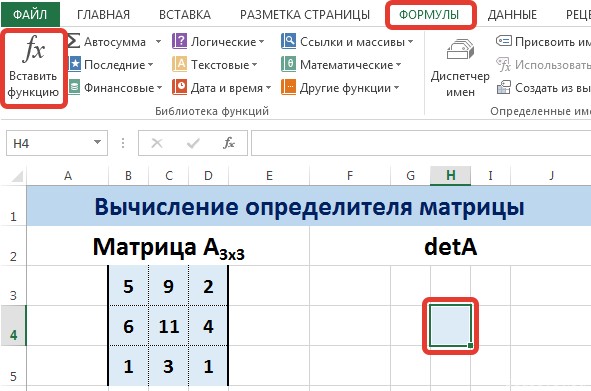
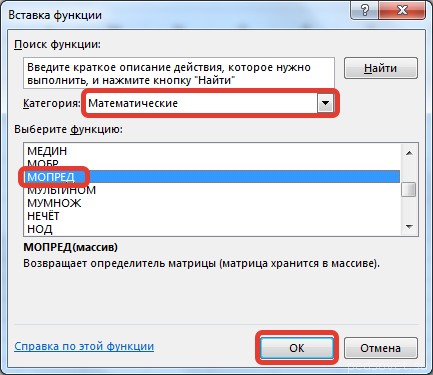
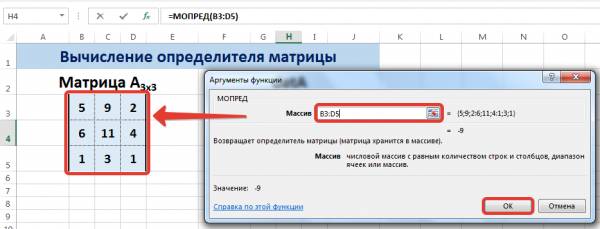
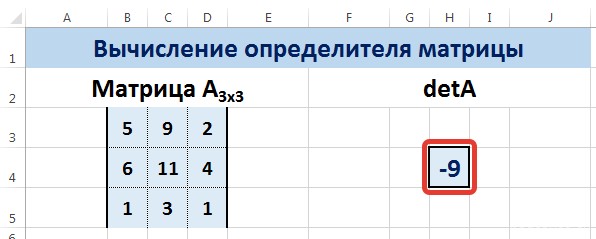
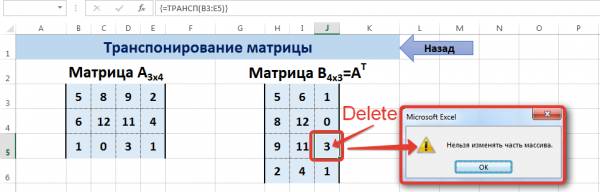
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы. Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать  Умножение и деление матрицы на число в ExcelСпособ 1Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k. Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А. Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась. С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В. Таким образом, мы умножили матрицу А в Excel и получим матрицу В. Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В. Способ 2Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива. Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон. Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/». Видео:Поиск решения в ExcelСкачать  Сложение и вычитание матриц в ExcelСпособ 1Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij. Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться. С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С. Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С. Способ 2Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива. Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон. Видео:Excel. Подсчёт уникальных значений. Подсчёт повторяющихся значений.Скачать  Умножение матриц в ExcelСледует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В. Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2. Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию. В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК. В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке. Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке. Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2. Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке. В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК. ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С. Мы получим результат умножения матриц А и В. Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически. Видео:Простой подсчет количества символов в ячейках Excel. #ТрюкиExcelСкачать  Транспонирование матрицы в ExcelТранспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т . Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3. Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы. На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК. В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК. ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т . Нажмите для увеличения Мы получили транспонированную матрицу. Видео:как добыть корень в ExcelСкачать  Нахождение обратной матрицы в ExcelМатрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов). Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР(). Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию. В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК. В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК. ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 . Нажмите для увеличения Мы получили обратную матрицу. Видео:Решение системы уравнений в ExcelСкачать  Нахождение определителя матрицы в ExcelОпределитель матрицы — это число, которое является важной характеристикой квадратной матрицы. Как найти определить матрицы в ExcelПусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД(). Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию. В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК. В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК. Нажмите для увеличения Мы вычислили определитель матрицы А. В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива. Нажмите для увеличения Мы можем удалить только все элементы этой матрицы. Видео:Excel: если ячейка содержит определенный текст, то..(найти и задать условие) Если есть искомые словаСкачать  ВидеоурокКратко об авторе:
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя 📺 ВидеоСобственные значения и собственные векторы матрицы (4)Скачать  1 Функция СУММЕСЛИ в excel (SUMIF)Скачать  Как разложить вектор по базису - bezbotvyСкачать  Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать  |

 екторы — это наборы чисел, расположенные горизонтально (вектор-строка) или вертикально (вектор-столбец).
екторы — это наборы чисел, расположенные горизонтально (вектор-строка) или вертикально (вектор-столбец). 1
1 В блоке (вектор-столбце) А2:А5 записаны числа: 1,2,3,4. Требуется получить в блоке B2:D5 три вектор-столбца, каждый из которых представляет собой результат умножения исходного вектор-столбца на вектор-строку: 2, -3, 4 (B1:D1). Рис.15. К упр. 6.1.2.
В блоке (вектор-столбце) А2:А5 записаны числа: 1,2,3,4. Требуется получить в блоке B2:D5 три вектор-столбца, каждый из которых представляет собой результат умножения исходного вектор-столбца на вектор-строку: 2, -3, 4 (B1:D1). Рис.15. К упр. 6.1.2. нализ решения. Табличный массив — вектор-строка, а блок А2:А5 — вектор-столбец. Значит, матрица B2:D5 размерностью 4Х3 является результатом умножения вектор-столбца А2:А5 (4Х1) на вектор-строку B1:D1 (1Х3).
нализ решения. Табличный массив — вектор-строка, а блок А2:А5 — вектор-столбец. Значит, матрица B2:D5 размерностью 4Х3 является результатом умножения вектор-столбца А2:А5 (4Х1) на вектор-строку B1:D1 (1Х3).

 становить курсор в ячейку, где нужен результат.
становить курсор в ячейку, где нужен результат.
 и N=
и N= 



 ля матричных операций в Excel предусмотрены функции, входящие в категорию «Математические»:
ля матричных операций в Excel предусмотрены функции, входящие в категорию «Математические»: пражнение 6.2.3. Вычислить определитель и обратную матрицу для матрицы:
пражнение 6.2.3. Вычислить определитель и обратную матрицу для матрицы: ак и следовало ожидать, получилась матрица, близкая к единичной.
ак и следовало ожидать, получилась матрица, близкая к единичной.


 . Вычислить матрицу 2SS Т — Е, где Т — операция транспонирования,
. Вычислить матрицу 2SS Т — Е, где Т — операция транспонирования,

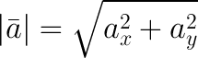
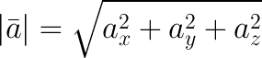
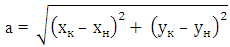

 Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.
Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.