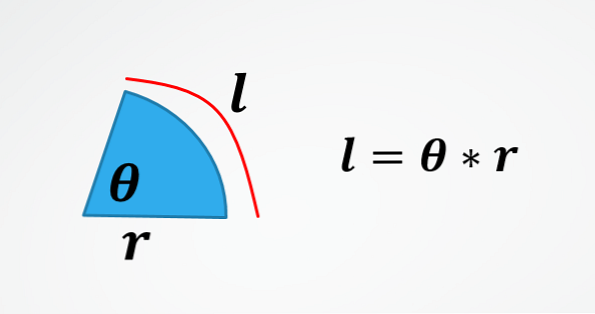Как вычислить смещение окружности (5 видео)

Формулы углового смещения и решаемые упражнения

угловое смещение оно генерируется, когда объект движется по пути или траектории, имеющей форму круга. Это отличается от смещения; в то время как угловое смещение измеряет пройденный угол, смещение измеряет расстояние.

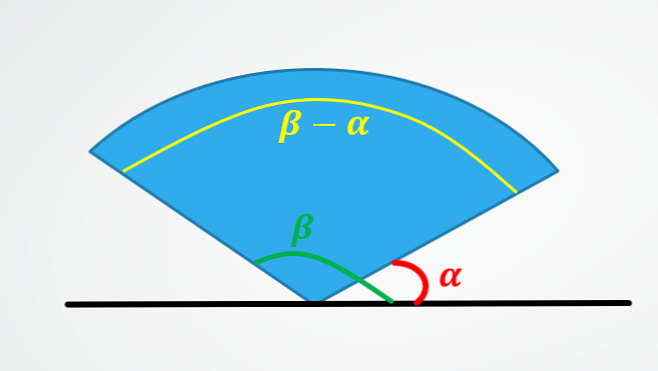
Для расчета углового смещения объекта, который движется по окружности, можно использовать два пути: если известен начальный и конечный угол, то угловое смещение будет вычитанием между конечным углом и начальным углом..

Если длина смещения (длина окружной дуги в пути) и радиус окружности известны, то угловое смещение определяется как θ = l / r..

1 формулы
2 упражнения
- 2.1 Первое упражнение
- 2.2 Второе упражнение
- 2.3 Третье упражнение
3 Ссылки

Содержание

формулы
обучение
Первое упражнение
Второе упражнение
Третье упражнение
Всё про окружность и круг
Движение по окружности
Угловая скорость
Нормальное ускорение
Тангенциальное ускорение
💥 Видео

Видео:Длина окружности. Математика 6 класс.Скачать

формулы

Для получения формул, описанных выше, вы можете увидеть следующие изображения:

Первый показывает, почему угловое смещение равно вычитанию конечного угла минус начальный угол.

На втором изображении формула для длины дуги окружности. Поэтому, очистив θ, вы получите формулу, описанную в начале.

Видео:Уравнение окружности (1)Скачать

обучение

Ниже приведены некоторые упражнения, в которых следует применять определение углового смещения и где используются формулы, описанные выше..

Первое упражнение

Хуан пробежал дистанцию 35 метров по круговой беговой дорожке, радиус которой равен 7 метрам. Рассчитайте угловое смещение, которое совершил Хуан.

решение

Поскольку расстояние пройденной дуги и радиус окружности известны, вторая формула может быть применена для определения углового смещения, сделанного Хуаном. Используя формулу, описанную выше, получаем, что θ = 35/7 = 5 радиан.

Второе упражнение

Если у вас есть то, что Марио проехал на своем автомобиле половину круговой гоночной трассы, каково угловое смещение, которое сделал Марио??

решение

В этом упражнении будет применена первая формула. Поскольку известно, что Марио прошел половину пути, можно предположить, что он начал гонку под углом 0 °, а когда он достиг середины круга, он прошел 180 °. Поэтому ответ 180 ° -0 ° = 180 ° = π радиан.

Третье упражнение

Мария имеет круглый бассейн. Ваша собака бегает по бассейну на расстоянии 18 метров. Если радиус бассейна составляет 3 метра, каково угловое смещение талисмана Марии??

решение

Поскольку пул является круглым и вы знаете его радиус, вы можете перейти ко второй формуле.

Известно, что радиус равен 3 метрам, а расстояние, пройденное домашним животным, равно 18 метрам. Следовательно, выполняемое угловое смещение равно θ = 18/3 = 6 радиан.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω